
Gauss's Law for Electric Fields
1. Mathematical Background
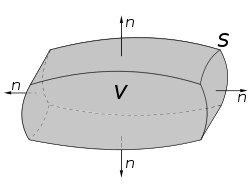
The Divergence Theorem, which states that for any compact space 




2. What is Gauss's Law?
Maxwell's equations are fundamental results that govern the behavior of - and interactions betewen- electric and magnetic fields. We see how Maxwell's equations arise from a few simple physical principles coupled with the vector analysis.
If 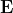
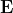


where the integral is held over the surface 

where 

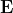

&space;=&space;\frac{q}{4\pi&space;\epsilon_0}&space;\frac{\mathbf{x}}{\lVert&space;\mathbf{x}&space;\rVert^3})
where 


2-1. Surface that does not enclose origin
For the electric field defined above, we can easily verify that
^{-3/2}&space;-&space;3x^2&space;(x^2&space;+&space;y^2&space;+&space;z^2)^{-5/2}&space;=&space;0)
wherever the field is defined. So if
 does not contain origin, then automatically flux is zero.
does not contain origin, then automatically flux is zero.
2-2. Surface that does enclose origin

Now the question is, how do we calculate the flux of the electric field across surfaces that do enclose the origin? The trick is to find an appropriate way to exclude the origin from consideration. To that end, first suppose that the surface 
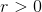

Then the outward unit normal to 

Now using original equation,
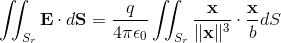
Since 
&space;=&space;\frac{q}{\epsilon_0}&space;\end{align*})
Now, suppose 












so that

3. What about multiple charges?
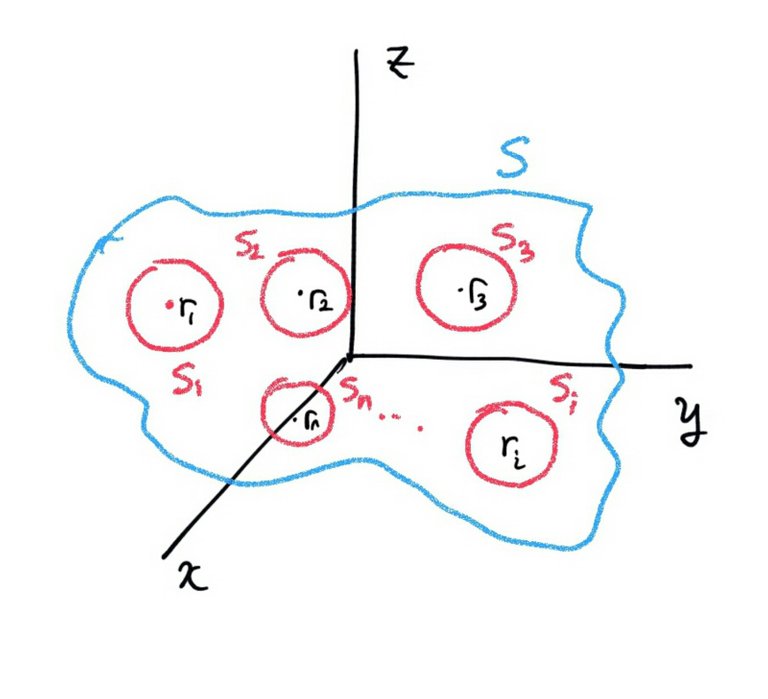
Wel,, suppose a point charge of 

&space;=&space;\frac{1}{4\pi&space;\epsilon_0}&space;\sum_{i=1}^{n}&space;q_i&space;\frac{\mathbf{x}&space;-&space;\mathbf{r}_i}{\lVert&space;\mathbf{x}&space;-&space;\mathbf{r}_i&space;\rVert^3})
Since the electric field is just linear sum of each electric fields generated by point charges, 
)

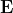


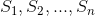


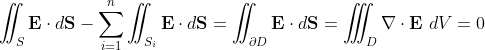
And using the Gauss's Law for single charge,
4. What about continuous charge Distribution?

Finally, consider the case not of an electric field determined by discrete point charges, but rather of one determined by a continuous charge distribution given by a charge density )

&space;dV)
so that, we have
&space;=&space;\frac{1}{4\pi&space;\epsilon_0}&space;\iiint_{D}&space;\rho(\mathbf{x})&space;\frac{\mathbf{r}&space;-&space;\mathbf{x}}{\lVert&space;\mathbf{r}&space;-&space;\mathbf{x}&space;\rVert^3}\&space;dV)
Now the question arises. Does this integral converges at points 
&space;\neq&space;0)
4-1. Proof of Convergence.
First write )
&space;=&space;\frac{1}{4\pi&space;\epsilon_0}&space;\left(&space;\iiint_{D}&space;\rho&space;\frac{r_1&space;-&space;x}{\lVert&space;\mathbf{r}&space;-&space;\mathbf{x}&space;\rVert^3}\&space;dV,&space;\iiint_{D}&space;\rho&space;\frac{r_2&space;-&space;y}{\lVert&space;\mathbf{r}&space;-&space;\mathbf{x}&space;\rVert^3}\&space;dV,&space;\iiint_{D}&space;\rho&space;\frac{r_3&space;-&space;z}{\lVert&space;\mathbf{r}&space;-&space;\mathbf{x}&space;\rVert^3}\&space;dV\right&space;))
where ,\&space;\mathbf{x}&space;=&space;(x,y,z))
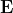
&space;\right|&space;\leq&space;\frac{|\rho|}{4\pi\epsilon_0}&space;\cdot&space;\frac{1}{\lVert&space;\mathbf{r}&space;-&space;\mathbf{x}&space;\rVert^2}&space;\leq&space;\frac{K}{\lVert&space;\mathbf{r}&space;-&space;\mathbf{x}&space;\rVert^2})
for some constant 



Now we transform cartesian coordinate to spherical coordinate. Then

because the integrand is continuous function over bounded region. Other coordinates 
4-2. Back to the formulation.
Now the intergral form of Gauss's Law, analogous to that of formula for discrete charge distribution is then
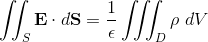
by Divergence theorem,

Now we get the differential form of Gauss's Law,
5. So why is it useful?
It can be applied to
Any closed surface
Furthermore, we only have to consider the total charge enclosed by the surface (without calculating the charges or charge distributions in the total region!)


Hello, @ mathsolver, how are you? Very interesting your article related to the Law of Gauss. I keep following your publications. Reviewed and voted.