The intermediate axis theorem is the idea that an object with three, different principle axes of rotation has an unstable intermediate axis. Take for instance, a phone. 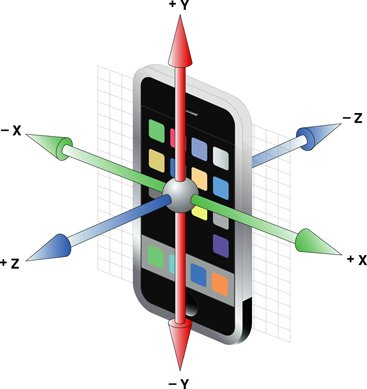
As we can see here, the phone has three principal axes of rotation. These are the three ways a phone will rotate, and we can make them rotate by meeting their moment of inertia, which is a measurement for how much energy it takes to make the phone rotate. So, the axes of the rotation that has the most mass, closest to the axes has the lowest moment of inertia, and is the strongest axes, which we can assume is Y. The axes with the least mass closest to it, requires the most energy to move, so we know that it has the highest moment of inertia, and that it is the weakest axes of rotation. We can assume it is Z.
And now we can move on to the interesting part of this whole thing, the intermediate axis. The whole purpose of this theorem is to state that the intermediate axis is unstable, which it is. The phone, when rotated on this axes (X), cannot maintain purely that rotation. Instead, it dips into the lower energy state, the lower moment of inertia, and rotates on the Y axis as well.
You can test this fairly easily yourself! Just pull out your phone, and try to spin it on those axes. The Y and Z axes stay stable and rotate along just those, but when you try flipping the phone over the X axes, it simply can't stay stable in that rotation. This causes a little flip while its in the air.
This effect can be seen here
