Zeno of Elea (490-430 BC) is a Greek philosopher who was part of the Eleatic School founded by Parmenides of Elea (501-470 BC). He is most famous for his paradoxes with which he aims to disprove the concept of motion. They were written down by Aristotle in his Physics and the three most famous of these paradoxes are the ones of Achilles and the tortoise, the Dichtonomy and an arrow in flight.

(img source: https://www.euston96.com/zenon-de-elea/)
Achilles and the tortoise
In this thinking experiment one has to imagine Achilles, a strong soldier, racing a turtoise. The turtoise has a head start against Achilles. Achilles starts running and he is a lot faster than the tortoise. But when he finally raches the point where the tortoise started the tortoise already crossed another distance. Achilles continues to run for another period of time and reaches the point where the tortoise stood last time. But the tortoise also crossed a small distance during this period of time. And this cycle continues ad infinitum. With this logic the way faster runner Achilles can never reach the tortoise. Because our everyday experience tells us that this can not be the case this is a paradox. Zeno of Elea used this as one example that should support his thesis that all motion is just an illusion and that motion itself doesn‘t exist. This is the radical opposite of another hypothesis proposed during his time by the Greek philosopher Heraclitus ( 535-475 BC) who said “everything flows“ by which he meant that everything is in a constant state of change.
His fundamental error while constructing this “proof“ is that he assumed that just because the distance would always be an infinetly small distance the total distance can not be a finite number. Although this infinetly small distance would be added up an infinite amount of times and would never be zero it is false to assume that the sum is infinite too.
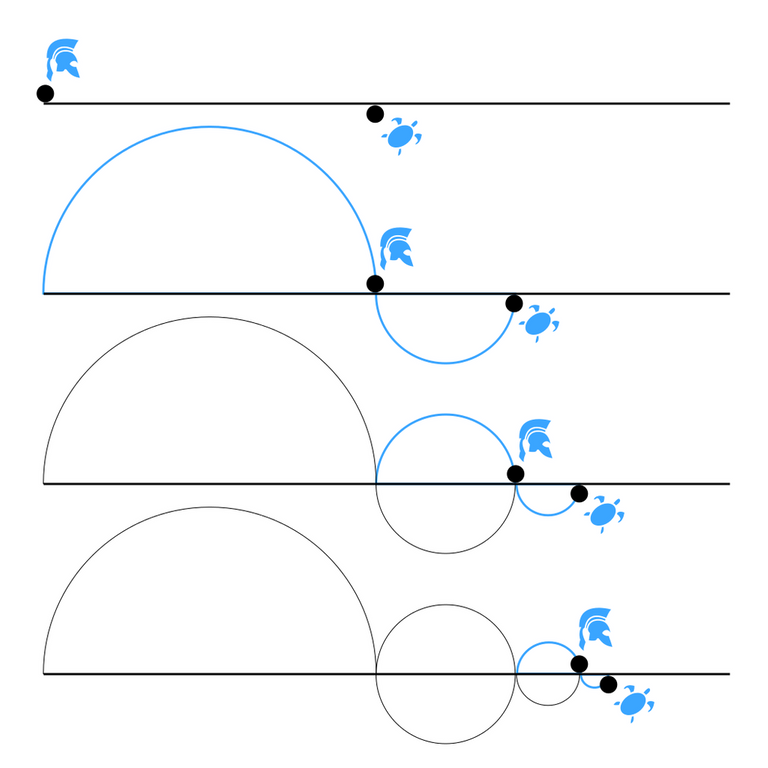
(img source : https://en.wikipedia.org/wiki/Zeno%27s_paradoxes#Achilles_and_the_tortoise , created by Martin Grandjehan for Wikipedia)
The mathematical approach
If we take a look at this problem from a mathematical standpoint we can write the total distance as a sum. Let‘s say that the tortoise has a head start of 50m and Achilles has double the speed of the tortoise. The first distance between the two would be 50m, the second would be 25m, the third would be 12,5m and so on. The sum would look as following:
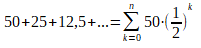
On the right side we can see the mathematically rigorous way of writing down a sum like this. As we see from the last term of the series 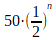 the distance between Achilles and the tortoise will get smaller and smaller the closer n gets to infinity but it never reaches zero. Zeno assumed that because of this if we let n go to infinity the whole sum would go towards infinity. But in mathematics we can prove that sums of this particular form always have a finite value if n goes towards infinity. This sum is one example of a so called geometric series, the general rule of how to calculate a series like this is:
the distance between Achilles and the tortoise will get smaller and smaller the closer n gets to infinity but it never reaches zero. Zeno assumed that because of this if we let n go to infinity the whole sum would go towards infinity. But in mathematics we can prove that sums of this particular form always have a finite value if n goes towards infinity. This sum is one example of a so called geometric series, the general rule of how to calculate a series like this is:

This means that if n goes towards infinity you will get a finite number for every -1 < q < 1 because when -1 < q < 1 then  goes toward zero because it always gets smaller and smaller:
goes toward zero because it always gets smaller and smaller:
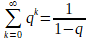
When we examine our initial series we can see that we can put the 50 in front of the series beacause it is just a constant factor and we are left with a constant factor multiplied with a geometric series where q equals 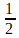 . This means that our series equals :
. This means that our series equals :

This shows that after 100 meters Achilles would catch up with the tortoise when the tortoise has a head start of 50 meters and Achilles has twice the speed of the tortoise. But more importantly it shows that the fundamental assumption that every infinite series has an infinite value is false. The result correlates with our day to day experience and the paradox doesn‘t seem like a paradox anymore.
What the paradox teaches us
While it is based on a false assumption it is still a valueable idea that encourages critical thinking about being and change itself. We can learn from the mistakes that this philosopher made and prevent makeing the same mistakes in our thinking. Another interesting point about this paradox is that it shows that mathematics isn‘t merely a tool for the different areas of science but it is also very closely linked to philosophy and there are instances where these subjects touch.

(img source: http://blog.europeana.eu/tag/philosophy/ )
Want to read about the different branches of philosophy? Check out my last article: https://steemit.com/philosophy/@apartphilosopher/branches-of-philosophy-ii-political-philosophy

Crypto related links:
Coinbase: https://www.coinbase.com/join/5a889b233b336a0439b57b8c
( Invest 100$ and get 10$ in Bitcoin for free )
Very interesting topic, it really shows the connection between mathematics and philosophy.
Thanks for reading! This link between these two fields was one of the reasons I chose this topic.
Resteemed By @tisko
Thank you for using our service! @apartphilosopher
Click here to see how to use Tisko Bot.

Congratulations! This post has been upvoted from the communal account, @minnowsupport, by apartphilosopher from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.