약간 듣보스럽지만, 아는 사람은 알고 있을만한
’몬티홀 문제 (Monty Hall problem)’ 라는 것이 있다.

문제의 실제 주인공 몬티홀
몬티 홀 문제는 미국의 TV 게임 쇼 《Let's Make a Deal》에서 기초한 것인데,
영화 ‘21’ 에서도 등장하기도 했었다.
내용은 다음과 같다.

이를 처음 본다면, 보통의 대다수 반응은 다음과 같다.
“이런 거 이해하고 싶지 않아”
“말장난이지, 결국은 2개 중에 고르는 거니까, 확률은 50:50이지”
“확률은 확률일뿐, 수학적으로 멋지게 보일려는 것뿐 의미없다”
과연 확률은 의미없는 숫자 놀이에 불과할까?
몬티홀 문제는 수학의 관점에서 봤을 때, 조건부 확률이라고 표현한다.
조건에 따라 확률이 달라진다는 논지이다.
그게 무슨 의미가 있겠냐? 하는 분들도 있을 수 있겠지만,
실제로, 저 관점에 근거하여 저 문제를 접근하면
66%의 확률이 실제적으로 높게 정답을 맞추는 데
도움이 된다는 걸 알 수 있을 것이다.
만약, 잘 이해가 가지 않는다면,
친구와 지금 몬티홀 문제를 시험삼아, 진행해보고
바꿨을 때와 바꾸지 않았을 때를 비교해보라.
문제를 행하면 행할수록,
2번째 선택에서 답을 바꿨을 때의 분명히 정답율이 높을 것이다.
그렇다면,
정확히 왜 이런 현상이 발생하는지 알아보자.
식을 정리하자면 다음과 같지만,
(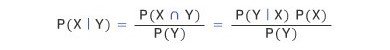 )
)
나는 수학이 범우주적인 학문이라고 생각하지만,
고리타분하게 식으로 이 글을 전개하고 싶진 않다.
대신, 훨씬 효과적인 이미지 정보 전달을 하겠다.
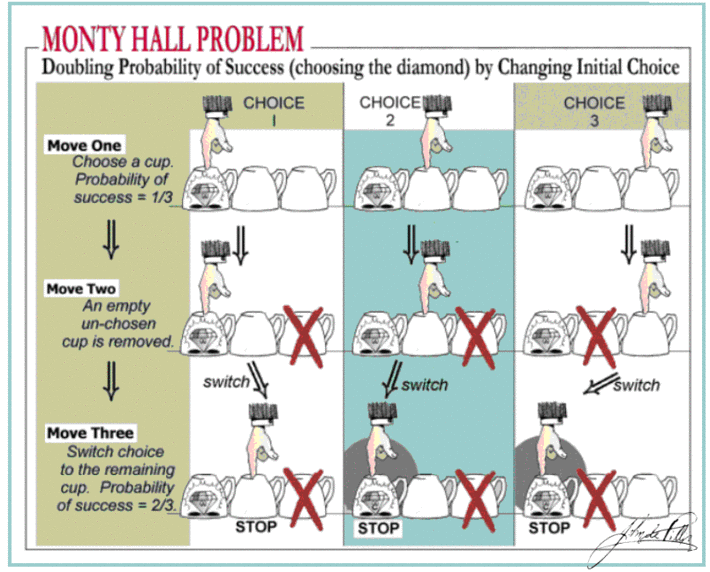
그림에서도 분명하게 드러나 있듯이,
첫번째 선택에서는 오답을 고를 확률이 더 높다.
정답을 고를 확률은 당연히 3분의 1이고 말이다.
이게 핵심 요지다.
내가 첫번째 고른 답이, 확률적으로
틀린 답일 가능성이 더 높다는 걸 깨달아야 한다.
그렇기에 하나의 변수가 제거되었을 때,
2번째 답을 옮기면, 정답율이 높아지는 것이다.
그렇다면 트레이딩에서는 어떨까?
선택지는 매수, 홀드, 매도
역시나 이익은 하나고, 손해는 2개다.
하지만 어떤 선택지를 선택해야 옳은 선택이 되는지는 아무도 모른다.
그리고 가장 중요한, 확실한 변수 제거가 없다.
변수가 확실히 오답이라고 판단할 것은
투자자의 판단 밖에는 없는 것이다.
보조적인 장치로 챠팅이 있겠지만,
누구도 시장을 정확하게 예측할 수 없다.
다만 대응하거나, 모멘텀을 읽을 뿐이다.
적어도 모멘텀을 읽을 줄 안다면,
위에서 하나의 변수를 지울 수 있는데 도움이 될 것이고,
챠트를 파악할 수 있어서, 변수를 높을 확률로 하나 걸러낼 수 있다면,
첫번째 선택에서, 반대로 가는
트레이딩 기법이 확률적으로 더 좋은 결과를 낳을 수 있다.
왜 내가 사면, 내리고! 팔면 오르냐?!
그건 트레이더의 판단력 부족이 가장 큰 원인이다.
장대 양봉이 이미 여러번 나온 상태에서 신나서 들어가거나,
거시적으로 하락장인데, 양봉이 몇번 나왔다고 해서 들어가거나,
하면 질 수 밖에 없다.
상승장을 유도하거나,
매집 후, 어느 고점 혹은 저점에서 끌어내리거나, 올리는 것은
그를 파악하지 못한 트레이더에게는 함정과도 같기 때문이다.
어떤 한 방향으로 강력하게 움직인다는 건,
그 반대 움직임 또한 빠르게 올 가능성이 매우 높은 게 트레이딩의 변동성이다.
폭락장에서 흐름에 못이겨 팔거나,
상승장에서 겁없이 매수를 하는 트레이더들에게 감히 조언을 드리고 싶다.
그 판단은 오답일 가능성이 매우 높다.
그러니, 잠시만 한번 더 생각한 후, 확실해보이는 변수를 하나 제거하고
답을 바꿔 생각해보시라.
물론 이 모든 건 확률론일 뿐이다.
절대 정답은 아니다.
하지만, 승산의 확률을 수학적으로 높이는 과정이
가치가 있다는 것을 깨닫게 된다면,
트레이딩에도 큰 도움이 될 것이라고 생각한다.
p.s
시험 5지선다를 생각하시는 분들이 있는데,
그건 조건부 확률을 접목할 여러 가지 조건들이 맞지 않는다.
3개의 변수를 확실하게 제거하는게 힘든 경우가 많으며,
정답에 유력한 답이 보이면, 변수의 공평성이 이미 흐트러지기 때문이다.