A MILLENNIUM PROBLEM
The first to substantiate the problem was the Greek mathematician Diocles, more than 2,000 years ago.
Then, for centuries, scientists like Newton or Leibniz had tried to solve the challenge: to make the vision of objects through spherical lenses not lose sharpness.
Newton invented a telescope that solved the so-called chromatic aberration (which prevents focusing the colors at a single point), but not the spherical aberration.
In the last century, in 1949, two scientists posed the dilemma in a formal article. From there, it would be known as the problem of Wasserman - Wolf.
No one had been able to solve it fully.
THE WORLDWIDE SOLUTION AND RECOGNITION
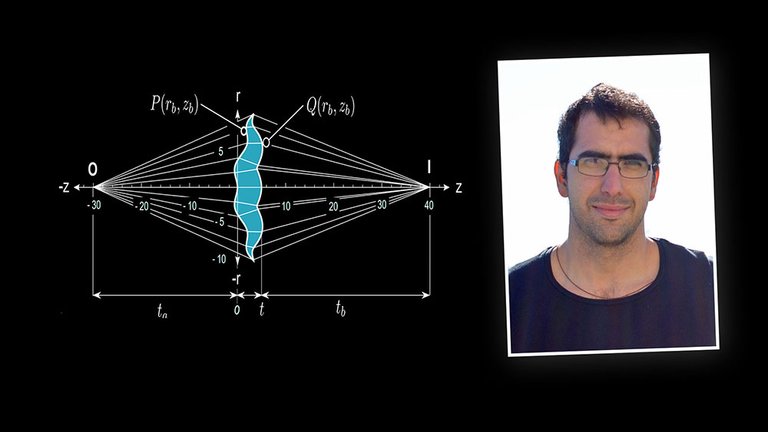
One solution to the problem was the conjunction of two lenses called non-spherical but aspheric (only spherical on part of its surface).
However, until now, the calibration of these lenses depended on a calculation not entirely accurate.
"(In contrast) the analytical solution (found by them) is accurate, by using the equation you will have the precise result no matter what the variables change," he explains.

Rafael and Alejandro published the solution in the article General formula for bi-aspheric singlet lends design free of spherical aberration, in the specialized magazine Applied Optics.
"It went very well because we had the distinction of the editor; that's very rare: less than 1 percent of the 35 thousand articles that have been published in that magazine have that distinction, "he says.
"During our study, we calculated the efficiency of 500 beams, and the average satisfaction of all the examples was 99.9999999999%."
THE IMPACT OF THE FORMULA
Julio César Gutiérrez, professor at the Tec who advises Rafael at the doctorate, considered that having solved the problem may imply improvements in the development of lenses.
"The optical design has technological applications that involve optical systems. Then the results have relevance not only theoretically but in other applications.
"Rafael is a very good student; enthusiastic and independent. He has a lot of initiative to try to solve challenging problems. "

TEC SUPPORT
With 28 years of age, 6 articles published in scientific journals -4 of them on this topic- and 3 more in review, Rafael highlighted the support he received from Tec.
He celebrated the resources of the institution, such as the support with a license of Mathematica software, which he used to perform the equations and simulations of the problem.
"However, the greatest support I had from the Tec was undoubtedly the confidence of my advisor, who encourages you to propose something and share it, even if you stay stuck," he said.
And he gives testimony of that, to be able to rest, after having been able to solve this millennial problem.
"I've been obsessed for many months," says Rafael, laughing. But you can already say: problem solved.