Ever woundered if math formulas are ever used in real life

A student asked this question on quora and upon research i found a whole lots of answers on the internet on arithmetic, a bit of trigonometry, and perhaps a bit of basic algebra, in order to do some mundane things that a calculator can do quite easily. Let's be honest, though - that's not what you're looking for, are you?(you reading this) You want to see how those extremely long and pretentious equations with messed up symbols actually do some good in the world rather than simply terrorize students. You want to see lots of Greek letters, English letters, infinity symbols, punctuation marks (!), and to see how that gibberish is actually helping with our day-to-day lives, justifying the money we're paying to our researchers, and to our math and physics professors.

I mean, take a couple examples of a Taylor series, for example.

Don’t they just look lovely?

Now, the fact is that these equations (and other forms of numerical schemes) actually allow humankind to do just about anything that has any relevance to the 21st century. But first, let us discuss the fact that your calculator has been cheating you even since you laid hands on it.

(It's relevant to your question, I swear.)

This is a picture of your run-of-the-mill scientific calculator. You may have stumbled upon such an object in your math classes, I don't know. Anyhow, this calculator can do all sorts of snazzy things. It can:

Calculate logarithms and exponents
Figure out all sorts of bizarre square roots
Compute various trigonometric functions, such as the sine function (as presented in the picture).

But this calculator also comes with a very, very dark secret, which it doesn't want you to find out.

You see, in reality, the calculator has absolutely no idea what any of those things are. Sines, logarithms, exponents… no idea whatsoever. Utterly clueless. It's been faking it the whole time, and you, the unsuspecting buyer, fell prey to its ploy.

In reality, a calculator can only do two things. It can add, and it can…

OK, I lied. It can only add.

I won't get into a lengthy discussion on how logic gates work (maybe there's a good question and answer here on Quora about that topic?), but in general a calculator (or a computer, for that matter) consists of many electronic transistors which allow it to carry out addition of binary numbers using the AND operator, and to ‘subtract’ by adding a number with its ‘opposite’ (which is obtained using the NOT operator). Multiplication and division can also be done, by using some clever manipulations of mulitple operators of the sort.

The same techniques can't be used, however, for sines and cosines, or for the odd exponent. The poor operators can only do basic arithmetic, leaving us quite stuck. If only we had some form of approximating those functions - extremely accurately - using some kind of function that only requires addition, subtraction, multiplication, and division…

And that, ladies and gentlemen, is exactly what a Taylor series does. It takes your trigonometric or exponential functions and approximates them using a polynomial (an expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents), which is a function that a calculator or a computer has no trouble with. We can also determine how accurate we want this approximation to be - we can add more and more ‘small’ values to the Taylor series in order to make its value closer to the function we're trying to approximate, but that means that it'll take the computer more time, as it needs to execute a longer set of operations. That being said, in many cases first and second order approximations are more than enough, even for some pretty complex formulas.

In other words, the Taylor series (and other power series of the sort) are the sole reason that computers are able to analyze any equation that involves trigonometry, square roots, and exponents. That means that we need it for pretty much anything which involves computational physics, including:

Predicting the weather. Aside from the fact that we require some heavy duty fluid dynamics equations (presented below) in order to create an accurate model of the weather, we need to approximate the derivatives, and that's usually done with a Taylor series.

Chemical and pharmaceutical research, and anything else that involves exponential decay (the Wikipedia article has a nice long list of applications).

Engineering software, for the purpose of designing better planes, boats (both of which are subject to fluid dynamics), structures, machines… it should go without saying that each branch of engineering comes with its own set of equations which are crucial to their respective fields.

Research and advances in physics, which have a tendency to eventually translate into useful little things like telephones and microwaves.

Note that almost all of the above examples make use of many other kinds of mathematical formulas, so in essence I've already answered the question multiple times…

Also, regarding MP3 devices: I loved Keith Fernandes’s answer below, which stated that you need a Fourier transform in order to reduce the audio wave down to its ingredient notes:

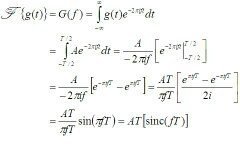
Well, in addition to that you need a Taylor series as well, since we're talking about sine waves here.

Now that you've (hopefully) been convinced of the importance of Taylor series and I've successfully upheld the honor of all nerds out there, I think I can safely say:

Q.E.D.

VOTE AND FOLLOW