Nous avons vu dans les deux derniers posts ce qu'était l'injectivité et la surjectivité au niveau des applications.
Pour rappel, une application est une relation entre deux ensembles qui a pour particularité la chose suivante : tous les éléments de départ ont une image unique.
Pour comprendre ce qui suit, il faut bien bien avoir à l'esprit les notions d'injectivité, de surjectivité et d'application (relire les anciens posts si cela n'est pas clair).
Une application bijective est une application qui est à la fois injective et surjective. Dit autrement, les éléments de l'ensemble d'arrivée admettent un seul et unique antécédent.
De façon un peu plus formelle :
Soit f, une application de E dans F. L'application est bijective si :
Pour tous y dans F, il existe un unique x dans E tel que y = f(x)
Prenons un exemple pour bien comprendre :
Soit f(x) = e^x (e à la puissance x) de R dans R+ /{0}
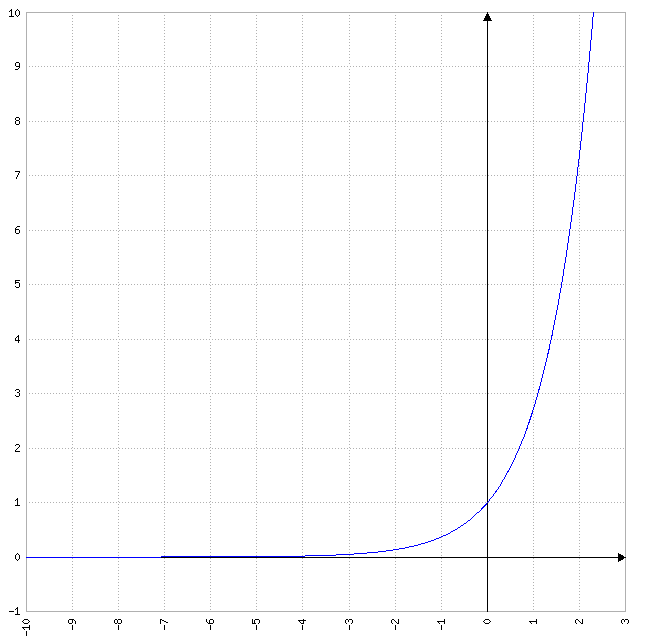
Il s'agit de la fonction exponentielle. Est-elle bijective dans ces conditions ?
Première chose, la fonction exponentielle est continue dans R+.
Ensuite, pour tous y dans R+/{0}, x = ln(y)
La fonction du logarithme népérien étant parfaitement définie dans R+/{0}, nous pouvons par conséquent trouver pour chaque y un antécédent x, ce qui nous assure la surjectivité.
De plus, trivialement, si e^x = e^x' alors x = x', ceci nous donnant l'injectivité. Ainsi, la fonction exponentielle de R dans R+ est bijective.
Si nous prenons cette même fonction de R dans R, alors nous n'avons plus la bijectivité car x = ln(y) ne fonctionne pas pour des y négatifs, empêchant la surjectivité.
Voilà qui devrait vous aider à parfaitement comprendre cette notion fondamentale et au combien importante que représente la bijectivité en mathématiques.
You got a 9.44% upvote from @upmewhale courtesy of @valuematik!
Earn 100% earning payout by delegating SP to @upmewhale. Visit http://www.upmewhale.com for details!
This post has received a 5.84 % upvote from @booster thanks to: @valuematik.
You got a 6.53% upvote from @postpromoter courtesy of @valuematik!
Want to promote your posts too? Check out the Steem Bot Tracker website for more info. If you would like to support the development of @postpromoter and the bot tracker please vote for @yabapmatt for witness!
Thanks a lot