Gabriel's Horn - The shape you could fill with paint, but could never actually paint!

How could this be true?

Gabriel's Horn is a paradox that has been confounding many a mathematician since it was first postulated by Italian physicist and mathematician Evangelista Torricelli in the 17th century.

Evangelista Torricelli - 1608-1647

Torricelli had many awesome discoveries and was widely known as the first to discover the principles behind such things as barometers. He had colleagues with famous names like Galileo and Kepler. He was an absolute intellectual rock star of his era.

It is, however, his curious thought experiment about infinities that seems to have truly stood the test of time. And, along the way, confusing many a calculus student seeking answers that come in tidy packages.

The name "Gabriel's Horn" has been used for years since its discovery as a cheeky reference to The Bible. It's crazy to think sometimes about just how entrenched religion and science were together at the time:

Come Judgment Day, it is said that Gabriel will sound a mighty horn, to announce the end is nigh. The day of reckoning is upon us. This sense of divinity is considered infinite, and the horn is the connection with finite. (source)

Biblical allegories aside, the actual mathematical principles behind "Torricelli's Trumpet" are described as follows:

He [Torricelli] discovered a mathematical figure that stretched to infinity but wasn’t infinitely big. It's shaped like a long, straight horn. So long that it never ends in a mouthpiece. It gets thinner and thinner, stretching on to infinity. But — and here’s the issue — it has finite volume. You can pour in water and even though the horn has no bottom it will get full. (source)

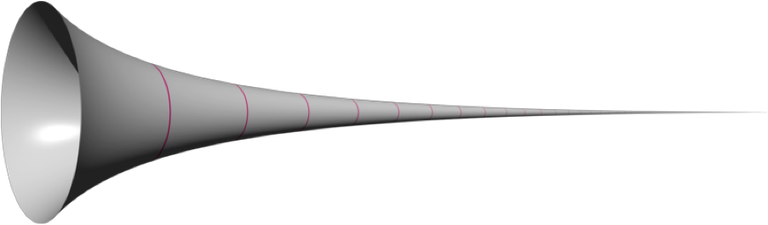
So, Torricelli, completely ahead of his time, imagined a shape that could fill completely with any substance, yet could not be encapsulated by that substance. This paradox is so weird it deserves its own explanation. Something Torricelli didn't quite have at his disposal at the time to support his hunch - Integral Calculus.

---

How This Works - Step 1: How to Find Volume

To find volume of a three dimensional shape, one convenient method is to use a bit of calculus. The procedure I am going to describe involves rotating a base region around an axis. The resulting shape is a three dimensional solid.

You have probably seen this method before with very cheap party favors, like the one illustrated below:

Once you have your three dimensional shape, you can think of it as being made up of many disks of very tiny width connected to one another. Think, a stack of coins that appears like a cylinder.

The same principle applies to curves.

To find the volume, simply find the volume of each disk first and then sum all such volumes together from the lowest endpoint a to the highest endpoint b.

This type of procedure is known as integration. Therefore, our volume formula comes from summing up infinitely many circular disks with radius r=f(x). Hence, the pi*r^2 you see present in the following integral formula.

Step 2: How to Find Surface Area

Surface area is a little more complicated to explain than the scope of this post. However, a quick study reveals that the formula comes from the idea of Papier-mâché, the practice of engulfing a shape in tiny strips of paper secured by adhesive.

Every "strip of paper" that encapsulates a three dimensional object can be thought of as being a distance f(x) away from the x-axis, with a length equivalent to:

Knowing that circumference is equal to 2*pi*radius , and summing up all our "Papier-mâché" pieces from a to b yields:

Step 3: Putting it all together

Below demonstrates the precise calculus of the Gabriel's Horn problem. Even if you are not a mathematician, note the conclusion yielded by both formulas:

How can this happen?

Well, in short, the theoretical principles behind limits and integration in Calculus drive this whole paradox. Note the emphasis on theoretical. When we performed all the calculations above, they existed only in the theoretical "everything is awesome" space of infinitesimal width and thicknesses.

In reality, if such containers were to ever be crafted, and you were to try to fill them with paint, atomic reality would clash with theoretical peculiarities.

There's no difference in surface area whether you paint the inside or outside because the surface generated has no thickness. This isn't a paradox because there are no real-life objects with no thickness which you could paint! Paint itself has finite thickness bounded by the radius of an atom, which is about 10^-10 meters. (source)

So, rest easy Steemians! Your local hardware store will not be running out of paint any time soon!

---

Image Sources:

1. Gabriel's Horn GIF - FouriestSeries
2. Evangelista Torricelli - Wikipedia
3. Gabriel's Horn Image - Wikipedia
4. Bell Demonstration - MathDemos
5. Stack of Coins - Pixabay
6. Curve 1/x - WebAssign
7. Paper Mache - Instructables

---