Hello friends of steemit, continuing with my publications referring to the science of mathematics, today I will speak in this post about the equation of the third degree or the cubic equation, all referring to their properties and I will also present some examples of how to apply this equation .
Third degree equation
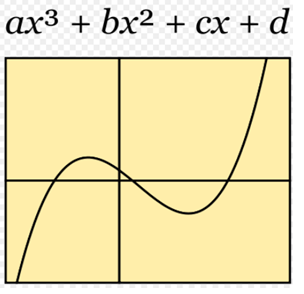
Graph of a third degree function
An algebraic equation of third degree or cubic equation with an unknown quantity is one of degree three that can be put in the canonical form:
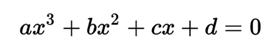
where a, b, c and d (a ≠ 0) are numbers that belong to a body, the body of real numbers or that of complex numbers, although they are often rational numbers.
Cubic Function
The cubic function is a third-degree polynomial function. It has the form:
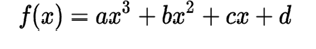
where the coefficient a is different from 0.
Both the definition domain and the image set of these functions belong to the real numbers.
The derivative of a cubic function generates a quadratic function and its integral a quartic function.
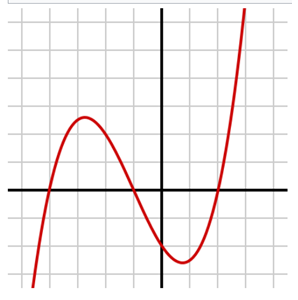
Graph of the cubic function y = 1/4 · (x + 4) · (x + 1) · (x-2) in the Cartesian plane. The roots are the places where the curve crosses the x-axis (y = 0), that is: x1 = -4, x2 = -1 and x3 = 2.
Cubic equation
The cubic equation is the equation that results from equating the cubic function to zero, and has the canonical form:
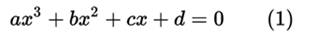
where a, b, c and d (a ≠ 0) are numbers that belong to a field, usually the field of real numbers or that of complex numbers.
Discriminating
It is important and at the same time essential to obtain elementary properties of polynomials as analysis tools in the results according to the values of their coefficients. Any cubic equation (1) with real coefficients has at least one solution x over real numbers; this is a consequence of the intermediate value theorem. We can distinguish several possible cases, using the discriminant,
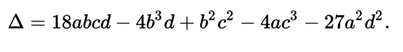
Real roots of the cubic equation
Starting from the canonical equation
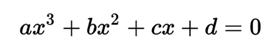
With which :
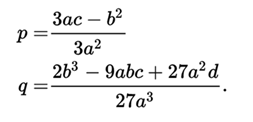
It is shown that the number of real roots depends on the discriminant of the auxiliary equation
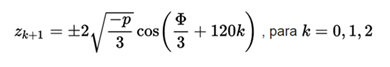
where the positive sign is used if q< 0 and the negative sign is used yes q<0. While it is given by
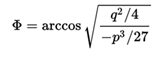
So if we want to calculate the three roots of the complete cubic equation 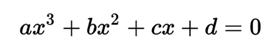 so we can easily get them as
so we can easily get them as
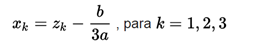
Multiple roots
In any cubic equation it is possible that multiple roots are present, that is, roots of multiplicity two and three, that is, that two or three of the roots are equal to each other. The roots of unitary multiplicity were already described before, now the double root can be presented if and only if the condition that
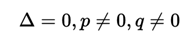
and the roots of the incomplete cubic equation will be

while the triple roots are presented when the condition that

with which the roots of the complete cubic equation will be easily calculated as

The general case
Let K be a commutative body, where roots can be extracted, property that will make it possible to solve the equation.
In an algebraically closed body it is known that every third degree polynomial (or cubic equation) has three roots. This is the case, for example, of the body of complex numbers, according to the Fundamental Theorem of Algebra.
The solution of the cubic algebraic equation was given for the first time in the book Ars Magna (from Latin, meaning 'Great Art' or 'Great Art') by the Italian mathematician Gerolamo Cardano (1501-1576) who published it in the year of 1545, which is why it is called Cardano's method.
General Formula
Given the cubic equation :
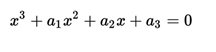
The following amounts are calculated:
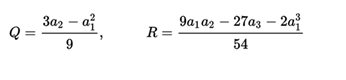
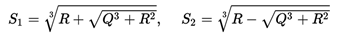
In that case the three roots can be written simply as:
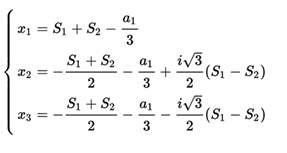
Being the discriminant 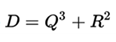 you have :
you have :
i) one of the roots is real and two of them are complex if D> 0.
ii) all roots are real and at least two are equal if D = 0.
iii) all the roots are real and different if D <0.
In the latter case the calculation of the roots is simplified a bit if the solutions are rewritten using trigonometric formulas:
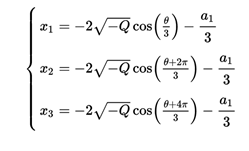
where :
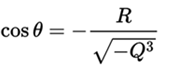
Example of an exercise applying the third degree equation

Bibliographic references:
1 . Kurosch, Course of Superior Albebra
2 . Leithold, Superior Algebra.
3 . Hall and Knigt: Superior Algebra
4 . Irving, Ronald S. (2004), Integers, Polynomials, and Rings, Springer-Verlag New York, Inc.,
5 . Cubic discriminant - Algebra
6 . demonstrated at https://web.archive.org/web/20130601171958/http://www.ecuacioncubica.com/ given that R = - q /
Wow great stuff! Are you a math or engineering major?
hello such greetings I am a student of Engineering, for me it is a pleasure to share information regarding this science so complete, greetings I hope your vote.@mindhacks
I'm still friends with you