English
In the following I would like to present a simple model, how to create own odds for sports events.
I will exemplary limit myself on one possible parameter (in this case the achieved respectively conceded goals of both teams). I will use it to calculate for example the "correct score" and "1X2" odds of a soccer game in the German "1. Bundesliga".
Lets take the game "Bayern Munich" against the "Hamburg SV" ("HSV") at the coming Saturday.
If we take a look at the current standings of the "1. Bundesliga" we can see that after 21 games Bayern Munich has scored 46 goals so far and conceded 13. The "HSV“ has scored 21 goals and conceded 37. Divided by the number of played games we get:
| average number of goals | average number of conceded goals | |
| Bayern Munich | 2.190 | 0.619 |
| HSV | 1.000 | 1.762 |
How many goals will Bayern Munich probably score? Lets take the arithmetic average between the average goals of Bayern Munich and the average conceded goals of the "HSV":
expected-goals(Bayern Munich) = (2.190 + 1.762) / 2 = 1.976
How many goals will the "HSV" probably score? Lets take the arithmetic average between the average goals of the "HSV" and the average conceded goals of Bayern Munich:
expected-goals(HSV) = (1.000 + 0.619) / 2 = 0.810
From a statistical point of view after this calculation Bayern Munich should win with a result of 1.976 against 0.81 .
Consider the home advantage!
Of course such a result is impossible. Before I explain how to convert these numbers into the probabilities of the single possible correct score results, first we still have to consider the home advantage. Lets assume that home teams in the "1. Bundesliga“ score in average 0.3 goals per game more than away teams (I let it to the reader to find out the real values :-) ). Then we can add + 0.15 to the "expected-goals(Bayern Munich)" and also subtract 0.15 from the "expected-goals(HSV)". The according to the assumed home advantage adapted result would be:
Bayern Munich - HSV = 2.126 against 0.660 .
Poisson distribution
The Poisson distribution can be used to calculate the probabilities of the different possible numbers of goals of a soccer game:
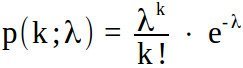
k = number of goals per team and game. λ(Bayern Munich) respectively λ(HSV) are the above calculated expected goals of both teams. In this case for example λ(Bayern München) = 2.126 und λ(HSV) = 0.660.
Example: how big would be the probability that Bayern Munich wins with 3:1?
a) To find out the probability of three goals of Bayern Munich we plug in the values k = 3 and λ(Bayern München) = 2.126 into the Poisson distribution. The result is:
p(3; 2.126) = 0.191 .
Thus the probability that Bayern Munich scores three goals is about 19 %.
b) To calculate the probability of one goal of the "HSV“ we plug in the values k = 1 and λ(HSV) = 0.660 into the Poisson distribution. The result is:
p(1; 0.660) = 0.341 . Thus the probability that the "HSV" scores one goal is about 34 %.
c) To determine the probability of the "3:1“ the single probabilities of a) and b) have to be multiplied:
p("3:1") = p(3; 2.126) ∙ p(1; 0.660) = 0.191 ∙ 0.341 = 0.065 .
Thus the probability of a 3:1 is according to this calculation method about 6.5 %.
What would be "fair odds“ to be offered for a "3:1"?
To get the odds of a result one needs the inverse value of the probability:
Odds("3:1") = 1 / 0.065 ≈ 15.
Because a bookmaker wants to make some profit he would offer odds which were significantly lower than the "fair odds" of 15 for this event ...
For example Oddsportal shows some bookmaker odds for this result.
How do I calculate the odds for a win of Bayern Munich?
Same as for the 3:1 we can now calculate the probabilities and odds for all possible single results. The sum of all probabilities of these single results where Bayern Munich is winning is the probability that Bayern Munich wins the game. "Fair odds“ for a win of Bayern Munich would be 1 divided by this probability.
How good is the presented model?
The presented model is a strongly simplified example to give a first impression of the principles of odds making. To generate odds in practice which represent the probabilities of the different possible results more exactly than the odds of bookmakers it is not good enough. My own more exact model (which of course I will not present here :-) ) calculates "fair-odds" of 24 for the 3:1 in the mentioned game (instead of 15 like this here presented model).
A more exact model can consider many more parameters than only scored and conceded goals of the teams, for example the (logarithmized) market value of the teams, the number of (conceded) chances, the shots on goal, the number of corners per game, the tendency of the last games, the strength of the previous opponents, the number of played games at home ground, the motivation of the teams (both must win, one must win, both only need a draw and so on), weather conditions (bad weather reduces the average number of goals), injuries of important players and a lot more (with as optimal as possible weighting for each parameter).
Apart from that one should be aware of the fact that even-numbered results are somewhat more probable than the Poisson distribution suggests. The reason is that if the current result in a game is for example 0:0 or 1:1 both teams risk less in average than if one team is leading by one goal, for example 1:0 or 2:1 where one team has to risk more so that the probability of another goal increases.
How to earn money using an as exact as possible prediction program?
If one manages to make odds which are more exact than the odds of bookmakers, one can exploit that: Always if any bookmaker offers odds which are higher than the own calculated „fair odds“ for an event that means that he would pay out too much in relation to the probability of the result. In these cases it should lead to a long term profit betting on such bookmaker odds ...

Image from Pixabay.
Deutsch
Im Folgenden möchte ich ein einfaches Modell präsentieren, eigene Quoten für Sportereignisse zu erstellen.
Ich werde mich beispielhaft auf einen möglichen Parameter (hier: erzielte bzw. hingenommene Tore beider Teams) beschränken, anhand dessen ich z. B. "Correct-Score-" und "1x2-Quoten" eines Fußballspiels der 1. Bundesliga festsetzen kann.
Nehmen wir das Spiel Bayern München gegen den HSV vom kommenden Samstag.
Wenn wir uns die aktuelle Bundesligatabelle nach 21 Spieltagen ansehen, so ergibt sich, dass Bayern München bisher 46 Tore erzielt hat und 13 Gegentreffer hinnehmen musste. Der HSV hat 21 Tore erzielt und 37 Gegentreffer hinnehmen müssen. Dividiert durch die Anzahl der Spieltage erhalten wir:
| durchschnittliche Toranzahl | durchschnittliche Gegentoranzahl | |
| Bayern München | 2,190 | 0,619 |
| HSV | 1,000 | 1,762 |
Wie viele Tore wird Bayern München voraussichtlich erzielen? Wir nehmen den arithmetischen Mittelwert aus dem Tordurchschnitt der Bayern und dem Gegentordurchschnitt des HSV an:
Erwartete-Tore(Bayern München) = (2,190 + 1,762) / 2 = 1,976
Wie viele Tore wird der HSV voraussichtlich erzielen? Wir nehmen den Mittelwert aus dem Tordurchschnitt des HSV und dem Gegentordurchschnitt von Bayern München an:
Erwartete-Tore(HSV) = (1,000 + 0,619) / 2 = 0,810
Bayern München müsste also statistisch gesehen nach dieser Berechnung mit 1,976 zu 0,81 gewinnen.
Man beachte den Heimvorteil!
Ein solches Ergebnis ist natürlich unmöglich. Bevor ich aber darstelle, wie man diese Werte in Wahrscheinlichkeiten für Einzelresultate umrechnet, muss zunächst noch der Heimvorteil berücksichtigt werden. Nehmen wir an, dass Heimmannschaften in der Bundesliga statistisch gesehen 0,3 Tore pro Spiel mehr als Auswärtsmanschaften erzielen (die tatsächlichen Werte zu ermitteln überlasse ich dem Leser :-) ), dann können wir zum dem von Bayern München als Heimmannschaft ermittelten Durchschnitt + 0,15 Tore hinzuaddieren und beim HSV, der Auswärtsmannschaft, 0,15 Tore abziehen. Das um den Heimvorteil ergänzte Ergebnis betrüge also
Bayern München - HSV = 2,126 zu 0,660 .
Die Poisson-Verteilung
Die Poisson-Verteilung bietet sich dazu an, die Wahrscheinlichkeiten für die verschiedenen möglichen Toranzahlen eines Fußballspiels zu bestimmen:
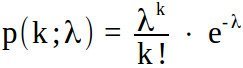
k = die Anzahl der Tore pro Team und Spiel. λ(Bayern München) bzw λ(HSV) sind die oben ermittelten erwarteten Toranzahlen beider Mannschaften. Hier wäre wäre z. B. λ(Bayern München) = 2,126 und λ(HSV) = 0,660.
Beispiel: Wie groß wäre die Wahrscheinlichkeit, dass Bayern München 3:1 gewinnt?
a) Um die Wahrscheinlichkeit für drei Bayern-Tore zu ermitteln, werden in die Formel für die Poisson-Verteilung die Werte k = 3 und λ(Bayern München) = 2,126 eingesetzt. Es ergibt sich:
p(3; 2,126) = 0,191 .
Die Wahrscheinlichkeit, dass Bayern drei Tore erzielt, beträgt also ca. 19 %.
b) Um die Wahrscheinlichkeit für ein HSV-Tor zu ermitteln, werden in die Formel für die Poisson-Verteilung die Werte k = 1 und λ(HSV) = 0,660 eingesetzt. Es ergibt sich:
p(1; 0,660) = 0,341 .
Die Wahrscheinlichkeit, dass der HSV ein Tor erzielt, beträgt also ca. 34 %.
c) Um die Wahrscheinlichkeit für das 3:1 zu bestimmen, müssen nun die beiden Einzelwahrscheinlichkeiten multipliziert werden:
p("3:1") = p(3; 2,126) ∙ p(1; 0,660) = 0,191 ∙ 0,341 = 0,065 .
Die Wahrscheinlichkeit für ein 3:1 beträgt also gemäß dieser Berechnungsmethode ca. 6,5 %.
Wie würde die "faire Quote" für ein 3:1 aussehen?
Die Quote für ein Ergebnis ergibt sich durch den Kehrwert seiner jeweiligen Wahrscheinlichkeit:
Quote("3:1") = 1 / 0,065 ≈ 15.
Da ein Buchmacher Gewinne erzielen will, würde er bei einer ermittelten „fairen Quote“ von 15 natürlich eine deutlich kleinere Quote anbieten ...
Auf Oddsportal sieht man einige tatsächliche Buchmacherquoten.
Wie berechnet man jetzt die Quote für einen Bayern Sieg?
Genauso wie das 3:1 können nun die Wahrscheinlichkeiten und Quoten aller Einzelergebnisse berechnet werden. Die Summe aller Wahrscheinlichkeiten aller Einzelergebnisse, bei denen Bayern gewinnt, entspricht dann der Wahrscheinlichkeit, dass Bayern gewinnt.
Die "faire Quote" für einen Bayernsieg ist 1 dividiert durch die Wahrscheinlichkeit, dass Bayern gewinnt.
Wie gut ist das hier vorgestellte Modell?
Es geht hier um ein sehr stark vereinfachtes Beispiel, um das Prinzip der Quotenerstellung zu verdeutlichen. Für die Praxis, um z. B. Quoten zu erstellen, die die Wahrscheinlichkeiten besser abbilden, als es die Quoten der Buchmacher tun, ist es noch viel zu ungenau. Mein eigenes, deutlich genaueres Modell, das ich hier natürlich nicht veröffentlichen werde, :-) errechnet 24 als "faire Quote" für ein 3:1 in besagtem Spiel (statt 15 wie das hier präsentierte Modell)!
Ein solches genaueres Modell kann z. B. neben den bisher erzielten und hingenommenen Toren außerdem den (logarithmierten) Marktwert der Teams, die erspielten Chancen und hingenommenen Gegenchanchen, die abgegebenen Torschüsse, die Anzahl der Eckbälle pro Spiel, den Trend der letzten Spieltage, die Stärke der bisherigen Gegner, die Anzahl der bisherigen Heimspiele, die Motivation der Teams (beide müssen gewinnen, einer muss gewinnen, beiden reicht ein Remis etc), das Wetter am Spielort (schlechtes Wetter verringert die durchschnittliche Torsumme), Verletzungen wichtiger Spieler und vieles mehr (mit jeweils möglichst optimaler Gewichtung) berücksichtigen.
Außerdem sollte man berücksichtigen, dass geradzahlige Ergebnisse häufiger sind als die Poisson-Verteilung erwarten lassen würde: Steht es z. B. 0:0 oder 1:1 ist die Risikobereitschaft der Mannschaften eher geringer als beim Stand von 1:0 oder 2:1, wo die hinten liegenden Mannschaft alles riskieren muss und deshalb die Wahrscheinlichkeit eines weiteren Tors steigt.
Wie verdient man mit einem möglichst genauen Ergebnisvorhersagemodell Geld?
Hat man es geschafft, genauere Quoten als die Buchmacher zu erstellen, lässt sich das ausnutzen:
Immer dann, wenn Buchmacherquoten höher liegen als die selbst berechnete „Faire-Quote“ bedeutet das, dass der Buchmcher in Relation zur Eintretenswahrscheinlichkeit zu viel auszahlen wird. In diesen Fällen sollte es zu einem langfristigen Gewinn führen, auf solche zu hohen Buchmacherquoten zu setzen ...
Very good article, even if chances (shots on target) are a better indicator for the strength of a team than the goals (conceded), because they happen more frequently and thus are statistically more relevant ...
!
Deine Berechnungen über die Fussballergebnisse ähneln sehr stark den Berechnungen im Risikomanagement in Unternehmen um Schadensereignisswahrscheinlichkeiten abzuschätzen. Cooler Artikel!!!
Freut mich sehr, dass dir der Artikel gefallen hat!
Weißt du @jaki01, es würde genügen, wenn du ausgeben würdest, was man wo setzen soll, Da täte ich sofort mitmachen. So fachkundige Leitung wünscht man sich beim Wetten.
Du könntest ja für mich bei den vielen Buchmachern setzen, die mich bereits auf Centbeträge runterlimitiert haben. Haha :)
ohjeee darüber kann ich au ein Lied singen von centbeträge limitiert usw...
Bin ich dabei jaki. Wie gehts jetzt weiter?
Per Private-Message. :)
ohjeee darüber kann ich au ein Lied singen von centbeträge limitiert usw...
Wow, amazing
Thanks a lot! Actually especially the beginning with the arithmetic average of the average goals of Bayern Munich and the average conceded goals of the HSV (and then reversed) to find out the probability of goals to be scored is way too simplified ... If the HSV conceeds more goals than an average team, then Bayern Munich should actually score more goals than normally and not less (intentionally I left much room for your own thoughts! :-). I just wanted to give you all an idea about how one could come from one parameter to the odds of a soccer game and I hope it was interesting. :)
Yes.. Is very good.
Good luck
soccer and maths - perfect combination, just did a post about mathematics too - happy solving @jaki01
;-) Ich mag Mathematik immer dann am liebsten, wenn sie mir Geld bringt, haha.
Aber wenn keiner deine Aufgabe löst, schaue ich sie mir vielleicht später mal an.
Aber hey, @freiheit50 ist Mathematiker, @felixxx ist "Botspezialist", lass die alle mal machen ... ich genieße jetzt erstmal meinen Tag ohne weitere Kopfarbeit, da ich erstens heute viel Zeit habe und zweitens endlich meine Grippe von letzter Woche besiegt zu sein scheint. :)
(Aber ich finde es jedenfalls super, dass du einen Mathe-Post verfasst hast!)
Das freut mich, Dein Ansatz für Mathe, Dein freier Tag und der Sieg über die Grippe, lass es krachen
great
Nice to see that you liked it! :)