
Last tutorial, I explained how the binomial expansion formula was derived, and I stated at the end of the tutorial that worked examples will be posted so as to know the advantage of the formulae.
Have you read the previous tutorial? If no, click this below link.
Deriving of binomial expansion formula for two variables (a+b)^n
Now, let's get started.
By considering this below examples,
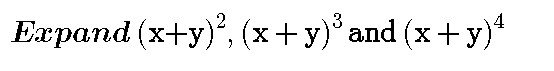
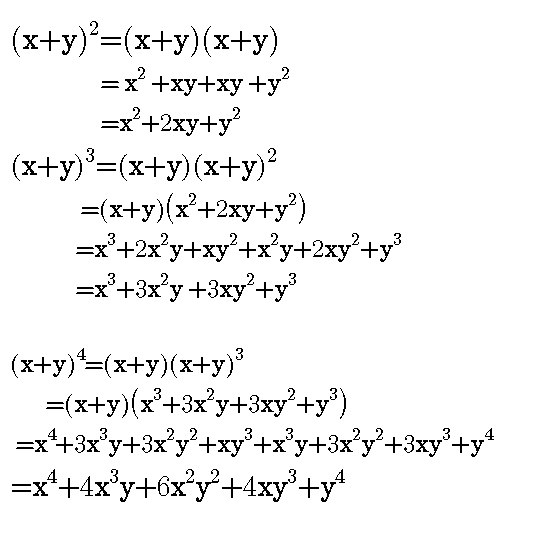
You can see that it is more complicated when we are expanding for the power of 4, let's assumes you see a contest on Steemit which the price is 2000SBD and you are given a question to expand for a power of 10 and you are given just 3minutes.
How will you do it?
Will you do it like we did in above examples?
This is where we will apply binomial expansion formula
Let's use binomial expansion formula to expand (x+y)^4 and you will know which is faster between the two methods.
Recall the formula of binomial expansion
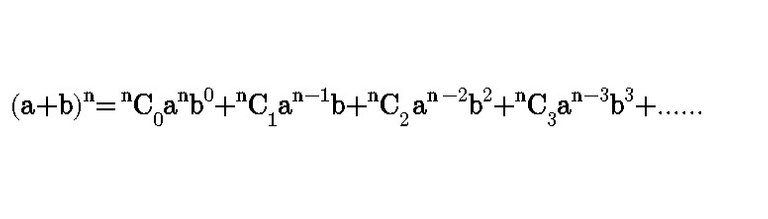
By comparing (x+y)^4 with the formula,
a=x , b=y and n=4
Substituting all the values to the formula, then we have,
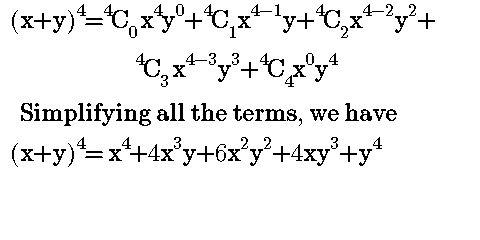
Now, which method will you apply for the contest question now?
There are some tricky questions also like expand (x - 2y)^3, the reason I bring up this kind of example is just to avoid doing mistake since we are dealing with questions with positive in all the questions that we have solved.
What we need to do is to compare it with binomial expansion formula,
a=x , b= -2y and n=3
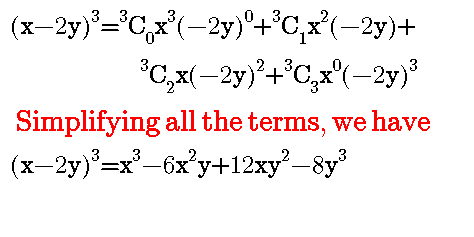
I couldn't be able to solve more examples because I'm using phone to type.
Always visit my blog for more tutorials on mathematics.
Reference
John Bird Engineering mathematics
You can also read my previous tutorials:
Deriving of binomial expansion formula for two variables (a+b)^n
Easy method to derive binomial expansion formula
Tutorial on Combination
Explanation on why 0!=1
This is very impressive. Binomial Expansion makes expansion of high power very easy either by using Combinatorial coefficients which you have explained here or using Pascal Triangle. From your work, we can deduce a very simple formula and approach in solving any expansion related to greater powers more than 2.
(a+b)^n=a^n +na^(n-1)b/1! +n(n-1)a^(n-2)b²/2! +n(n-1)(n-2)a^(n-3)b³/3! +. . . . .
Thanks for sharing 💗
Yea. That is when we simplify the combination. Thanks for reading boss.
You are very welcome 💗
Your post has been upvoted by the @steemiansarena trail. Our goal is to support minnows and help them grow. You can join our discord server
https://discord.gg/dyGGgM
Whastapp here
https://chat.whatsapp.com/50wJ8HvVsK26pKW4j2HXmS
.. You can also support us by either contributing steem or delegating SP to us
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by Hayzeed from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.