Hello everyone this is my first presentation here in this area of science, a friend told me that the sciences here in steemit are very good, and so making a reminder of my school, today I want to present this publication related to mathematics, I really like the numbers and therefore, I want to talk in this post about the analytical geometry related to the vector equation, applying addition and subtraction in sets with the vector products, in this presentation we could see some explanatory practical images, which will show step by step how to perform these mathematical procedures. Thank you for allowing me to show my knowledge here.
A vector is a portion or line segment that is directed in space, every vector is supported by a point called origin, has a length called the module that begins at the origin and ends at the end, this end is marked with an arrow marking its sense tells us which way the vector is going. The direction of the vector is the one that corresponds to the line of orientation of the segment.
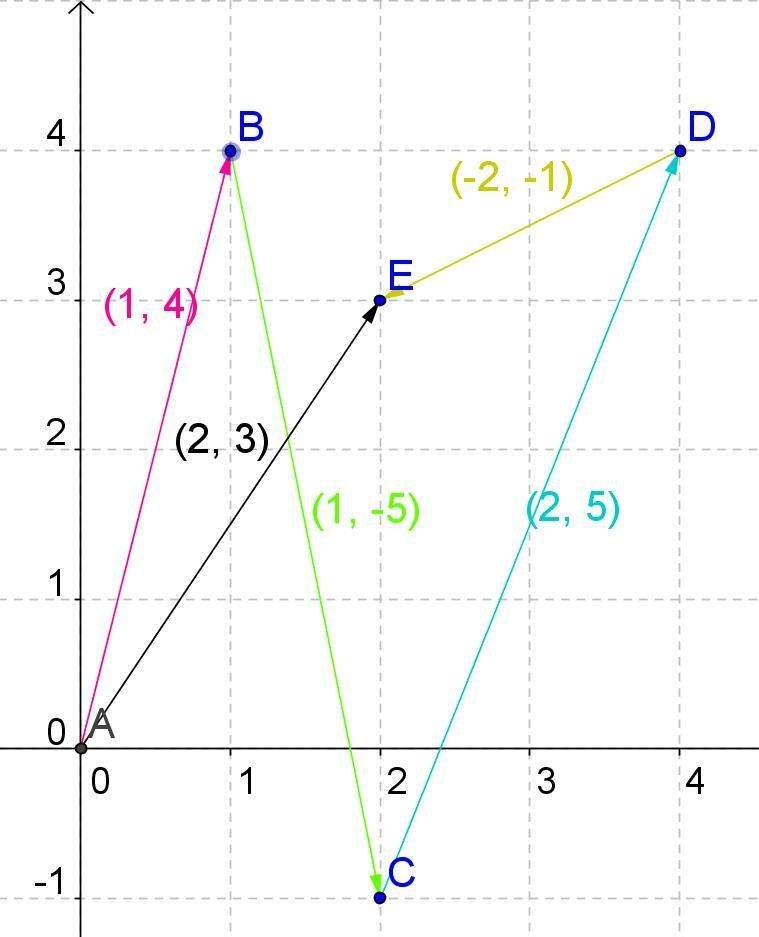
In the image we can see the sum of four vectors: to the pink vector we add the green, to this the blue and to this the yellow. In order to add them what we do is the following: from the first is placed at the end where the arrow is the second, from the second the third and so on. We have that the first pink vector has two components, those that correspond to the x axis and the y axis, one unit and four units respectively (1,4).
The second vector is placed its origin from the coordinate of this last point, we can see that the green vector has coordinates on the X axis because it goes to the right and -5 on the axis and because it goes down. In conclusion, the sum of these two vectors, red and green, would give us a vector of components or coordinates (2, -1) -not represented in the drawing.
To obtain this vector result of the sum of the two previous ones, we could join the origin of the first one that is in the coordinates 0,0 with the end of the second coordinate (2, -1). We can deduce that analytically the way to calculate it is to add the two components, those of the x: 1 + 1 and those of the y: 4+ -5. Doing the same operation with the other two vectors, we have that from the end of the green at point C we put the blue vector of components 2 and 5, that is, two units on the x axis and five units on the y axis.
Finally, on the D end of this vector we place the yellow vector, whose coordinates are both negative since the direction is to the left and down, therefore negative in the two directions of the Cartesian axes. By joining the end point E of the end of the yellow as the origin A of the pink vector, we have the black vector of coordinates (2,3), it is the result of adding all the previous vectors. We can verify that this is true if we take all the coordinates in x of the four vectors we have 1 + 1 + 2 - 2, which gives us a result of 2, if we do the same with the components on the y axis, we have 4 more -5 + 5 plus -1, which gives us a result of three, which is what the vector rises on the y-axis.

In the drawing we can see the sum of four other vectors, the pink color vector with origin in the coordinates, the green one is added, the blue one and the yellow one. If we join the E end of the yellow vector with the origin A of the first we obtain the result of adding the four vectors.
We can see that the horizontal components of the vector are negative in the case of the pink and yellow vector, since both go to the left, their units are 3 and 2, respectively.
We can also observe that the only vector that backs down is the yellow one, therefore it has in the component corresponding to the axis and a negative value, -1.
If we add the coordinates in x of the four vectors, we have that -3 + 2 + 5 plus -2 equals two.
If we add the coordinates in and we can check that 2 + 1 + 1 plus -1 equals three. These two components 2,3 are really those that correspond to the black vector that represents the sum of all the previous ones.
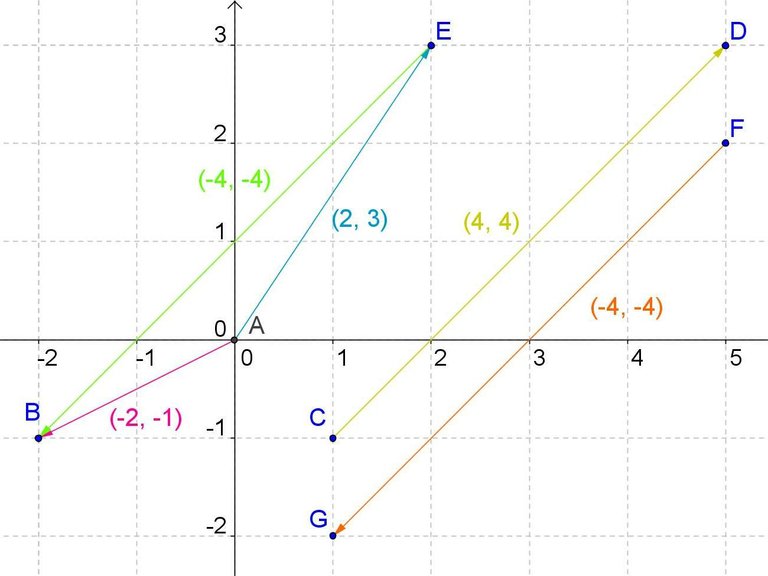
In the drawing we can see the subtraction of two vectors, the pink vector minus the blue, so we have to subtract that -2 - 2 is equal to -4 and -1 - 3 is equal to -4, the resulting vector of the subtraction of the previous two is that which has coordinates in x and y, -4, -4, respectively.
If instead of subtracting the pink vector minus the blue vector we do the opposite, the blue vector minus the pink, we have two minus -2 equals 4, while 3 minus -1 equals 4. We can see that both - drawn on the right side - have the same components but changed sign, this means that the vector formed by the components -4, -4 is directed downward and to the left, so it has the arrow of its direction thus directed, while that the yellow vector, of coordinates 4.4, is directed towards the right and upwards, because having both positive components also has its sense of orientation to the right and upwards.
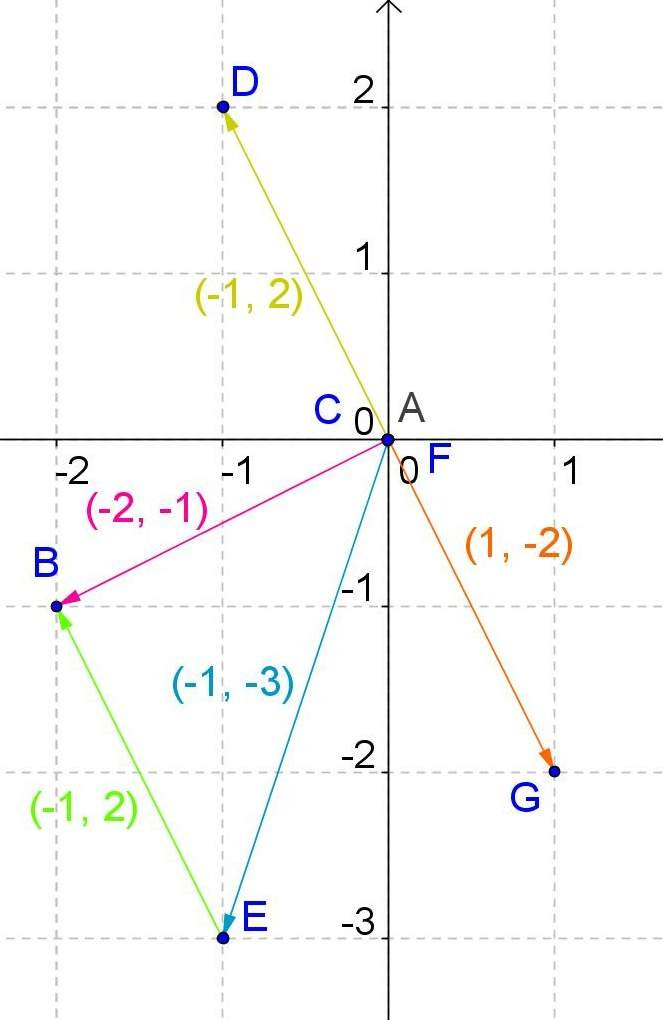
In the drawing we can see the subtraction of the pink vector minus the blue, -2 minus -1 is equal to -1 for the component in x, while -1 minus -3 is equal to 2, in its component over the y axis.
We can observe that to subtract vectors we can join their ends by means of a segment, this new vector of green color is directed to the first vector, to the vector that subtracts the second.
We can also verify that the subtraction of both vectors, the pink one minus the blue one or the other way round, generates two vectors -in yellow and in orange- with the same address but with different sense, both with the origin in the coordinates .
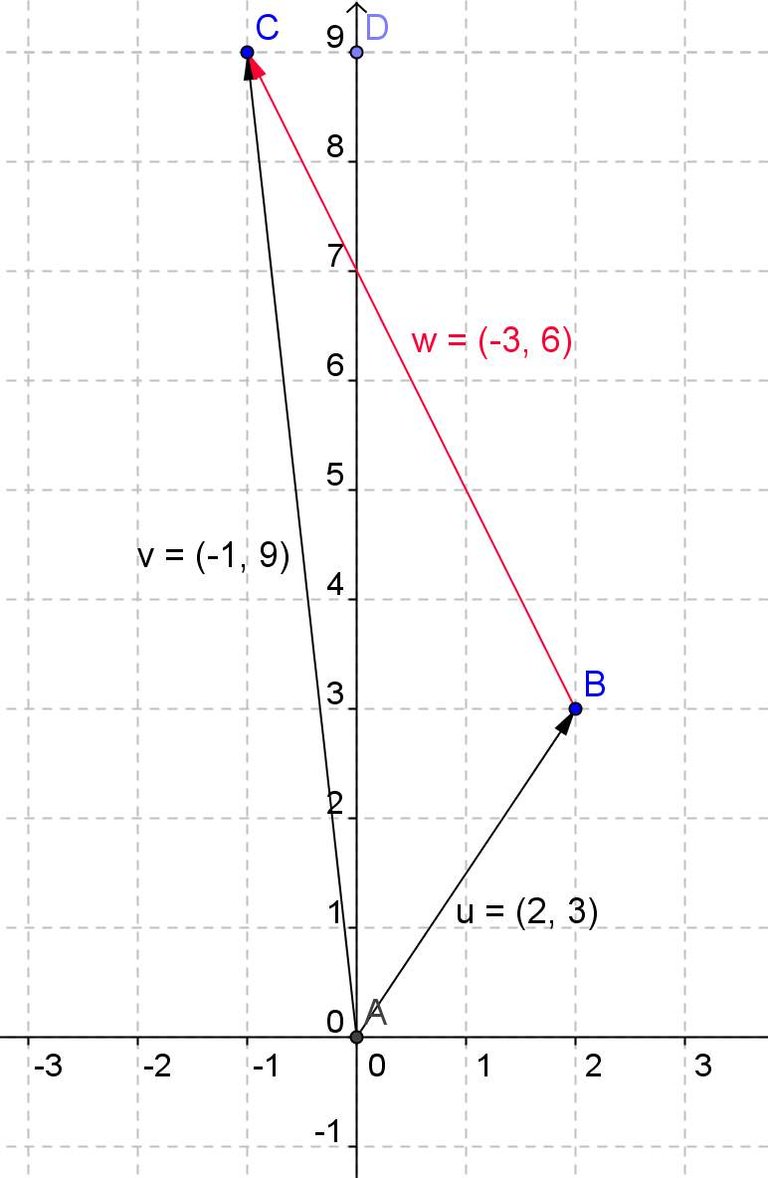
If we subtract the vector v minus the vector u we have the vector w (in red color) whose components are -3.6.
It is the result of subtracting the v of components -1,9 and the u of components 2,3.
v-u -1-2 = -3 and 9-3 = 6
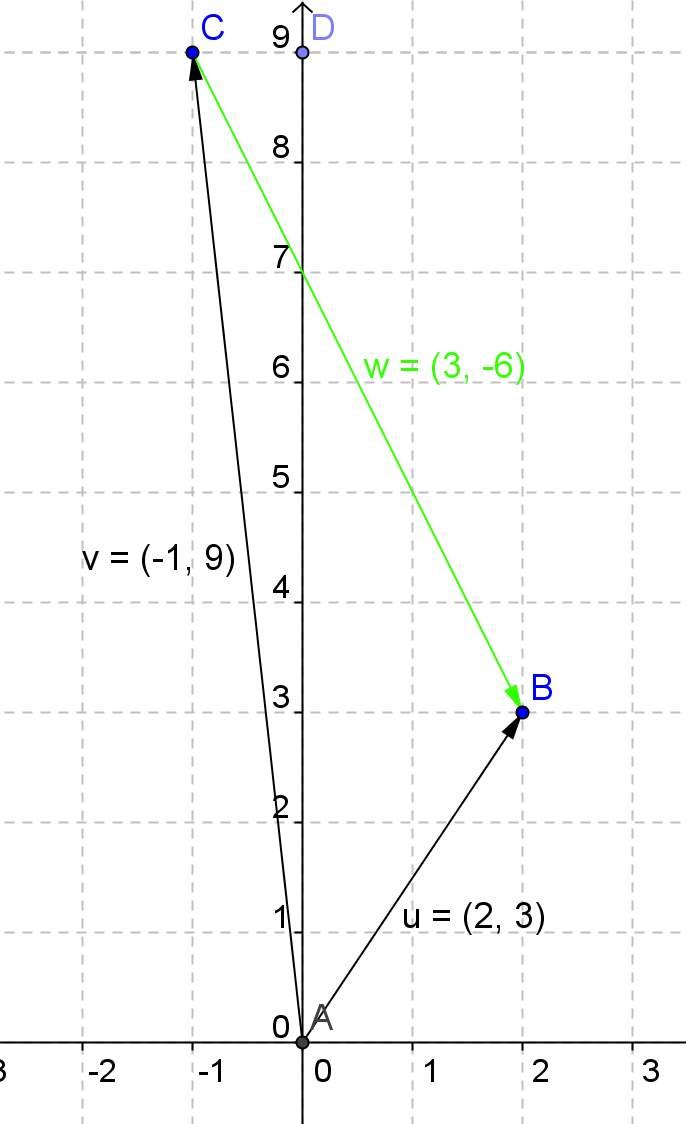
If we subtract the rector u minus the vector u, we have that its components are 3, -6
It is the result of subtracting the u of components 2,3 and the v of components -1,9.
u-v 2--1 = 3 and 3-9 = -6
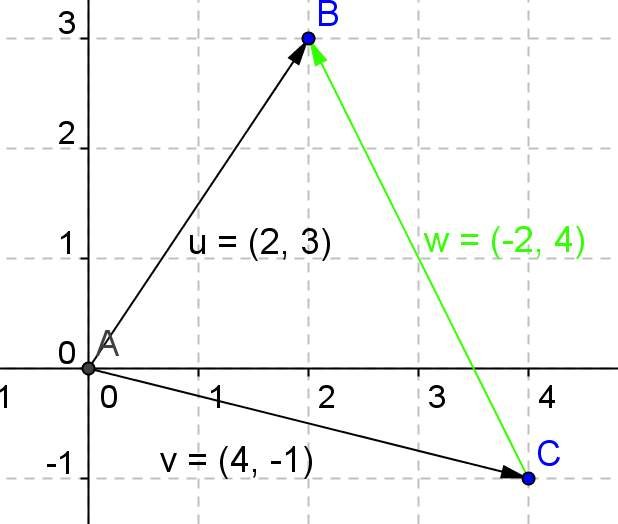
In the image we can see another example of uv vector differences, subtracting the coordinates in x from the first minus the coordinates of the second and then the coordinates in y of the first minus the second we have the difference: 2-4 = -2 3--1 = 4
-2,4 are the components of the vector v, result of the difference of u less v
To represent the vector we have that its component in x goes to the left, so it is negative, while its component in and goes up, so it is positive.
Bibliography :
- http://tutorial.math.lamar.edu/Classes/CalcIII/EqnsOfLines.aspx
- https://www.sangakoo.com/en/unit/vector-equation-of-the-straight-line
- https://brilliant.org/wiki/3d-coordinate-geometry-equation-of-a-line/
- Analytical geometry and linear algebra .2013. D. Mart L. Sabanna
- Vectors in space, vector product, analytic geometry.2016. W. Plawst. T .Constantinno
very good post. friend.