We understand permutation an ordered sequence, built by available elements. The number of permutations of n elements It is given by n factorial that is just calculate the factorial of the number of elements from the set. For a better understanding we will consider the DOG word anagram. Recalling that anagram of a word corresponds to the permutation of letters in a word, forming or not another word. Watch:

In the case of the word DOG, there is no repetition of letters, then we can determine the anagrams using the following mathematical expression: Pn = n!
P3 = 3! = 3*2*1 = 6
The word Dog has 6 anagrams.
Permutation involving a repeated element
Determine the anagrams of the word Puzzles.
The anagrams are formed from a sequence of letters 7, two of which are equal to Z.
This way we have:
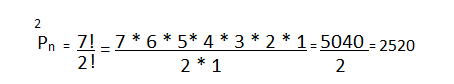
Permutation involving two different elements repeated
Determine the anagrams of the word Quizzing.
Anagrams will be formed from the following eight letters, two of which are equal to I and two equal to Z.
We have:

Other situations involving repeated elements
Anagrams of the word Crackbacks.
In this case we have 10 letters, where the following repetitions occur: two letters A, three letters C and two letters K.
Then:
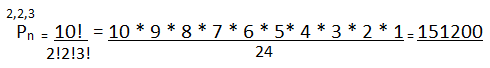
Congratulations @elianoraa! You have received a personal award!
Click on the badge to view your own Board of Honor on SteemitBoard.
For more information about this award, click here
Congratulations @elianoraa! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!