Combinatorial analysis is one of the topics that mathematics is divided, responsible for the study criteria for representing the amount of possibilities to pass a group without having to develop them.
See an example of a combinatorial optimization problem and how to set up their groups.
Given the B set of digits B = {1,2,3,4}. How much natural numbers of 3 digits that can form using the elements of group B?
This is a type of combinatorics problem because we have to form groups, in this case form numbers of 3 digits, ie, form groups with B set of elements taken from 3 in 3.
See how would solve this problem without the use of criteria or formulas that the study of combinatorial analysis can provide.
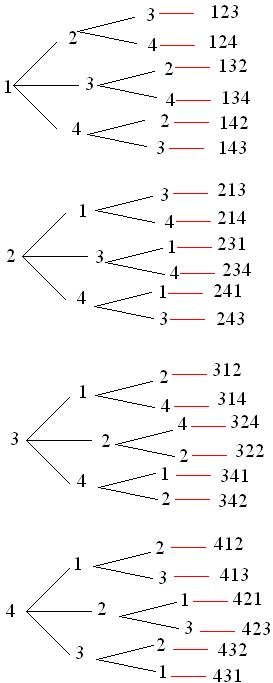
This scheme is built up all natural numbers of 3 digits that can form with the numbers 1,2,3,4, thus concluding that it is possible to form 24 clusters.
To find this amount of possible groupings is not necessary to mount this whole scheme, simply use the combinatorics of study that divides the groups in simple arrangements, simple combinations, simple permutations and permutations with repeated elements. Each of these divisions has a formula and a different way of identification, which we will study in this section.
The study of combinatorial analysis is divided into:
fundamental principle score
This scheme is built up all natural numbers of 3 digits that can form with the numbers 1,2,3,4, thus concluding that it is possible to form 24 clusters.
To find this amount of possible groupings is not necessary to mount this whole scheme, simply use the combinatorics of study that divides the groups in simple arrangements, simple combinations, simple permutations and permutations with repeated elements. Each of these divisions has a formula and a different way of identification, which we will study in this section.
The study of combinatorial analysis is divided into:
fundamental principle, score
Factorial
Simple arrangements
Simple permutation
Simple combination
Permutation with repeated elements.
In another post I will talk more about Combinatorial analysis!