Have you ever wondered why your balance is gradually decreasing or growing during gambling? (roulette, trading, lotteries, bookmaker, poker, etc.). If not, then this series of articles will explain to you the maths behind various gambling activities.
But first the basics. Let's start with a coin toss. The chance of ejecting an head or tails is the same and is equal to 50% (0.5). Of course, this does not mean that the head and tails will come in alternately, the real world does not work that, you can often see the results like (H, H, H, T, H, H, H, T, H ) of which it would appear that the chance of ejecting an head is 70% and tails 30%, but is it true? NO! That's why we've done too few attempts. The coin throwing probability tells us that throwing out an head or tails will be 50% if you throw a coin indefinitely! Below is a graph showing the dependence of the likelihood of head ejection and the amount of coin flips
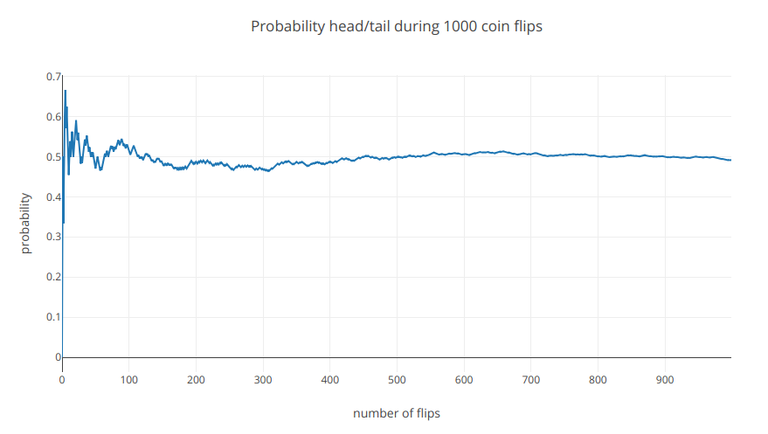
As you can see, the more flips, the more probability is closer to 0.5, is it amazing?!
Well, until now it was easy, now it will be a bit harder. If we are to refer to gambling, the same throwing the dice is not gambling yet. Only when we start betting on someone for the money that results, then we can talk about gambling. So let's begin!
A simple example. I am offering you such a bet, if I fall the head I lose and I pay you 2$, if the tails are the one I win and you pay me 1$. Do you agree to such a bet? Intuitively you will definitely agree, because if the chance is 50/50, so statistically you lose (-1 $) and once you win (+ 2 $), you can guess that with a large number of bets you will nice profit. Well, it's just intuition, and what's the math in it?
At this point, we are dealing with the expected value. The expected value is the value of the winnings you should expect with the number of repetitions striving for infinity! The formula looks like this
EV = pw * vw + pl * vl
where pw is the probability of winning, vw is the value we win, pl is the probability of losing, and vl is the value that we will lose.
Taking our bet as an example
EV = 0.5 * 2$ + 0.5 * -1$ = 1 $ - 0.5$ = 0.5 $
So on average every throw, you win $ 0.5. Of course you will never win that amount in single bet, because your eventual win is always $ 1, but this value tells us how much you win on average for each bet if we bet on endlessly. The chart of your funds after such 1000 bets looks like this
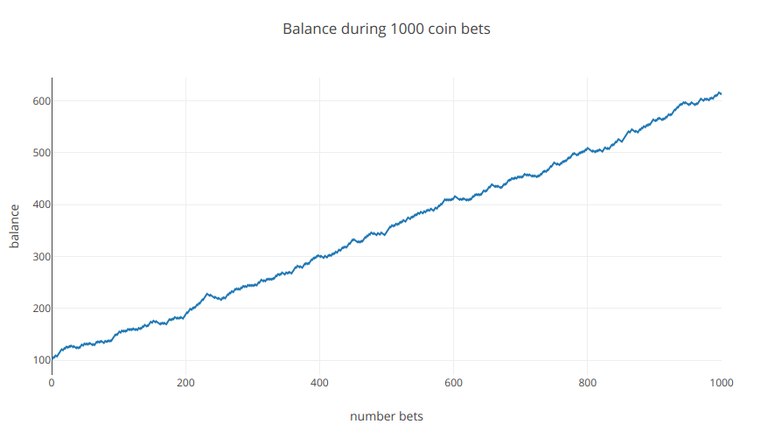
It looks super is not it? Unfortunately, you'll probably never be in this situation :)
Now a bit more complicated example, we will throw a dice. I offer you such a bet, if there are at least 5 dots (5, 6) you win and you get 5$ if you throw less than 5 dots (1, 2, 3, 4) you lose and pay me 3 $. Do you agree to such a bet? Now it is not so easy to make decisions without calculations right? :)
Well, we start from the beginning, the chance of throwing out at least 5 dots (5, 6) is 2/6 (~66%), and less than 5 dots (1, 2, 3, 4) is 4/6 (~33%). So by substituting the data for the formula we get
EV = 2/6 * 5$ + 4/6 * -3$ = 10/6 $ - 12/6 $ = -2 / 6 $ ~ -0.33 $
As you can see, on average on every such bet you will lose about 0.33 $ that is, that betting would zero your funds at some point if we were betting on endlessly. Also below I attach a graph that shows the state of your funds after 1000 plants, as you see in some point you bakrupt.
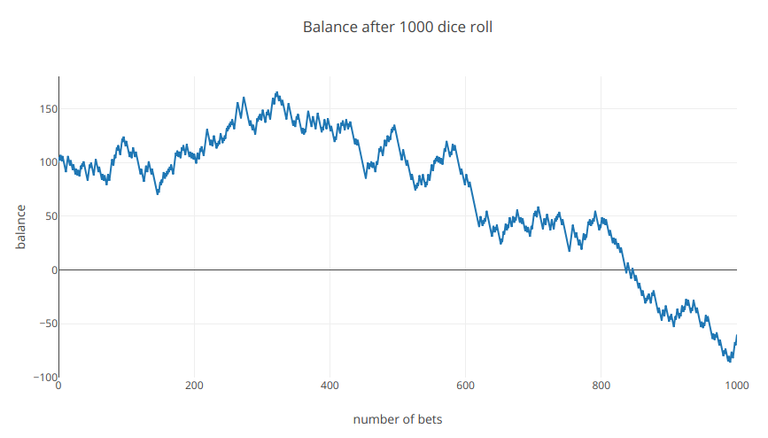
What's more, even for a moment even our funds grew, then to collapse down to 0. This is the so-called phenomenon of variance, which causes some deviations from the average. I will also mention this phenomenon during subsequent articles.
Great, if you read this, it means that you have reached the end and are wealthier with knowledge that will allow you to increase your funds as in the diagram of your state of funds in the coin flip, if you only find situations such as a similar opportunity to bet.
If there is interest in this topic, I will try to insert another article much faster than I intended, greetings!
Congratulations @wojtasss! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Do not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!