Solution to Difficult Problem

A couple of weeks ago I was fed up with all the simple math problems being posed on this site and decided to propose a more difficult one expected of college students. No surprise, no one was up to the task. (Even though as we'll see at the end, this problem was pretty easy.)

I then offered a hint which simplified the problem without actually changing it, but of course, the internet is full of whiny quitters and again, no one was successful, simply because I told them it was too hard for them.

So, as promised, here is the solution to the altered problem stated in the hint above.

Assume a >= b >= 1, we want to show

(Equation 1)

First, consider when a is much bigger than b. it should be clear that the middle term a/(b+1) will be greater than 3/2 all on its own. Let's make this more precise and find out when this happens:

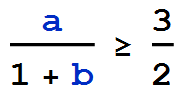Whenever,

Next, going back to Equation 1, it should be clear the 3rd term 1/(a+b) will contribute the least of the 3 terms, so let's find out when the first two terms satisfy the inequality. That is, when is this true?

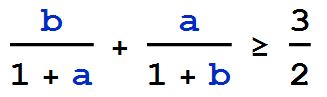
We're going to make our first approximation. Note that because we are assuming a >= b, if we substitute a for b in the denominator of the second term, we make the sum smaller, that is

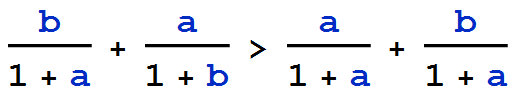
So if we make the right hand side greater than 3/2, the left hand side will also be greater than 3/2. Thus we consider

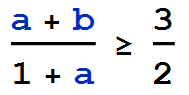Skipping the algebra we get,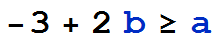

So what have we shown? We've shown that whenever, holds, the second term in Equation 1 satisifies the inequality and when, 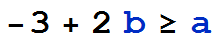holds, the first two terms are enough to satisfy the inequality. Thus the inequality can only fail if both of these inequalities fail, that is when

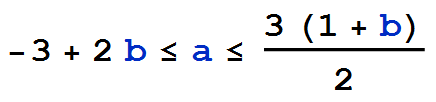
Thus, we have proven what we want to prove, except when a and b satisfies the above double inequality. But what does that mean? The biggest problem students have with algebra, is their inability to visualize what's going on. And for some strange reason, it never occurs to them to graph what is going on. Most likely, because when they learned to graph a function, they didn't learn what the picture means. So let's graph the above inequalities to see what's going on. In the plot below, b-values are represented along the horizontal axis and a-values along the vertical axis.

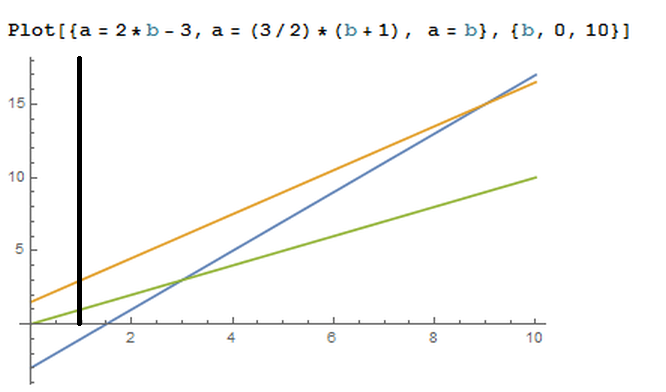
The black line, I added after Mathematica did the plotting for me. This occurs when b > 1, which is one of our first assumptions.
The green line, is when a=b, and since we're assuming a >= b, we're considering everything above the green line.
The blue line is a = 2b-3. Since we know everything below the line satisfies the original equation, we want those values above the blue line.
And finally, the orange line is a = (3/2)(b+1). We know everything above this line satisfies the original equation, so we're left to consider the values that lie below.

To summarize once again, but using this picture. If we note that any pair of values (a,b), we have shown all pairs satisfy the original equation and result in a value greater than 3/2, EXCEPT those pairs lying inside the region trapped by these four lines. Which is a bit surprising considering we started with every possible point in the first quadrant.

As an aside, note that if we solve:

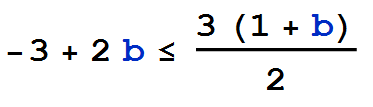we get 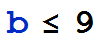, which confirms what our plot above shows, namely, the point (9,15) is the (a,b) pair where the blue and orange lines meet.

If we really wanted to torture ourselves with some algebra, we could take the knowledge we created above and go back to the beginning and use it to cut off another section of this domain. I did this and was quickly able to show b < 3.75, but in the end it doesn't prevent us from needing a bit of calculus. If we take one last look at the plot above, we see the point (1,1) is still in the domain which we have yet to show satisfies Equation 1. Of course, as mentioned in the hint, the point (1,1) is where the value 3/2 is actually attained. And because this value is achieved, no amount of estimating will eliminate every point, which is why calculus is needed to finish off this problem.

I'll let Mathematica do the heavy lifting, so we can get this done quick. Let's consider the derivative of the left hand side of equation 1, with respect to a. Call it

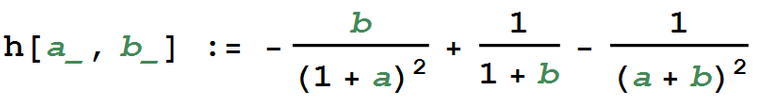
In this context, a is the variable and b is fixed. We've also shown that a can't be too much larger than b, so let's assume a = b + e, for an e small enough to keep us in the domain we have prescribed above. We let Mathematica compute h(b+e,b) for us.

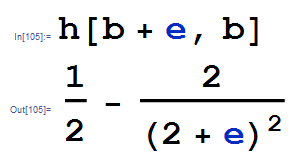
Observe that if a = b, we have e = 0, and so h(b+0,b) = 0. We know when a derivative equals zero, we're at a max or a min. But since e >= 0, we can see for small e>0 that h>0, which means the function is increasing which means when a=b we're at a minimum. Hence for any fixed b as a increases, the original function increases. Because of the symmetry of the problem we can also conclude that for any fixed a, the original function increases as b increases. Thus we're done, because as we move up or toward the right of the point (1,1), the original function increases.

The astute among you will note that the calculus argument holds without all the initial algebra, since we only assumed a >= b. While true, what exactly would you have learned about the problem, if we had skipped straight to the punchline? Then again, I doubt more than one or two made it that far. ;)