Hello friends starting a new stage of publication, today I want to share with all of my knowledge acquired in my professional studies, that is why today I start with the mathematical sciences, where I will discuss topics of great importance which will be published through the title of Mathematical Explanations , since through this theme I will be able to answer many of your doubts of interest, in these publications you will be able to observe a quality content supported by graphical and numerical examples, then I will show my first publication referring to the Classification of Discontinuities, this topic is based on graphical representations and example that shows how the numerical functions have a relation with the behavior of the numerical constants, sample of this relations is the value that exists between the interpretation and the results obtained, I invite you to see this article.
Classification of discontinuities
Continuous functions are very important in mathematics and in different applications. However, not all functions are continuous. It may happen that a function is not continuous throughout its definition domain. If a function is not continuous at a point, it is said that the function has a discontinuity at that point and that the function is discontinuous. In this article we describe the classification of discontinuities for the simplest case of functions of a single real variable.
Previous concepts
Consider a function y = f (x), of real variable x, defined for every value of x except possibly for a certain value x = a. That is, f (x) is defined for x a. Let's also define:
Trend of a function
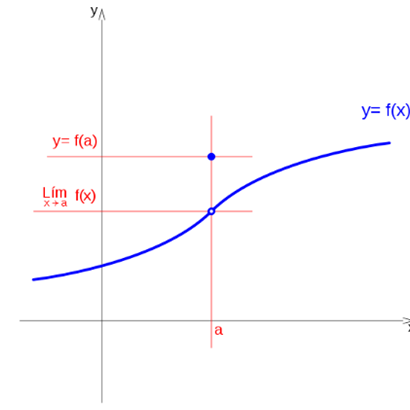
Consider the concept of trend of the function: f (x), in the proximity of a point: a, before using the concept of limit, more formal.
It is said that a function f (x) tends to a value c, when x tends to a to the left, if as x takes values closer to a, without ever becoming a, and lower than a, the value of the function f (x) progressively approaches ac, where c is a real number, then we say that the function converges on the left at c, or that the function is convergent on the left.
If when x approaches aa, without reaching the value of a, and with values lower than a, it takes increasing values, without being able to determine a real value that the value of the function can not overcome, it is said that the function tends to infinity when x tends to the left, in the same way if when x progressively approaches aa, without becoming ay with values lower than a, the value of the function takes lower values each time, without being able to determine a minimum real number that the function can not overcome, it is said that the function tends to minus infinity, when the variable tends to a to the left. In these two cases it is said that the function diverges when x tends to a from the left.
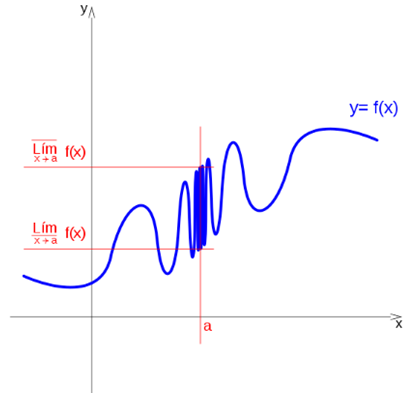
If when the variable x takes values progressively closer to a, but different from a and lower than a, the function oscillates between a higher value Ls and a lower value Li, where Ls is the smallest real value that the function can not exceed when x tends to a on the left, and Li is the highest value for which the function remains above when x tends to the left, the function is said to oscillate between the values Ls and Li when x tends to a to the left, and so both the function, in this case has no limit.
If for values of x close to a, less than a, does not exist because it is not defined or because no real number exists as a result of f (x), it is said that f (x) does not exist to the left of a.

By the same reasoning we can determine the tendency of the function f (x), when x tends to a, without becoming a and with values greater than a, saying that x tends to a from the right, with the same results as those obtained by the left.

Limit of a function
The limit by left in a, that is, the limit when approaching the value x = a by values less than a, such as:
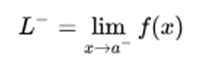
The limit by right in a, that is, the limit when approaching the value x = a by values greater than a, such as:
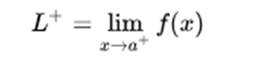
If these two limits in the environment of point a exist and are equal, it is said that the function has a limit at this point.
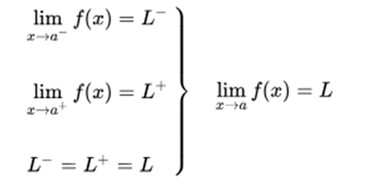
In any other case it is said that the function has no limit at that point.
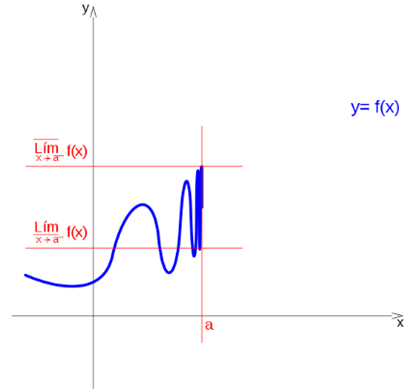
Upper limit and lower limit
Even though a function exists but has no limit at one point, we can differentiate an upper and lower limit.
It is said that a function has an upper limit on the left, at a point a, if there is a higher quota: Ls, that the limit does not exceed when approaching a on the left:
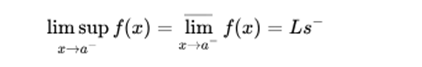
In the same way it is said that a function has a lower limit on the left, at a point a, if there is a lower quota: Li, below which the limit can not be when approaching a on the left:
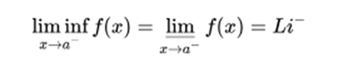
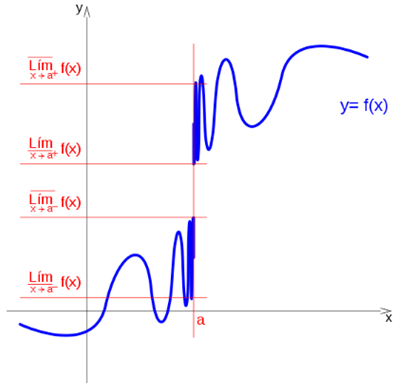
It is said that a function has an upper limit on the right, at a point a, if there is a higher quota: Ls, that the limit does not exceed when approaching a on the right:
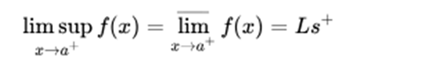
It is also said that a function has a lower limit on the right, at a point a, if there is a lower quota: Li, below which the limit can not be when approaching a on the right:
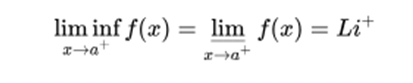
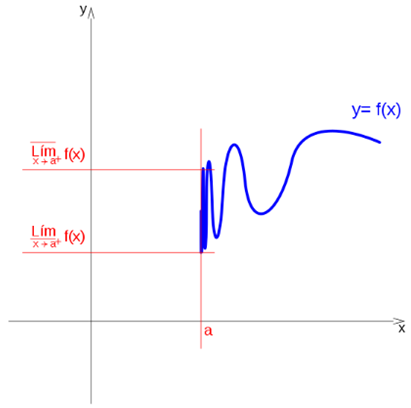
If the upper limit on the right and on the left coincide, it is simply mentioned as the upper limit, in the same way, if the lower limit on the right and on the left coincide, it is mentioned as the lower limit.
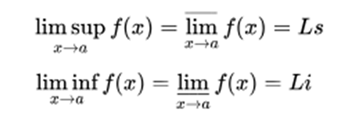
But this coincidence does not have to occur in all cases.
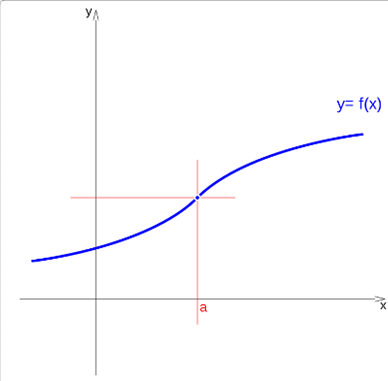
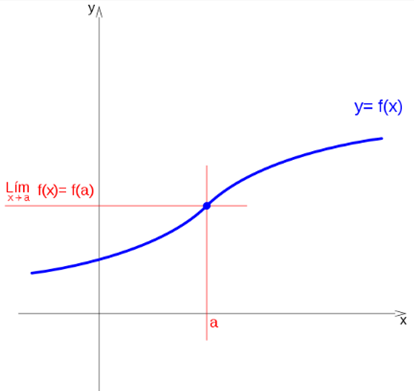
Continuous function
If a function has a limit on a point and its value matches the value of the function at that point, then the function is continuous at that point:
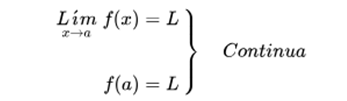
in any other case it is discontinuous at that point.
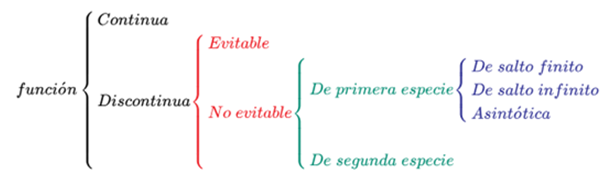
Types of discontinuities
The discontinuity of a function at a point can be classified into:
Avoidable discontinuity
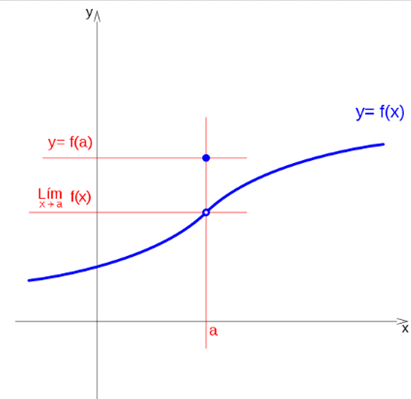
A function presents avoidable discontinuity at a point a, if the limit exists at the point, but the function at that point, f (a), has a different value or does not exist, let's look at these two cases.
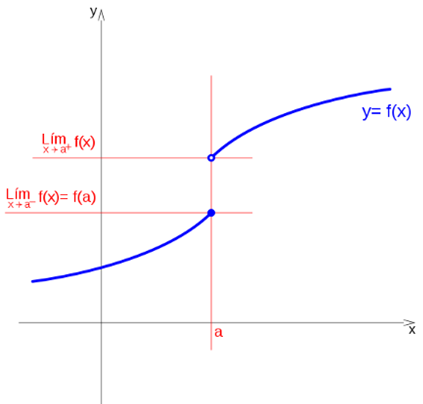
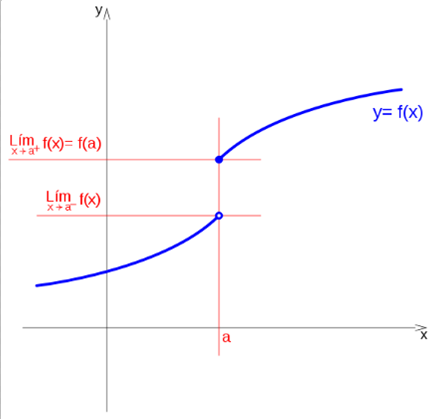
If the limit when x tends to a, is c, and the value of the function evaluated in a is d, the function is discontinuous in a.
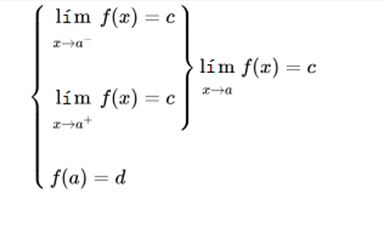
If the function has a limit when it tends to a, but does not exist at that point, the function is discontinuous in a.
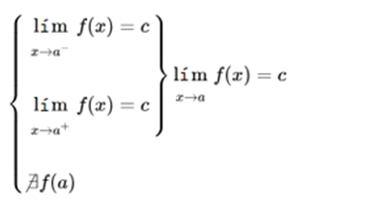
Knowing that a function is continuous at a point, when it has a limit at that point, and the value of the limit is the same as the value of the function at that point, the two previous discontinuities can be avoided by assigning the function, at the point of discontinuity, the value of the limit at that point.
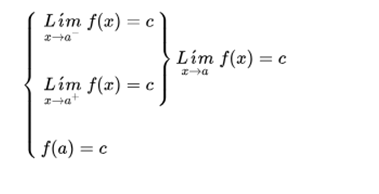
Essential or non-avoidable discontinuity
It is said that a function presents an essential discontinuity when some of the following situations occur:
Discontinuity of first species: if the lateral limits are different, or at least one of them diverges.
Second species discontinuity: if the function, at least on one side of the point, does not exist or has no limit.
Discontinuity of first species
In this type of discontinuity there are three types:
Finite jump
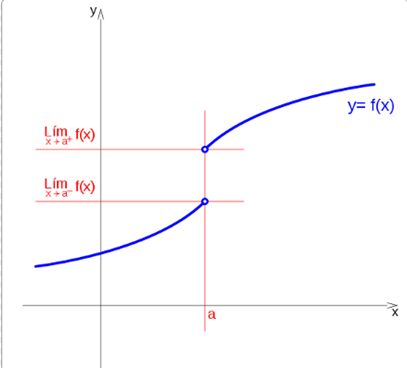
There is a limit on the right and on the left of the point, its value is finite, but they are not the same:
This type of discontinuity of first species is called finite jump, and the jump is given by:
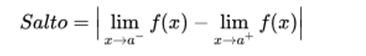
If the function tends to c, when x tends to a to the left, and tends to d when it does to the right, at the point x = a, a jump occurs, regardless of the value of the function at that point.
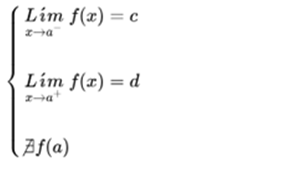
So we can see that they are discontinuities of finite leap:
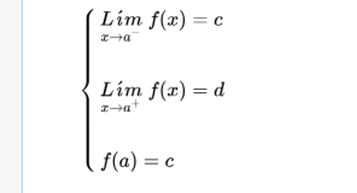
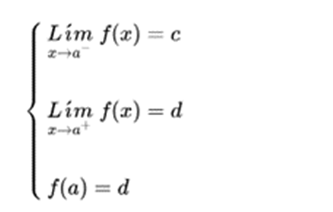
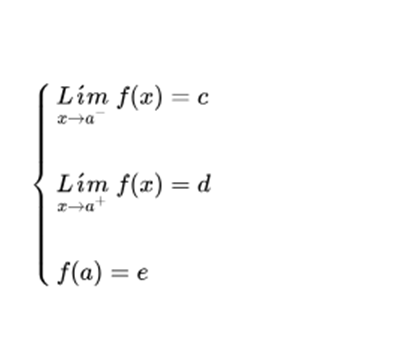
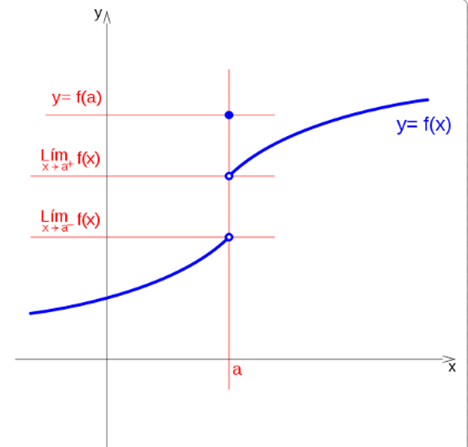
Below is an explanatory video with examples of the various types of Discontinuities:
Bibliography :
- https://en.wikipedia.org/wiki/Classification_of_discontinuities
- http://www.mathwarehouse.com/calculus/continuity/how-to-classify-discontinuities.php
- https://mathcs.org/analysis/reals/cont/defs/disclass.html
- https://math.stackexchange.com/questions/467236/classification-of-discontinuities
- Mathematics Explanation of the properties. 2011, Ricard CHASTER, Marc WSARTER
- Mathematical Discontinuities, representative graphs.2014. Mariana D, Carlos Rodriguez
@minnowbooster this is very good content, especially very educational