
I’ll Order the Blowfish, Please…

Mmmmmmm...deadly blowfish
To no one's surprise, Homer ate the blowfish and now is at risk of carring the deadly 'blowfish' disease. There is a test that is 99% accurate for testing for the 'blowfish' disease.
Meaning:
• 99% of people who test positive are positive
• 99% of people who test negative are negative
The level of the disease in the population is 0.0001 (1 / 10,000)
After 1 million people are tested, Homer’s test comes back positive. How worried should Homer be?

Welp, Homer did test positive…
...and it is 99% accurate...

...and he should be...
not worried at all!

HOMER WILL LIVE!
But wait…how? Isn't the test 99% accurate?
If we were to ask for a quick initial response, I’d suspect most people are going to say,
“Homer should be extremely worried. A 99% accurate test means when you test positive, it’s 99% likely you have the disease.”
But I wouldn’t expect that response from medical practitioners, who’s advice have life altering implications when communicating with patients. Or would I.....? (stay tuned and keep reading).
If you are one to think Homer has a 99% chance of dying from the 'blowfish' disease, I think that is absolutely within reason to think that. I mean after all, most people aren’t paid to interpret results, percentages, and probabilities that have life altering implications. While statistics and math are probably not the first things that come to mind when we think of our medical practitioners expertise, I will argue that statistics should be considered of equal importance to the profession as biology, chemistry, or human anatomy.
Statistics, love it or hate it, can be…well…complex and confusing. Believe me, I’ve been there…and I’m the one with the math degree! And it’s nothing to be ashamed of to admit that it’s tough. I think one of the most challenging parts of working a math problem out is just keeping track of the logical thought processes, patterns, and relevant information. I think that’s why we all dreaded those word problems in school. It was if we were being asked to solve the answer to life, the universe, and everything (which by the way, I finally learned why Siri says “42” when you ask her. If you’ve never read The Hitchhiker’s Guide to the Galaxy, I strongly recommend it.) But If I’m trying to calculate what’s the probably of having a disease that is the 0.0001 of the 99% of a positive or negative test results…my first thought is

followed by…

Thanks Avril...
My issue is I am a visual learner and thought processor. On an exam I was never really concerned that I couldn’t work it out, it was whether I’d run out of time to process it. I need to write it out, draw it out, map it out…whatever you want to call it…I need to organize my thoughts on paper first and to work it through. Sure it’s not the quickest way to solve a problem…but do you want quick? Or do you want correct?

So before Homer starts checking things off his bucket list, that he may or may not regret after his final 24 hours, let’s figure this out.
We are going to solve this using Bayes theorem by saying:
What’s the probability Homer has the disease and tests positive, if Homer tests positive. Which in that case, we’d set up a formula.
*I’m going to do my best to show the logic of where the numbers come from and where they go. Even for me, I really had to sit down and think out the whole mathematical process as I kept getting different answers. Like I said though, I just need the time to work it all out.
Solve with Bayes
This is Bayes Theorem: 
To put it into our context, I’ll change the variables to what we’re actually looking for:
-What's the probability that you have the disease, if you test positive?
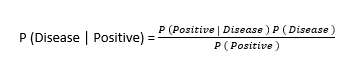
So let’s break down each probability here. There are 3 probabilities (actually the 3rd has 2 ‘hidden’…so technically 4 probabilities we will see)
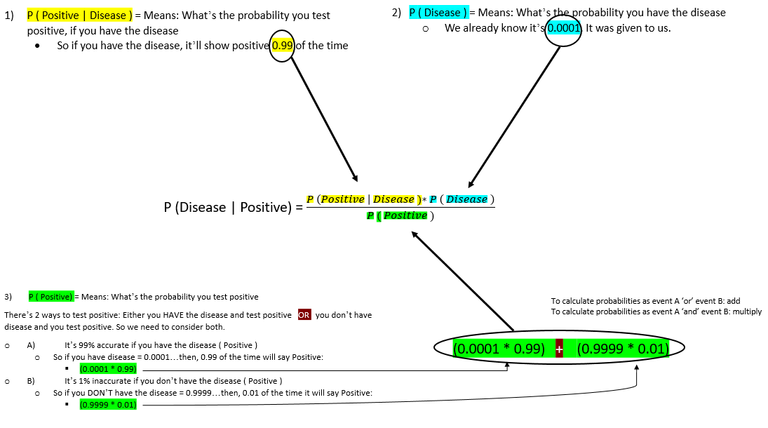
So, the probability of having the disease if you test positive:

It’s no wonder even the brightest of individuals could get lost in the calculations. It’s really hard to make sense of what’s happening when you are trying to calculate percentages of percentages, divided by a percentage of a percentage plus another percentage of a percentage…

Say what????
Like I said, I’m a visual learner. So lets work through it a little differently by putting in values to represent the number of people and break it down that way.
Solve with Visualizing
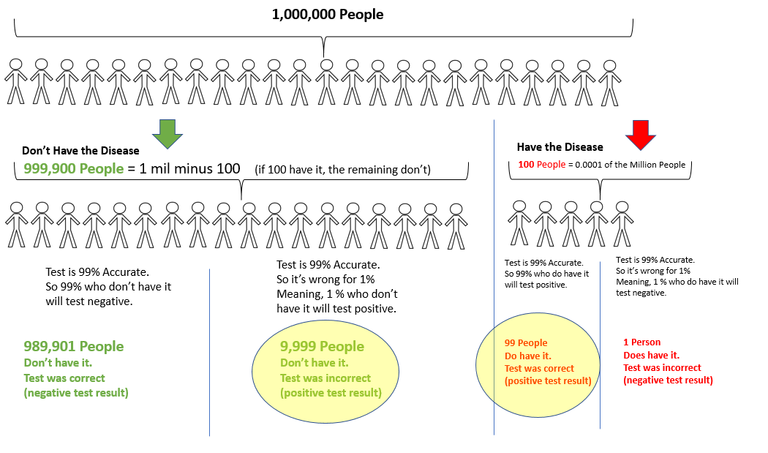
So all we know is that Homer tested positive. Looking at my diagram, we can see two groups tested positive (9,999 who don’t have the disease, and 99 who do). So the question we are REALLY answering is what’s the likelihood Homer is in that small group of 99 who tested positive and have the disease out of ALL the people who tested positive. We calculate that out (99 / 99 + 9,999) = (1 / 102) = and we get the same answer as above, 0.0098…not very likelihood.
But wasn't that easier to understand?
So what's the problem??
A lot of people rely on others to do the math for them. Or quite simply, some people don’t bother to really learn or understand it. Math, like most things in life, is a skill. Sometimes people have that ability to “just get it”. And that’s great! And some people need to really invest a lot of time to learn it. And that’s fine too. But no matter your level or ability, it’s a ‘use it or lose it skill'…and contrary to belief, just because you are smart enough to be a Doctor, doesn’t mean you are naturally gifted intellectually in other areas such as mathematics as well.
It’s like the false belief that just because you are great at basketball or baseball…then well, soccer or tennis will be just as easy, because you’re an athlete!
This post was inspired by an article brought up in my data science class found here:
"Are doctors confused by statistics? A new book by one prominent statistician says they are - and that this makes it hard for patients to make informed decisions about treatment."
Gerd Gigerenzer, a statistician, has seen the scenario I describe above often. Gigerenzer regularly gives statistics workshops, and in 2006 and 2007, started every session to more than 1,000 practising gynaecologists, the same question:
A 50-year-old woman, no symptoms, participates in routine mammography screening. She tests positive, is alarmed, and wants to know from you whether she has breast cancer for certain or what the chances are. Apart from the screening results, you know nothing else about this woman. How many women who test positive actually have breast cancer? What is the best answer?
nine in 10
eight in 10
one in 10
one in 100
That's tough to answer without knowing more. Now, if Gigerenzer follows it with data about Western women of this age to help them answer this question. (* Figures bellow are based on US studies from the 1990s, rounded up or down for simplicity).
- The probability that a woman has breast cancer is 1% ("prevalence")
- If a woman has breast cancer, the probability that she tests positive is 90% ("sensitivity")
- If a woman does not have breast cancer, the probability that she nevertheless tests positive is 9% ("false alarm rate")
In one of his sessions, almost half the group of 160 gynaecologists responded that the woman's chance of having cancer was nine in 10 (90% chance). Only 21% said that the figure was one in 10 - which is the correct answer. That's worse than if the doctors had been answering at random.
The problem is that the doctors are equating "If a woman has breast cancer, the probability that she tests positive is 90%" as "the probability she has breast cancer". Gigerenzer suggests a solution that instead of setting probabilities out as percentages, although standard practice, he is pushing for risks to be expressed using numbers of people instead, and if possible diagrams. I tried my best to display this in my 2 solutions above to find Homer's probability of having the 'blowfish' disease.
Now I don’t pretend to be a doctor, as I’m quite a few credits short of my medical degree 😉. Nor do I feel my recommendations to people based on some symptoms I put into WebMD makes me more qualified to give anyone a prognosis versus someone who’s earned the title of M.D.
Doctors are highly qualified, and intellectual people. Society as a whole treats their credentials in that way, as well as they should (now if only teachers and educators were also treated as highly qualified in their profession to guide educational standards and policies…but that’s a whole other issue).
I’m not trying to make this post to bash doctors. I believe majority of doctors are not intentionally giving false information…but it does raise a concern that I see very often, not just in the medical field, and that is if you’re going to be supplying information, statistics, ‘facts’ to people, isn’t it your duty to make sure it is correct and accurate? And if your job requires you to understand and interpret probabilities and to understand the impact of recommending a patient to receive or not receive a treatment, shouldn’t doctors know not only the reasons for it or against it, but the real probabilities too?
These doctors can be giving patients information that is life altering! Imagine you are told you have a 99% chance of having a terminal disease that causes death within months based on a test that is 99% accurate, when you actually only have 0.1% chance of having it. Now you tell me how your life decisions would not have changed given that circumstance and information.
I could continue to go on about the other examples Gigerenzer shows about how statistics become misunderstood and used to mis-lead, but I suggest you simply read it...it's quite interesting. Perhaps the most notorious example he refers to when we think of risk as a percentage instead of an actual number/persons, is when the UK's Committee on Safety of Medicines warned doctors that a new oral contraceptive pill doubled the risk of thrombosis.
This lead to 1000s of women, suggested by their doctors, to discontinue the pill. So what’s the issue? The risk had merely increased from a 1 in 7,000 chance of getting the disease to a 2 in 7,000 chance (...yup, it doubled). The following year, there were 13,000 additional abortions in the UK. Certainly more information would be needed to determine if there was a correlation. But regardless, I think you get the point.
The real problem with statistics is that it is very easy to have the maths saying anything you want. Very nice example with the disease (an Homer). First time I see it :)
It really is. You can spin it in any way to your favor. Unless you're paying attention or can actually get the data, you can completely fall into the trap. The example of the risk 'doubling' is a perfect example of that. It makes it sound much more of a concern than it really was...it went from a 0.00014 chance to a 0.00028 chance...it's really an insignificant difference.
This recalls me something. Someone was fighting to reduce a source of uncertainties on a prediction from 10% to 5%. It is nice, in principle, except when the dominant source of uncertainties corresponds to a 50% error.
Lake Titicaca.....Nicaragua! Aqua! For my bunghole....
Sorry?
Well, maybe not :D
Do you have T.P. for my bunghole? I would hate for my bungholio to get polio.
Please try eating 5 fruits a day. It could help!
Wow, I am thrilled to see another math and stats enthusiast posting about Bayes here! You're doing great work, @stats-n-lats, keep it up. :)
Thanks @somethingburger. I'm looking forward to your posts as well.
great
Congratulations @stats-n-lats! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPAlso, your link for image 8 at the bottom does not work.
Ah yes. I'll fix that as soon as I get to my laptop. I usually set it all up and then paste the links in at the end before submitting the post. Just must have missed that one.
Thats what I do too, it's really easy to miss something. :)
I really liked the visual breakdown of the calculations (I'm also a super visual learner). Thanks for the post!
Congratulations @stats-n-lats! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP