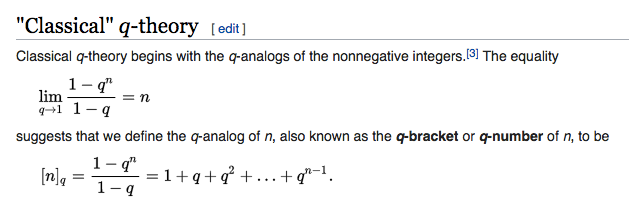Not only that, but yes.
For q in the complex numbers C, the neat thing that e.g. u(18,q) is the number 18, but you can apply analytic operations to it. For example, you can take the derivative d/dq of u(18,q) and you get some other creature.
The q-analog of some binomial coefficients (there are a few) have also hands-on interpretations in the combinatorics of particular spaces, where e.g q index the dimension.
Going further towads what I said at the end, you can use the principle even with a broader approach.
Consider any sort of space Q (such as the complex numbers, but also R^3, if you will) and let p be a point in Q. Let A be some sort of algebra in which division with a unit makes sense (such as the complex numbers). Consider now a sequence of functions Q->A i.e.
a : N -> (Q->A)
This
Define the deformation of a natural number n in N as
[n]_a(q,p) := sum over k from 0 to (n-1) of a_k(q) / a_k(p)
In the limit q to p, the quotients a_k(q) / a_k(p) become 1 and thus
[n]_a(p,p) = n
This is like the above situation, except before a_k(q)=q^k was a very simple function. There is no need to restrict outself to that, execpt that the above sum u(k,q) has a closed expression representation.