[1]

Infinitely many tasks in Finite amount of time?

Today I will post about old but gold philosopical paradoxes; all are considered as supertasks .

0. What is a Supertask?

A supertaks is a task that consists in infinitely many component steps, but which in some sense is completed in a finite amount of time. Supertasks were studied by the pre-Socratics and continue to be objects of interst to moder philosophers. The term "supertask" itself was first used by Jame F.Thomson in 1954. Among many examples of supertasks, I will post about supertasks related to mechanics since we can model as well as analyze these tasks using the concept in physics.

1. Zeno's paradox

[2]

The most famous example is the Zeno's paradox. The runner begins at $x=0$ and runs toward the finish line at $x=1$ .

First he runs $1/2$ of the distance, so that the current position is at $x=1/2$ .
Next he runs half the remaining distance, so that the current position is at $x=\frac{1}{2} + \frac{1}{4}$ .
Again he runs half of the remaining distance, so that the current position is at $x=\frac{1}{2} + \frac{1}{4} + \frac{1}{8}$ .
Formally, let's define the step $T_n\ (n \geq 2)$ to be the task performed by runner running from

$x = \frac{1}{2} + \frac{1}{2^2} +...+ \frac{1}{2^{n-1}}$

$x = \frac{1}{2} + \frac{1}{2^2} +...+ \frac{1}{2^{n-1}} + \frac{1}{2^{n}}$

. He continues in this way infinitely many times, getting closer to the finish line. Now Zeno's question was

Can he ever complete these infinite number of tasks?

Zeno answered this question as NO. We all know that Zeno was wrong, but why did he answered as no?

The question from Zeno, needs to be clarified since the meaning of completion is vague. To solve this paradox, we need to clarify the word complete .

First, "complete" can refer to the execution of a final action (step). This sense of completion does not occur, since for every step in the task (say $T_n$ ) there is another step that happens later, (for example, $T_{n+1}$ ) .
On the other hand, "complete" can refer to carrying out every step in the task, which certainly does occur because of the convergence of geometric series

$\sum_{n=1}^{\infty} \frac{1}{2^n} = \frac{1/2}{1-1/2} = 1$

The two meanings for the word "complete" happen to be equivalent only for finite taks , where most of our intuitions about tasks are developed. But they are not equivalent when it comes to supertasks! Unfortunately, Zeno did not realize the difference between finity and infinity. His misunderstanding of the concept of infinity, lead to paradoxical situation that the runner can not reach the finish line.

To sum up, the runner can carry out every step, but there is no final step. Is this the ultimate answer to all supertask paradoxes? Well, let's look at another example.

2. Thomson's Lamp

In 1954, J.F Thomson came up with an ingenius example of supertask, called Thomson's Lamp.

[3]

Suppowe we are given a lamp.

At time $t=0$ we switch off a lamp.
After 1 minute, at time $t=1$ we switch it on.
After $1/2$ minute more, at time $t=1+1/2 = \frac{3}{2}$ we switch it off again.
After $1/4$ minute more, at time $t = 1 + 1/2 + 1/4 = \frac{7}{4}$ we switch it on again.
Formally, the lamp is off at time interval

$\left[ 1 + \frac{1}{2} + ...+\frac{1}{2^n}, 1 + \frac{1}{2} + ...+\frac{1}{2^{n+1}}\right )$

if $n$ is odd, and on if $n$ is even.

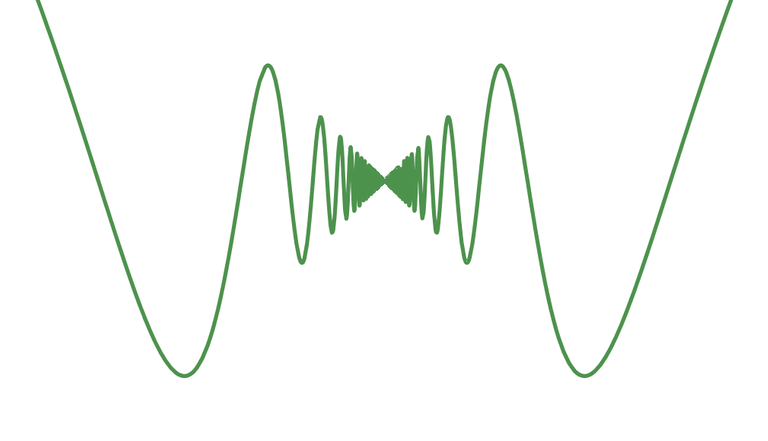
The difference between the Zeno run and Thomson's lamp is that the Zeno run is continuous (the runner's position is continuous on the real line), while state of the lamp is discrete; either on or off. Summing each of the time intervals above gives rise to an infinite geometric series that converges to 2 minutes,

$\sum_{n=0}^{\infty} \frac{1}{2^n} = \frac{1}{1-1/2} = 2$

after which time the entire supertask has been completed. Now the question is

When 2 minutes is up, is the lamp on or off?

If you read section 1, you must realize that the question we asked above is same as asking the final state of the lamp. So using the conclusion of section 1, such state can not exist. Is this true? A lamp that is neither on nor off after 2 minutes...😕

One might argue that such lamp that switches the state infinitely many times can not exist in real world. But this is not a mathematical argument, since switching states infinitely many times is totally valid in theoretical sense.

To solve this paradox, we must clarify the situation. Define a function $f$ such that

$f(t) = \begin{cases}1 & (\text{if lamp is on at time }t)\\ 0 & (\text{if lamp is off at time }t) \end{cases}$

Then, $f(t) = 0$ for all values in interval $[0, 1)$ , $f = 1$ for all values in $[1, 3/2)$ and so on. For convenience, denote the interval

$\left[ 1 + \frac{1}{2} + ...+\frac{1}{2^n}, 1 + \frac{1}{2} + ...+\frac{1}{2^{n+1}}\right )$

as $I_n$ . Now our question is equal to asking $f(2)$ given that the function $f$ is defined on

$[0, 1) \cup \left( \bigcup_{n=1}^{\infty} I_n \right )$

Hmm... is

$2 \in [0, 1) \cup \left( \bigcup_{n=1}^{\infty} I_n \right ) ?$

If does, there should exist an interval $I_n$ such that $2 \in I_n$ . But this is nonsense since

$1+ \frac{1}{2} + ... + \frac{1}{2^{n+1}} < 2$

for all values of $n$ . So, what we are trying to obtain is the function value outside of the domain! Thus, our answer to this question has no right answer .

It can be either on or off after 2 minutes

which is independent of the lamp's switching task on $t \in [0, 2)$ . The description of the Thomson lamp only actually specifies what the lamp is doing at each finite stage before 2 minutes. It says nothing about what happens at 2 minutes, especially given the lack of a converging limit. It may still be possible to “complete” the description of Thomson’s lamp in a way that leads it to be either on after 2 minutes or off after 2 minutes. The price is that the final state will not be reached from the previous states by a convergent sequence.

3. Example of Lamp turned on at t = 2

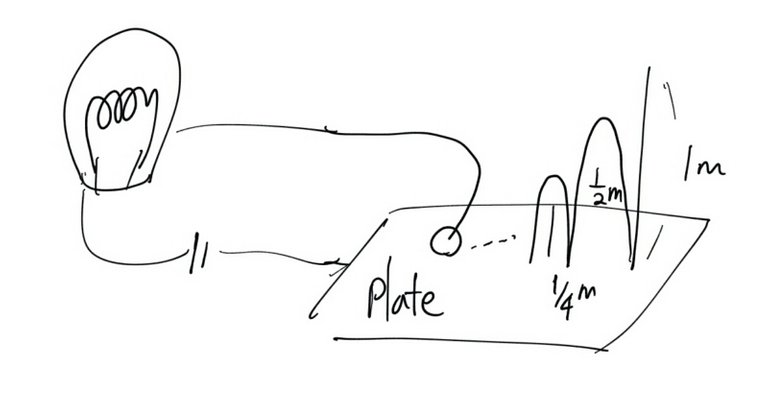
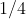
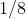
Suppose a metal ball bounces on a conductive plate, bouncing a little lower each time until it comes to a rest on the plate. Suppose the bounces follow the same geometric pattern as before. Namely, the ball is in the air for 1 minute after the first bounce, $1/2$ minute after the second bounce, $1/4$ minute after the third, $1/8$ minute after the fourth, and so on. Then the entire infinite sequence of bounces is a supertask.

Now suppose that the ball completes a circuit when it strikes the metal plate, thereby switching on a lamp. This is a physical system that implements Thomson’s lamp. In particular, the lamp is switched on and off infinitely many times over the course of a finite duration of 2 minutes.

[4]

4. Example of Lamp turned off at t = 2

Alternatively, we could arrange the ball so as to break the circuit when it makes contact with the plate. This gives rise to another implementation of Thomson’s lamp, but one that is off after 2 minutes when the ball comes to its final resting state.

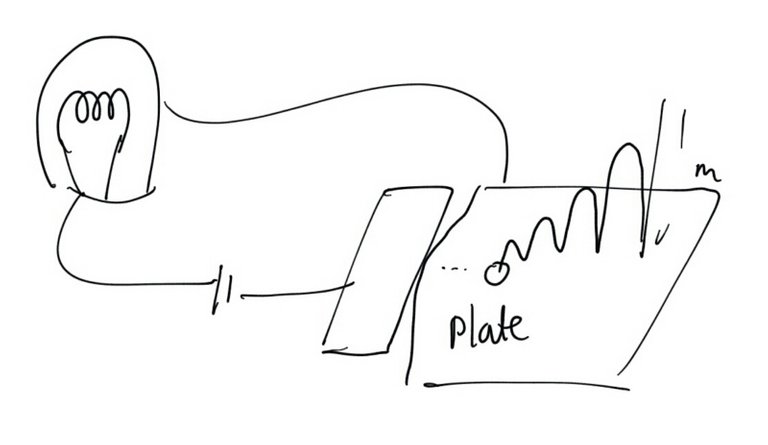
[5]

You can see that if the ball touches the metal plate, current does not flow through the wire passing through the lamp.

5. What is the difference?

The difference between the two supertasks is due to the construction of function $f$ . Since we already constructed a function for Thomson's Lamp, let's do the same for Zeno's paradox.

Define the runner's velocity function as $v(t)$ . It is reasonable to assume that $v$ is continuous over $[0, 1)$ , so that the position function is given by

$f(t) = \int_0^{t} v(x)dx$

on $t \in [0, 1)$ using the fundamental theorem of calculus. Again, fundamental theorem of calculus assures the uniform continuity of $f$ on $[0, 1)$ . Now, this guarantees the existence of left-hand limit

$\lim_{t \rightarrow 1-}f(t)$

which is equal to

$\sum_{n=1}^{\infty} \frac{1}{2^n} = 1$

using the Zeno's paradox. The most surprising fact is that the extension of $f$ by defining

$f(1) = \lim_{x \rightarrow 1-}f(x) = \sum_{n=0}^{\infty} \frac{1}{2^n} = 1$

is indeed unique continuous extension of $f$ ! Therefore, the runner's position after carrying out all the steps should be $x=1$ ; no other choice available.

6. Conclusion

Zeno's paradox can be modeled as a continuous function over half open interval, and this has unique continuous extension which gives unique consequence after completion of all the steps.
However, Thomson's lamp paradox can be modeled as a discontinuous (furthermore, discrete) function over half open interval, and this has multiple extensions (both 0 and 1 are possible outcomes).
Look we started from simple paradox, and ended up with real analysis...😅

7. Citations

[1] Selfmade by GeoGebra 5.0

[2] Image Source Link

[3] Self Made using Drawing App

[4] Self Made using Drawing App

[5] Self Made using Drawing App

Sort:

Trending

[-]

mathowl (66) 6 years ago

I am not sure about the copy right images of those lamps. Could you add the license to it? If your next post has copy right issues steemstem curators might skip it.

$0.00

mathsolver (53) 6 years ago

Sorry I didn't realize that the image was copyrighted. I deleted all images and drew by myself. Next time I'll just draw all the images...

[Math Talk #19] Infinite tasks in finite time? - Supertasks