Rene Descartes
Rene Descartes (1596-1960) is a famous French mathematician and philosopher. He also is a physician, mechanic, physiologist, the founder of modern analytic geometry and algebraic symbolic, the author of the method of radical doubt in philosophy, the author of mechanistic in physics, the creator of forerunner in reflexology. He formulated the following statement in 1637 year – the theory (or the rule) of Descartes.

Image Source
Rene Descartes born in 1956 year in the town Lae. His mother died when he was just one year old. The father of Rene was a judge so he wasn’t in Lae too often. The grandmother of Rene was growing him up. Rene was very unhealthy and curious.
The theorem (the rule) of Descartes
The number of positive roots of polynomial 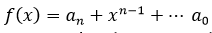 doesn’t exceed the number of signs’ changes in the sequence
doesn’t exceed the number of signs’ changes in the sequence 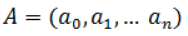 of its coefficients and differs from it by an even number. That’s time to explain the proof of this theorem (rule).
of its coefficients and differs from it by an even number. That’s time to explain the proof of this theorem (rule).
The proof
Let’s assume that 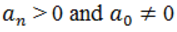 without loss of generality. Let’s hold an induction on the number of sighs’ changes. If in the sequence A there’re not signs’ changes, all non-zero numbers of this sequence are positive, so
without loss of generality. Let’s hold an induction on the number of sighs’ changes. If in the sequence A there’re not signs’ changes, all non-zero numbers of this sequence are positive, so 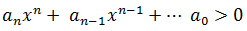 for any
for any  and the polynomial f(x) doesn’t have the positive roots. It’s the base of induction.
and the polynomial f(x) doesn’t have the positive roots. It’s the base of induction.
Let’s suppose now that the theorem is already proved for all polynomials that have a less number of signs’ changes in the sequence of coefficients than q. Let’s suppose that  is a polynomial in which sequence coefficients are equal q changes of signs and c is a positive roof of this polynomial.
is a polynomial in which sequence coefficients are equal q changes of signs and c is a positive roof of this polynomial.
Then:

where’s

i.e.
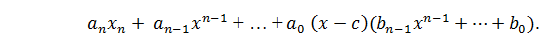
This equation implies that:
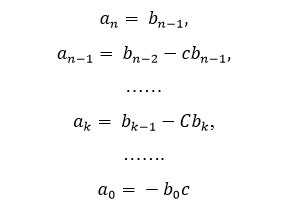
Let’s prove that there’re less signs’ changes  in the sequence B than in the sequence A. Let’s suppose that p – is a number of signs’ changes in sequence B. Let’s notice now that
in the sequence B than in the sequence A. Let’s suppose that p – is a number of signs’ changes in sequence B. Let’s notice now that 
If l is the first place of the signs’ change in sequence B  , the numbers b_0 and b_1 have different signs. If that’s so,
, the numbers b_0 and b_1 have different signs. If that’s so,  what means that the signs of numbers
what means that the signs of numbers 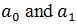 are different. So that, the sequence
are different. So that, the sequence  contents at least one change of sign.
contents at least one change of sign.
Let’s suppose that l and k are two neighboring places of signs’ change in the sequence B. If it’s like that, numbers  have different signs too. Consequently, there’s a change of sign too among the numbers
have different signs too. Consequently, there’s a change of sign too among the numbers 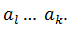
Thank you for attention!
@kental with you!

thanks for sharing this material, I like what you posted. Thank you so much
Thank you! Glad to see your comment.
he was insane!
Of course!
Thanks for sharing!
You're welcome