Polar coordinates

Today we will come back to complex numbers. As discussed before, a complex number z is represented as a + b * i with a and b real numbers and i the imaginary unit (the square root of -1). Since this is uniquely defined by two real numbers, we can think of the complex numbers as a 2D plane, a giving the position in the horizontal direction and b vertical just like any point on a world map is described by its latitude and longitude.

When you think about maps/locations on a smaller scale, you will often make or hear statements like “The train station is two kilometers north of my house” or “Vienna is three hundred kilometers south-east of Prague”. You might realize that if we pick a starting point, we can describe any other point on the map/plane like this, by giving a direction and distance from the starting point. For complex numbers the starting point is 0 (0+0*i) and we can alternatively write any complex number as a pair (r,p) where r is the (positive) distance (r for radius) and p (which is supposed to be the Greek letter phi) is an angle between 0 and 360 degrees (technically, we have to allow the angle to be zero but never 360°; the reason for this will become evident later). This is known as polar coordinates.

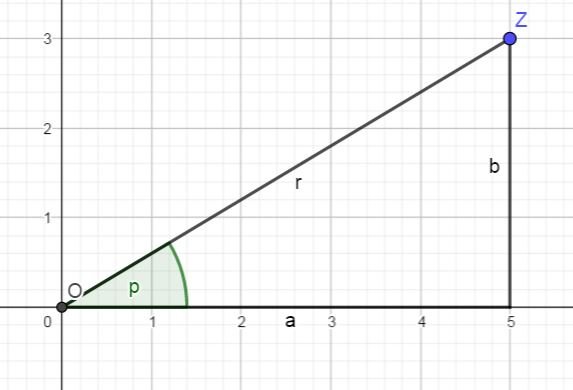
Now we need a way to convert the two notations a + b * i and (r,p) into each other. As you can see in the picture, a, b and r form a triangle with a right angle in the lower right. This allows us to use the sine and cosine function: sin(p) = b/r as well as cos(p) = a/r (this is just the definition). This directly yields a = r * cos(p) and b = r * sin(p).
The other way around, the Pythagorean theorem gives r^2 = a^2 + b^2 and p can be then be calculated using the inverse of the sine or cosine function.

Now what is all this good for? As mentioned in my first post about complex numbers, any equation like z^n = w can be solved there so obviously taking powers of complex numbers is kind of important. Sadly, taking high powers of sums like a + b * i becomes very difficult. This gets way easier in polar coordinates. In fact there is a very general property: if z has polar coordinates (r,p) and w has (s,q) then the polar coordinates of z * w are (r * s,p+q).

Showing this isn't too hard but it takes some work we don't want to do here. You can make some sense of this property when realizing that positive (real) numbers will always have an angle p of zero and negative numbers an angle of 180°. Multiplying two negatives will bring the angle to 360°, essentially the same as zero (since 360° is a full circle, these describe the same direction; the same will apply for any two angles with a difference divisible by 360). Using induction we can extend this property to general products with any number of factors w * x * y * z * … where the new radius will always be the product of the old ones and the new angle the sum of the angles going in, looping back to zero if it exceeds 360°.

Now we are interested in the special case z = w (= x = y = …). For z = (r,p) this means z^n = (r^n,n * p). In particular, this helps us to solve an equation like z^n = w. If we know w has polar coordinates (s,q), finding the polar coordinates (r,p) of z boils down to r^n = s and n * p = q. Both of this can be easily solved (remember that s is positive).
It also becomes evident here that there might be more than one solution. This is well known already for real numbers, e.g. (-2)^2 = 2^2 = 4. Here the reason is that an angle of zero is essentially the same as 360° and could in this case be reached by 2 * 0° (in 2^2) or 2 * 180° (in (-2)^2). As noted before we can argue that p+360° “=” p for any angle p. In fact, there are always n solutions z to z^n = w, one that never reached 360°, one that did so once (and was reset to zero by us), one that did twice, … and finally one that looped around n-1 times. Looping around n or more times is not possible since the initial angle was smaller than 360°.