Several days ago, I made a post about two simple geometry questions. Here I present my solutions:
Question 1:
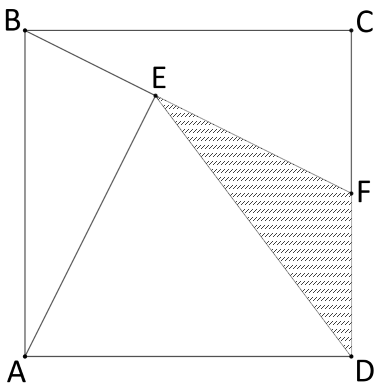
Given that CF = FD and that  , what fraction of square ABCD does
, what fraction of square ABCD does 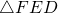 occupy?
occupy?
Solution 1
Place the corners of the square at (0,0), (0,1), (1,1) and (1, 0). The equation of line BF can be given by y = 1-0.5x and the equation of line AE can be given by 2x. Equating these gives x = 0.4 and y = 0.8 The area of triangle FED is therefore 1 - 0.2 - 0.25 - 0.4 = 0.15 or 3/20
Question 2:
Arc IFJ is one-quarter of a circle with center H. Given that HJ = IH = 6, and that EFGH is a rectangle with EH + HG = 8, what is the perimeter of the shaded region?
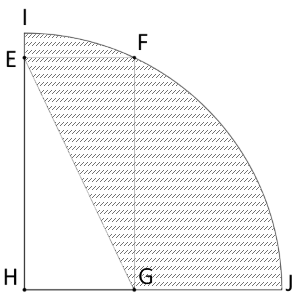
Solution 2
HF is a radius, and also a diagonal of EFGH, so EG = HF = 6. Next EG+HG = 8, but IH+HJ = 12, so the IE+GJ = 4. Finally, Arc IFJ is one-quarter of a full circle or 3π, so the total area is the sum of these segments, namely: 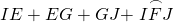 = 10 + 3π.
= 10 + 3π.
Did you edit your original post to include the hypothesis that F is the midpoint of CD in question 1?
Because I recall thinking multiple times that the problem would be much easier if we knew this fact.
I think I edited it 1 or 2 hours after the original post, because I forgot to put it in. Sorry if that threw you off.
That's life! ;)