Operations on Complex Numbers and DeMoivre's Theorem

Stunning fractals can be created using complex numbers. Source: http://users.math.yale.edu

In the previous post, I showed how complex numbers developed, what they mean, and how they can be represented. In this post, we'll talk a bit about operations on complex numbers and go further into how we can find nth roots of complex numbers.

Operations on Complex Numbers

Before talking about binary operations, we'll talk about complex conjugates. The complex conjugate of a z, denoted as 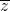number is the complex number that has the same real part, but an imaginary part with the opposite sign. That is to say: 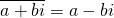. In other words, if you're plotting the complex number as a "vector" in the complex plane, then it is the conjugate of z is obtained by reflecting z over the Real axis.

Source: wikipedia.org CC BY-SA 3.0

For addition, subtraction, and multiplication, you can essentially treat the imaginary unit as if it were a variable.

• Addition: To add any two complex numbers, simply add the real and imaginary parts separately. In other words:
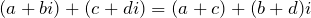
• Subtraction: Similarly, for subtraction, simply subtract the real and imaginary parts separately. In other words:
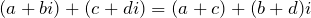
• Multiplication: To multiply, you can use the FOIL method. Once if you see an 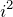, replace it with -1. For example, to multiply 5 + 3i and 2- i, you would write:
  

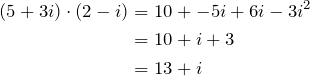
• Division: Division is a bit more tricky. To do this, we write the two complex numbers as a fraction, and then multiply both the top and the bottom by the conjugate of the denominator, thusly:
  

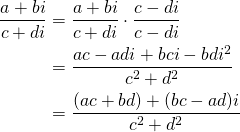
  Multiplication in Polar Form

  
  Recall from the introduction to complex numbers that any complex number a + bi can be expressed as , where r is the modulus and theta is the angle between the complex number and the positive real axis. In fact, if we take r to be equal to 1, the real and complex parts correspond to points along the unit circle. For instance, the point 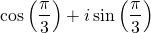corresponds to the rectangular form 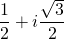, which in turn matches up with the x and y coordinates for θ = π/3 on the unit circle.

  For our next example, it will be helpful to think of the real and imaginary components being x and y coordinates along the unit circle. Consider what happens when you multiply a complex number by another. For any two complex numbers in polar form, I have:

  

  And gathering like terms, I obtain the following:

  

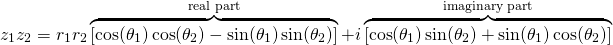
  Hopefully, you've noticed something about the real and imaginary parts. If you remember that these are simply the angle additions for cosine and sine respectively, the equation simplifies to:

  

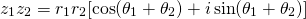
  Essentially, to multiply two complex numbers that are in polar form, you multiply the moduli, and add the angles. Graphically this means that multiplying a complex number by another rotates the original number by the counterclockwise angle of the second angle.

  

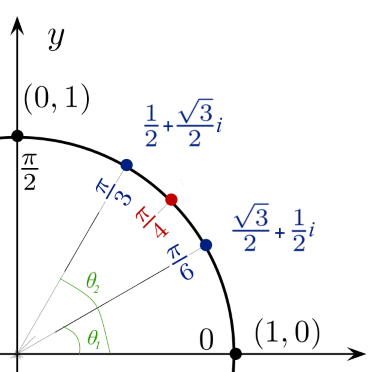
  For instance, to multiply the complex numbers 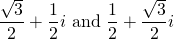, which correspond to π/6 and π/3, respectively, all you need to do is add the angles together, arriving at π/2. The product of the moduli is 1, so: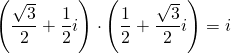

  

  This can also be verified by the FOIL method. This is up to the reader.

  DeMoivre's Theorem

  From the above, it should be obvious that multiplying a complex number by itself n times multiplies the original angle by n and also multiplies the modulus by itself n times. Therefore:

  

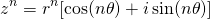
  That's all for today.

  In our next post, I will talk about how to find roots of unity, as well as roots of complex numbers. Be sure to come back for the conclusion to this series.