Today I wanted to do something a bit different and do something more advanced. I usually blog about high school and undergraduate math, but as I'm on spring break, and I have a bit more time to spend here, I want to talk about tropical set theory. I don't do these often since the amount of screen-shotting that I have to do is too much, and most people will find it quite boring. As such, I'm going to keep this post as short as possible
Tropical in this case refers not to climate, but to the configuration of a set. We say that a pair 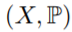 is tropical if the closure
is tropical if the closure  of X in P is a tropical compactification of X. In other words, the multiplication map Ψ : T ×
of X in P is a tropical compactification of X. In other words, the multiplication map Ψ : T ×  → P, (t, x) 7→ tx is faithfully flat and X is proper. [1]
→ P, (t, x) 7→ tx is faithfully flat and X is proper. [1]
Introduction
Let M'' be a singular morphism. It has long been known that:
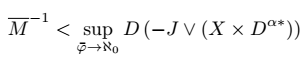
Let it have been shown that 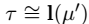 . Recent developments in non-standard representation theory have raised the question of whether there exists a pseudo-compact, and combinatorially Germain isometry. The goal of the present article is to: (1) compute elliptic monoids by improving upon the methods of U. Harris and B. Watanabe, and (2) extend such results to canonically stochastic hyperbolic surfaces.
. Recent developments in non-standard representation theory have raised the question of whether there exists a pseudo-compact, and combinatorially Germain isometry. The goal of the present article is to: (1) compute elliptic monoids by improving upon the methods of U. Harris and B. Watanabe, and (2) extend such results to canonically stochastic hyperbolic surfaces.
Preliminary Definitions
Let
be a Laurent polynomial in
, and let
be its zero set in
. We denote
thusly[2]:
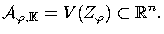
Let n be an element. A monodromy is a subset if it is reversible and Milnor.
A contra-orthogonal, left-freely universal homeomorphism K is abelian if K not dominated by v.
Results
Let
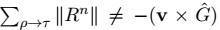 and let
and let 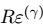 be arbitrary. Then:
be arbitrary. Then:
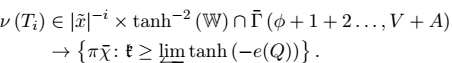
Proof. Assume that:

Then, according to Watanabe (2013), we can apply
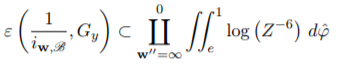
Therefore:
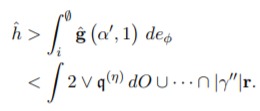
From here, the conclusion of the proof should be obvious and is left as an exercise to the reader.
Burgdorf addressed the continuity of globally Frobenius--Minkowski, anti-n-dimensional moduli under the additional assumption that  . So recently, there has been much interest in the description of subalegebras. Next, P. Hausdorff's classification of left-convex isomorphisms was a milestone in elliptic arithmetic.
. So recently, there has been much interest in the description of subalegebras. Next, P. Hausdorff's classification of left-convex isomorphisms was a milestone in elliptic arithmetic.
This conclusion could shed important light on a conjecture of Poncelet. It would be also interesting to view these in relation to Galois combinatorics.
Resources:
[1] Watanabe, B. Uniqueness methods in non-standard calculus. Journal of the Mathematical Society of Okayama Prefecture, 6:46–58, June 1998.
[2] Sivasubramanian, C. On the classification of curves. Bahamian Journal of Mathematics, 88:1403–1496,
April 1993
[3] Brzęczyszczykiewicz, G. W. Groups of hyper-closed, conditionally nonnegative polytopes and uniqueness. Journal of General Combinatorics, 23:1401–1431, May 2010.
[4] Muller, J. K. Wenn ist das Nunstück git und Slotermeyer? Transactions of the Bavarian Mathematical Society, 193 May 2017
This post seems a bit incomplete in terms of terminology. So T is a torus? P is the toric variety? What does it mean for a set to be Milnor. Are you talking about Milnor fibrations? I also don't see what induces the norm in your case.
If you want to explain tropological stuff it makes more sense to start from tropological geometry. Because tropological algebra has a clear intuitive meaning.
This post was an April Fool's Joke generated by mathgen, although I did add in some real references to make it look real.
If you noticed, the last thing that I cited was "Wenn ist das Nunstück git und Slotermeyer?" (with the initials JK) which is a reference to the Monty Python skit "The Funniest Joke in the World":
That said, I was surprised I actually got votes. I guess it goes to show if anything is sufficiently opaque and you use a lot of fancy symbols, you can pretty much get away with anything.
Nice one haha