Ein zentraler Begriff der Informatik und Mathematik ist die Rekursion. Sie beschreibt das Prinzip, das ein Vorgang sich wiederholt, bis eine Bedingung erfüllt wurde. Das hört sich für den erfahrenen Leser jetzt stark nach einer Schleife an, jedoch existieren bei der Rekursion ein paar Spezialitäten, die in diesem Post anhand eines Beispiels erläutert werden. Viel Spaß!

---

Spieglein Spieglein

Wer sich bisher noch nichts unter dem Begriff Rekursion vorstellen kann, der kann wenn er möchte sich zwischen zwei Spiegel stellen, deren spiegelnde Seiten sich gegenüber stehen. Wenn man sich nun zwischen die Spiegel stellt und in einen der beiden schaut, kann der Eindruck entstehen, das gesehene Spiegelbild sei unendlich weit. Diese unendliche Weite entsteht durch Rekursion. Denn das Spiegelbild des Spiegelbilds ist ein Spiegelbilds des Spiegelbilds :-D

---

Fibonacci

In der Mathematik ist die Fibonacci-Folge ein sehr beliebter Algorithmus (Verdammt klingt dieser Satz langweilig...). Aber im Prinzip ist er ganz simpel: Die ersten zwei Zahlen sind vorgegeben. Sie sind 1 und 1. Nun wird die letzte bekannte Zahl der Folge mit der Vorherigen addiert. Dies ergibt die nächste Zahl der Folge.

1 1 2 3 5 8 13 21 34 55 89 144 ...
Dieses Muster lässt sich an vielen verschiedenen Stellen in der Natur wiederfinden. Im Titelbild war bereits eine Muschel zu sehen. Sie ist ein klassisches Beispiel für die Veranschaulichung des Algorithmus. Im folgendem Bild ist die Folge markiert:

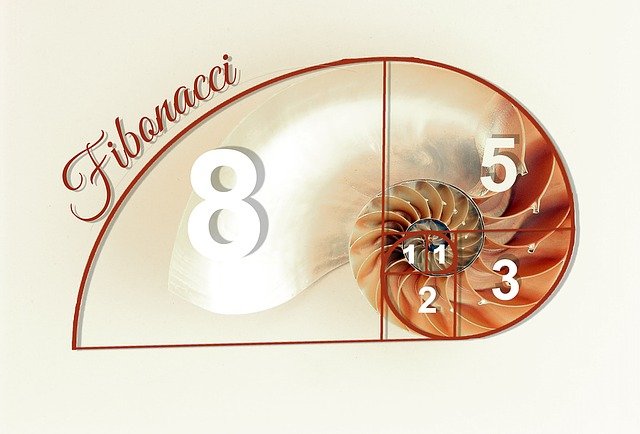
Doch zurück zur Rekursion: Wir haben nun festgestellt, dass das nächste Ergebnis der Fibonacci-Folge aus den beiden vorherigen berechnet wird. In der Informatik lässt sich ein solcher Vorgang mit einer einzigen Methode lösen, die sich selber aufruft, bis eine Bedingung erfüllt wurde. Diese Methode ist rekursiv.

---

Erklärt an einem Beispiel

Als Beispiel für die "technische" Erklärung der Rekursion habe ich mir das Potenzieren ausgesucht. Bei Potenzieren hat man die Basis und den Exponenten.

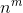
Hier ist n die Basis und m der Exponent.

Schleife

Die Lösung in einer Schleife mit der Basis 3 und dem Exponent 4 würde wie folgt aussehen:

public static void main(String[] args){

   int basis = 3;
   int exponent = 4;
    
   int ergebnis = 1;

   for(int i = 0; i < exponent; i++){
      ergebnis *= basis;
   }

   System.out.println("Das Ergebnis ist: " + ergebnis);

}

Ausgabe: Das Ergebnis ist: 81

Rekursive Methode

Die Lösung der Aufgabe mit einer Schleife war recht einfach. Nun kommen wir zur rekursiven Lösung. Die Basis bleibt bei 3 und der Exponent bei 4.

public static void main(String[] args)
{
    int basis = 3;
    int exponent = 4;    

    System.out.println("Das Ergbnis ist: " + potenzieren(basis, exponent));
}

public static int potenzieren(int basis, int exponent){

    if(exponent > 0){

      return basis * potenzieren(basis, exponent - 1);

    }else{

      return 1;

    }

}

Ausgabe: Das Ergebnis ist: 81

Was ist zu diesem Quellcode zu sagen? Bei einer rekursiven Funktion ist es wichtig, dass es einen Punkt gibt, an dem diese anders greift als zuvor und damit den rekursiven Aufruf stoppt. In diesem Fall wird, wenn der Exponent 0 ist, eine 1 zurückgegeben, statt die Funktion erneut aufzurufen und das Ergebnis mit der Basis zu multiplizieren. Das hängt damit zusammen, dass jede natürliche Basis mit dem Exponenten 0, 1 ergibt.

Für den Fall, dass du eine rekursive Funktion programmieren möchtest, aber das Programm nicht beendet wird, solltest du die Bedingung in der rekursiven Methode überprüfen ;)

---

Ich hoffe dir hat dieser Beitrag gefallen und du konntest etwas daraus mitnehmen. Wie ist deine Meinung zu rekursiven Funktionen oder der Fibonacci-Folge und ihrer Verbundenheit zur Natur? Lass es mich in den Kommentaren wissen :)

Kleiner Hinweis: Man muss keine aufwendige Entwicklungsumgebung aufsetzen, um mal ein wenig mit Quellcode rumzuspielen. Auf der Seite CompileJava.net kann man direkt im Browser Java-Code schreiben, kompilieren und ausführen lassen. Schaut doch mal vorbei ;)


Danke fürs Lesen
CuBy

PS: Fehler bei der Rechtschreibung und Grammatik sind stilistische Mittel und vom Autor bewusst platziert worden. :-D