
Selama ini konsep Faktor Persekutuan Terbesar (FPB) dan Kelipatan Persekutuan Terkecil (KPK) dari dua bilangan masih diajarkan secara prosedural baik itu mencari kelipatan ataupun dengan pemahaman bilangan prima dan faktorisasi prima. Cara seperti ini sering membuat para siswa kesulitan dalam menentukan FPB dan KPK tersebut. Untuk mengatasi hal yang demikian, maka penulis akan menawarkan sebuah solusi dalam pembelajaran matematika materi KPK dan FPB di sekolah dasar diajarkan dengan Pendekatan Matematika Realistic (PMR) model penyajian paket makanan. Pembelajaran matematika dengan pendekatan ini diyakini dapat membuat siswa belajar seakan-akan mereka menemukan sendiri konsep FPB dan KPK yang dipelajari dan akan menjadikan pembelajaran lebih bermakna sehingga pada akhirnya akan meningkatkan pemahaman siswa pada konsep FPB dan KPK.
Sebagaimana kita ketahui bahwa dalam Pendekatan Matematika Realistik (PMR) siswa diajak untuk memahami permasalahan, baru kemudian dari permasalahan siswa diajak untuk sampai kepada bentuk umum dari permasalahan yang sedang dibahas. Dahulu siswa harus dipaksakan untuk menghafal metode-metode yang digunakan para ahli, yang belum tentu sesuai dengan taraf perkembangan siswa. Berbeda halnya dalam pendidikan matematika realistis, siswa diharapkan dapat membangun konsep sesuai dengan taraf perkembangannya (Sembiring dalam Zulkifli, 2007).
Ada 3 prinsip utama yang harus dimunculkan dalam pembelajaran PMR, yaitu:
- Penemuan terbimbing dan matematisasi progresif yaitu melalui topik-topik yang disajikan, siswa harus diberi kesempatan untuk mengalami proses dan menemukan kembali ide-ide dan konsep-konsep matematika. Hal ini dilakukan dengan memberikan masalah nyata yang mempunyai berbagai kemungkinan solusi, dilanjutkan dengan Mathematizing prosedur solusi yang sama serta perancangan rute belajar sedemikian rupa, sehingga siswa menemukan sendiri konsep-konsep.
- Fenomenologi didaktis yaitu menekankan pentingnya masalah konstektual, untuk memperkenalkan topik-topik matematika kepada siswa. Topik-topik ini dipilih dengan dua pertimbangan, yaitu (1) aspek kecocokan aplikasi konteks dalam pengajaran, dan (2) kecocokan dampak dalam proses reinfention artinya prosedur, aturan, dan model matematika yang harus dipelajari, bukan diajarkan oleh guru tetapi siswa harus berusaha menemukan dan menampungnya dari masalah konstektual tersebut.
- Model dikembangkan sendiri. Prinsip ini berfungsi untuk menjembatani jurang antara matematika informal dengan formal dari siswa. Sewaktu mengajar contextual problem siswa mengembangkan model mereka sendiri. Sebagai konsekuensi dari kebebasan yang diberikan kepada siswa untuk memecahkan masalah memungkinkan muncul berbagai model hasil pemikiran siswa. Model tersebut diharapkan akan berubah dan mengarah kepada bentuk yang lebih baik dan efisien menuju kearah pembentukan pengetahuan formal.
Berdasarkan paparan di atas, berikut ini akan disajikan pembelajaran materi FPB dan KPK dengan mengorientasi siswa pada masalah kontekstual. Dari masalah ini kemudian siswa akan mengeksplorasi, membuat model-model yang sangat familiar dengan dunia mereka selama ini (matematisasi horizontal), dan pada akhirnya mereka akan dibimbing untuk menemukan konsep FPB dan KPK dari aktivitas-aktivitas yang mereka lakukan. Sebagai catatan bahwa FPB dalam bahan ajar ini dapat ditentukan dari banyak paket maksimum dan KPK dapat ditentukan berdasarkan penjumlahan dari hasil perkalian bilangan yang menunjukkan banyak masing kue dalam satu paket maksimum.
Adapun contoh pembelajaran matematika pada materi FPB dan KPK dengan Pendekatan PMR model penyajian makanan adalah sebagai berikut:
Di sebuah warung terdapat 15 kue bolu dan 60 kue timphan. Kue-kue tersebut akan disajikan kedalam beberapa piring sedemikian hingga isi tiap piring sama (banyaknya kue bolu di tiap piring sama begitu juga dengan kue Timphan)
Aktivitas 1
Dari konteks soal di atas kita dapat menyajkan paket-paket kue tersebut kedalam paket-paket makanan sebagai berikut. Untuk kue timphan disimbolkan dengan “t” dan kue bolu dengan “b”.
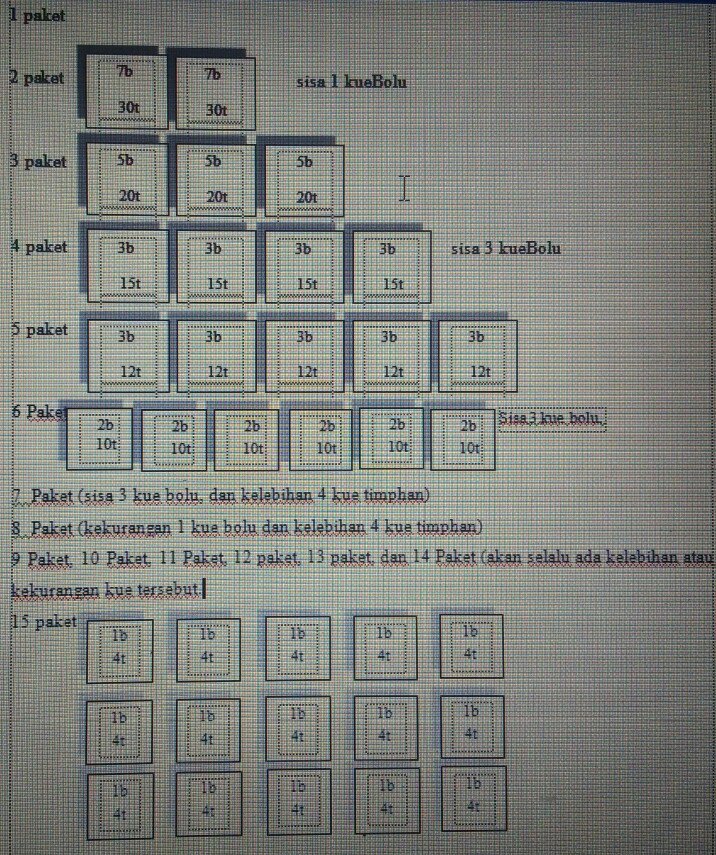
Aktivitas 2
Pisahkan kelompok paket-paket yang kue-kuenya tidak bersisa (yang memuat kue secara adil) dan kue-kuenya bersisa (kelebihan atau kekurangan kue). Selanjutnya fokuskan ke paket yang kue-kuenya tidak bersisa. Adapun paket-paket makanan yang memuat kue timphan dan kue bolu dapat dilihat pada penyajian berikut ini.
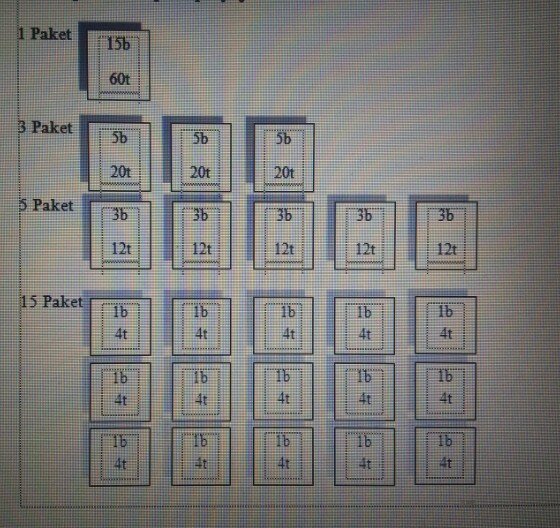
Berdasarkan penyajian di atas maka dapat diketahui bahwa 15 kue bolu dan 60 kue timphan di atas dapat disajikan dalam 1 paket, 3 paket, 5 paket dan 15 paket. Sedangkan penyajian kue dalam jumlah paket lainnya memberikan sisa kue timphan atau bolu dan bahkan juga kekurangan kue timphan ataupun kue bolu.
Aktivitas 3
Siswa akan menyelidiki beberapa pertanyaan berikut ini:
a. Berapa paket terbanyak yang bisa disajikan dari kue bolu dan kue timphan tersebut?
Dari pertanyaan di atas kita dapat memahami bahwa berdasarkan aktivitas 2 kita peroleh bahwa kue-kue tersebut dapat disajikan paling banyak kedalam 15 paket.
b.Berdasarkan point a. bagaimana kalau bilangan yang menunjukkan banyak kue bolu dan kue timphan pada satu paket dikalikan kemudian hasilnya dikalikan lagi dengan jumlah keseluruhan paket makanan (sajian paket terbanyak). Bagaimana hasil yang kalian peroleh?
Ada 15 paket makanan dan pada setiap paket memuat 1 kue bolu dan 4 timphan, maka hasil perhitungan dari bilangan tersebut adalah (1x4) x 15 = 60
c. Jika kemudian banyaknya sajian paket makanan dari 15 kue bolu dan 60 kue timphan dinamakan sebagai Faktor Persekutuan Terbesar (FPB) dan bilangan yang menunjukkan banyak kue bolu dan kue timphan pada satu paket makanan dari sajian paket terbanyak dikalikan kemudian hasilnya dikalikan lagi dengan jumlah keseluruhan paket makanan (sajian paket terbanyak). Tentukan FPB dan KPK dari15 dan 60?
FPB (15, 60) = 15 dan KPK (15, 60) = (1 x 4) x 15 = 60
Aktivitas 4
Pada aktivitas ini siswa mencoba untuk membuat kesimpulan berdasarkan aktivitas-aktivitas yang telah dilakukan di atas mengenai FPB dan KPK dari dua bilangan.
Adapun konsep FPB dari penyajian tersebut dapat ditentukan dengan mengambil sajian kue yang paling banyak yang bisa dipaketkan (Penyajian paket makanan paling banyak)
FPB 2 Bilangan = FPB (a, b) = Jumlah sajian paket maksimum/paling banyak
FPB (15, 60) = 15Adapun Konsep KPK dari penyajian tersebut dapat ditentukan dengan mengalikan bilangan yang menunjukkan banyak masing-masing kue pada satu paket maksimum dikalikan dengan jumlah paket makanan maksimum.
KPK (15, 60) = (1 x 4) x 15 = 60
Dari penyajian masalah di atas kita dapat memahami bahwa siswa diajak untuk memahami permasalahan kontekstual yang sangat familiar dengan kehidupan mereka, baru kemudian dari permasalahan siswa mencoba menyelesaikan soal-soal dari dunia nyata dengan cara mereka sendiri, dan menggunakan bahasa dan simbol mereka sendiri. Dari model yang telah di manipulasi kepada siswa kemudian diarahkan kepada model-model matematika. Kalau dengan pembelajaran sebelumnya siswa harus dipaksakan untuk menghafal rumus-rumus yang telah ditetapkan oleh para ahli sebelumnya, yang belum tentu sesuai dengan taraf perkembangan siswa. Akan tetapi dari pembelajaran yang telah disajikan membuat siswa seolah-olah menemukan rumus itu sendiri.
Lebih lanjut hal ini menjadi sebuah dasar bagi seorang pengajar yang akan mengajar materi FPB dan KPK seyogianya dalam proses pembelajaran (tidak hanya sekadar diawal pembelajaran) untuk dapat menyajikan masalah-masalah yang serupa seperti yang telah dipaparkan di atas. Hal ini dimaksudkan agar pembelajaran dapat lebih bermakna dalam kehidupan siswa.
Berdasarkan pembahasan di atas, dapat dipahami bahwa pembelajaran matematika dengan Pendekatan PMR model penyajian paket makanan pada materi FPB dan KPK sangat cocok untuk diterapkan dalam proses pembelajaran matematika di sekolah dasar. Kecocokan ini dirasakan sangat tepat apalagi pada permulaan siswa belajar memahami konsep FPB dan KPK. Selain pembelajaran seperti ini akan mendekatkan siswa dengan kehidupannya, juga akan memberikan kesan kepada siswa bahwa belajar matematika itu sangat mengasyikkan dan juga merupakan sarana bagi mereka untuk berlatih dalam mengaplikasikan konsep matematika dalam kehidupan nyata mereka. Selain dari itu belajar dengan cara demikian akan membuat siswa seolah-olah menemukan kembali ide-ide matematika yang sedang dipelajari.
Di sisi lain, mengajarkan bahan ajar ini, kepada siswa berarti ikut mendukung usaha pengembangan pendidikan matematika realistik yang sedang digalakkan saat ini. Dengan demikian kesukaran dan ketidakbermaknaan matematika pada materi FPB dan KPK yang dirasakan sulit oleh manyoritas siswa sekarang kita harapkan dapat berkurang. Lebih lanjut penerapan bahan ajar ini akan lebih memposisikan guru sebagai fasilitator belajar, guru telah mampu membangun pengajaran yang interaktif, guru telah memberi kesempatan kepada siswa untuk aktif memberi sumbangan pada proses belajarnya, guru harus telah membantu siswa dalam menafsirkan masalah-masalah dari dunia nyata; dan guru telah proaktif mengaitkan kurikulum matematika dengan dunia nyata, baik fisik maupun sosial.
Good idea pak @fachrurazi. Arifka kemaren baru bhas tntang kpk dan fpb, tapi msih menggunakan prosedural yg lama 😁
Silahkan di pahami kembali tulisan bapak, mudah-mudahan dapat bermanfaat untuk mengajar fpb dan kpk kali yang akan datang. Ikuti aja langkah-langkahbyang sudah bapak gambarkan dalam tulisan ini dan gunakan media gambar makanan dan piring persis seperti di gambar.
Mantap kali lah bila suatu masalah dibedah oleh para pakarnya. Terus berkarya @fachrurazi dan promosi kan akun nya utk mahasiswa. Ilmu matematika nya sangat okee.
Salam kenal @danisyarknai
Alhamdulillah, masih dalam tahap belajar juga prof. Terima kasih atas semangat dan motivasi dari prof.