
문제의 해결

하릴없이 눈을 뜨긴 하였으나, 마땅한 대책이 있는 것은 아니었습니다. 어째서 당대를 대표하는 위대한 과학신들이 쓸모없는 이야기만 늘어놓다 가셨을까요. ‘모르겠다’라는 답을 내놓아야 하는 착찹한 마음을 가다듬으며 문제를 다시 보았습니다.
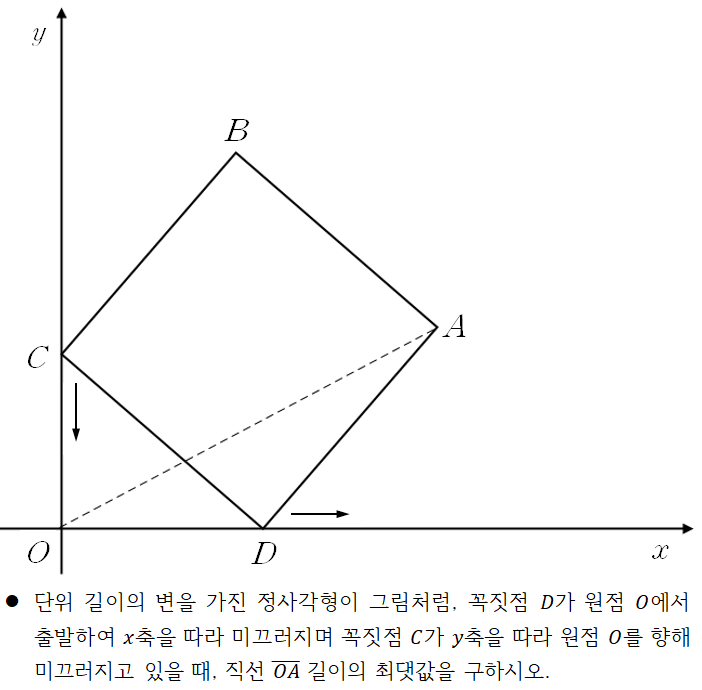
앞이 깜깜했습니다. 이런 문제를 두고,
“지나치게 복잡하고 난해한 풀이는 고정된 관점의 문제일 수 있다”
“자신을 기준으로 본 세상에서 벗어나 다른 기준으로 세상으로 보았을 때, 또 다른 진실을 발견할 수 있다”
라니, 뜬구름 잡는 소리나 한 과학신들이 야속했습니다.
“선생님, 다른 방법이 없나봐요?”
마침내 학생들이 재촉하기 시작하였습니다.
“그래, 아무래도 이 문제는 계산력으로 푸는...엇!”
포기의 선언을 하려던 순간, 불현듯 머릿속에 광명이 비치며 코페르니쿠스와 아인슈타인의 가르침에서 한가지 공통점이 떠올랐습니다. 코페르니쿠스는 기존에 지구를 중심으로 좌표를 설정하여 복잡해진 천체의 운행을 태양으로 그 중심을 옮김으로서 간명하게 설명할 수 있었고, 아인슈타인은 움직이는 전하에 가해지는 자기력이라는 힘이 사실은 전하의 시점으로 보면 전기력과 같음을 밝혀 내었었습니다. 다시 말해, 그들은 자신이라는 기준틀에서 벗어나 상대를 기준으로 삼음으로써 새로운 발견을 이끌어 내었던 것입니다.
아아, 알 것 같았습니다. 그들은 O점이 아닌, □ABCD의 시점에서 문제를 다시 보라고 말하고 싶었던 것입니다. 아마 신들에게도 직접적인 관여는 불가하다는 규칙이 있어, 이렇게 에둘러 가르침을 준 모양이었습니다. 무당마다 점괘가 달라지고 해석이 달라졌던 것이 이해가 갔습니다.
그렇다면 □ABCD를 고정하면 점 O는 어떻게 움직일 것인가. 여기서부터는 그다지 어려운 문제가 아니었습니다. ‘직교’좌표계의 원점이었던 O는 △OCD에서 항상 직각을 이루며 움직이는 까닭이었습니다. 저의 새로운 풀이는 다음과 같았습니다.

그림 1에서 선분 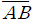 를 지름으로 하는 원 위에 한 점 C는 언제나 ∠ACB를 직각으로 하는 직각삼각형 △ABC을 이루고, 역으로
를 지름으로 하는 원 위에 한 점 C는 언제나 ∠ACB를 직각으로 하는 직각삼각형 △ABC을 이루고, 역으로 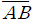 를 빗변으로 하는 직각삼각형 △ABC의 꼭짓점 C도 반드시
를 빗변으로 하는 직각삼각형 △ABC의 꼭짓점 C도 반드시 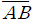 를 지름으로 하는 원 위에 존재하는데, 주어진 문제에서도 마찬가지로 □ABCD를 고정한 경우 점 O가
를 지름으로 하는 원 위에 존재하는데, 주어진 문제에서도 마찬가지로 □ABCD를 고정한 경우 점 O가 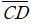 를 빗변으로 하는 직각삼각형 △OCD를 이루며 움직이므로, 점 O의 자취는 점 D에서 C로 움직이며 반원을 그립니다. 아래의 그림 2는, 정지한 좌표계 위에서 □ABCD가 움직이는 모습과 사각형 □ABCD이 정지했을 때 점 O가 움직이는 모습을 보여줍니다.
를 빗변으로 하는 직각삼각형 △OCD를 이루며 움직이므로, 점 O의 자취는 점 D에서 C로 움직이며 반원을 그립니다. 아래의 그림 2는, 정지한 좌표계 위에서 □ABCD가 움직이는 모습과 사각형 □ABCD이 정지했을 때 점 O가 움직이는 모습을 보여줍니다.
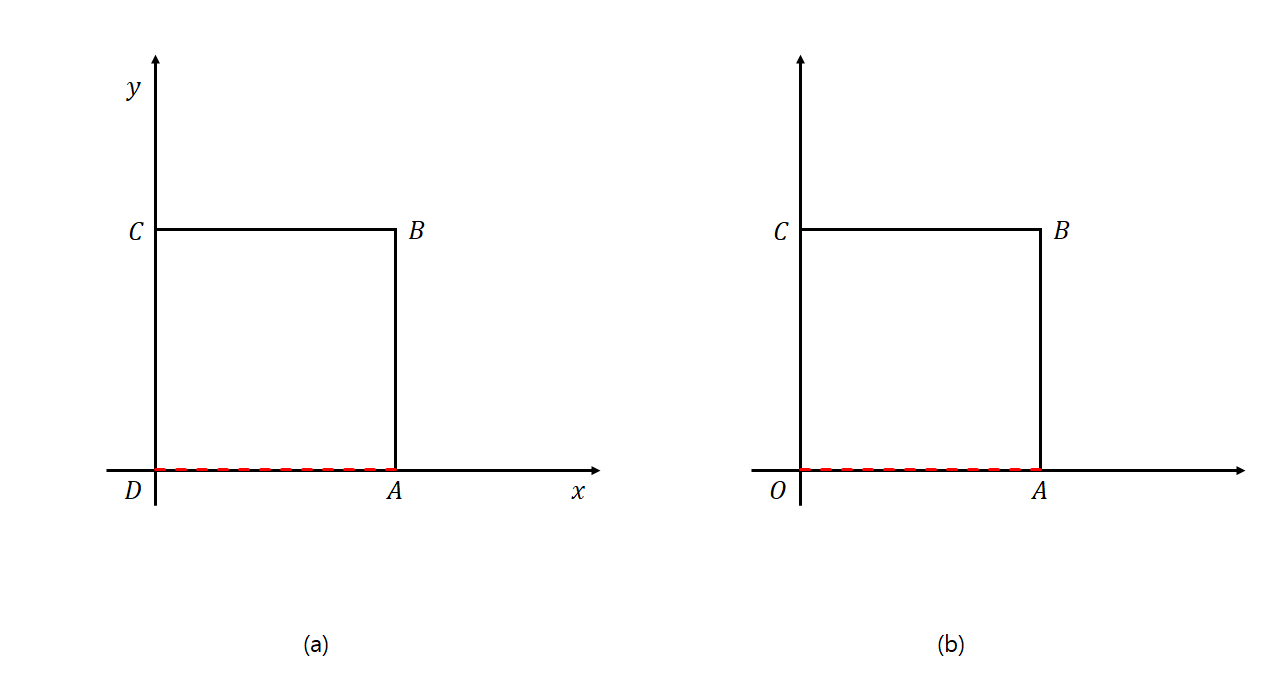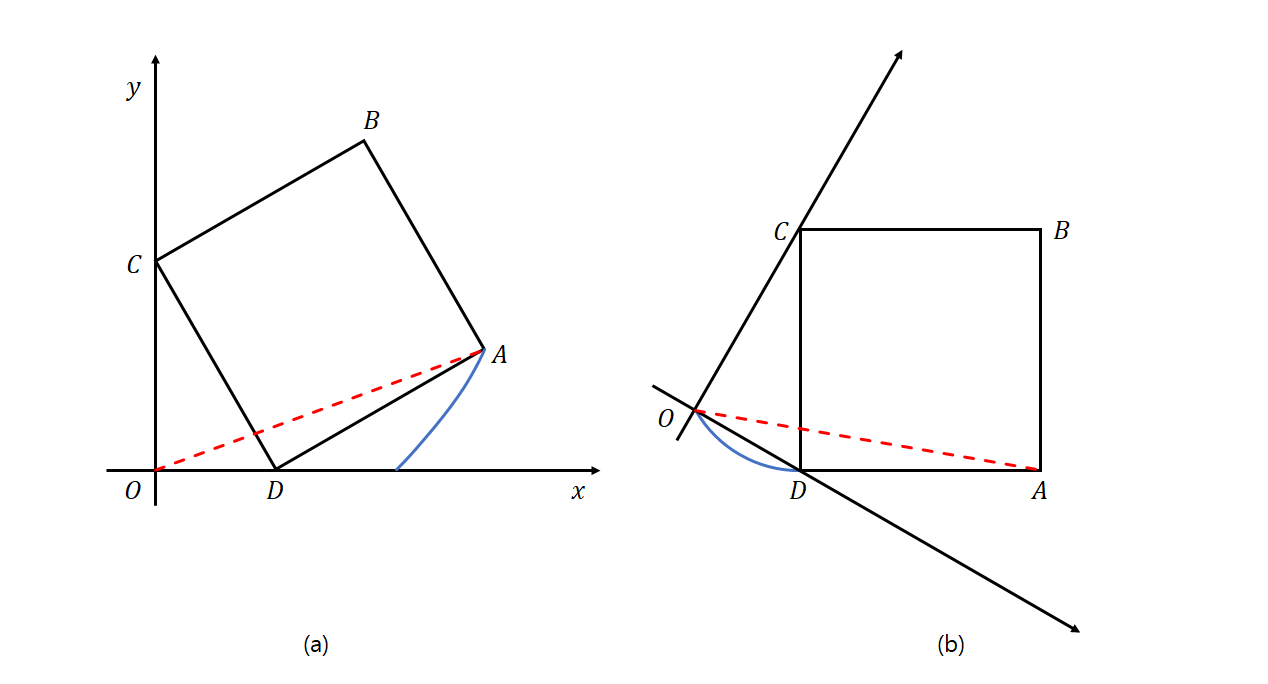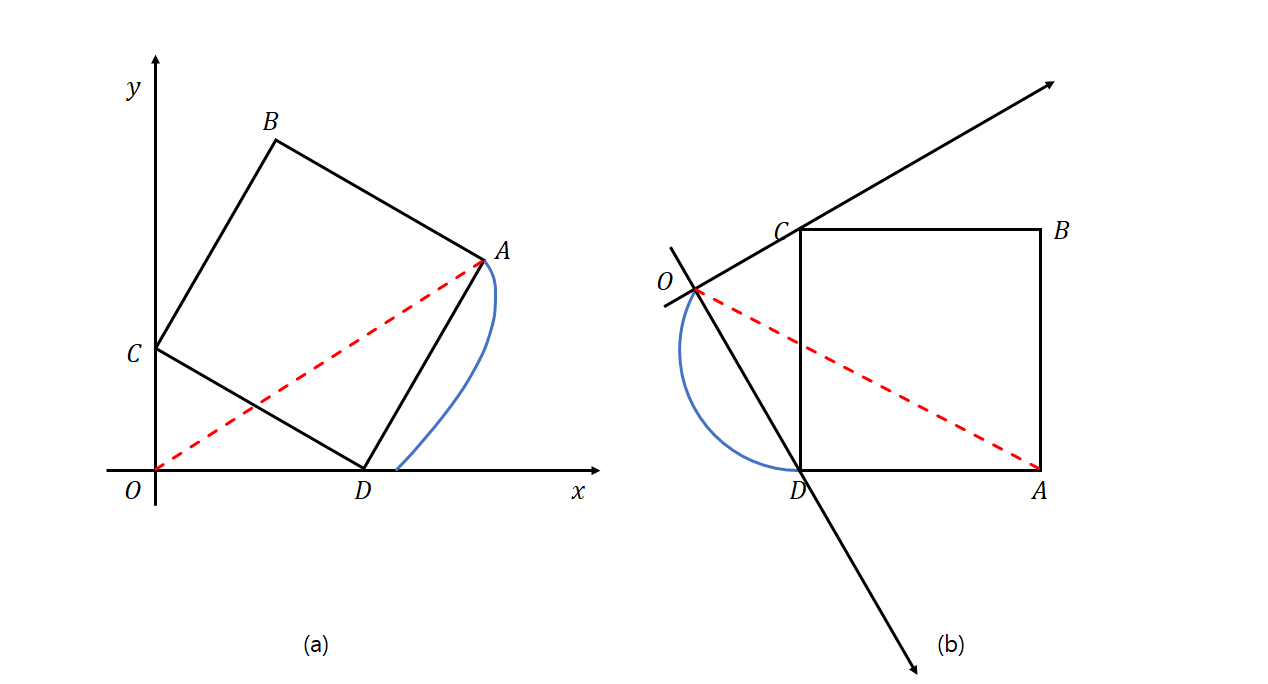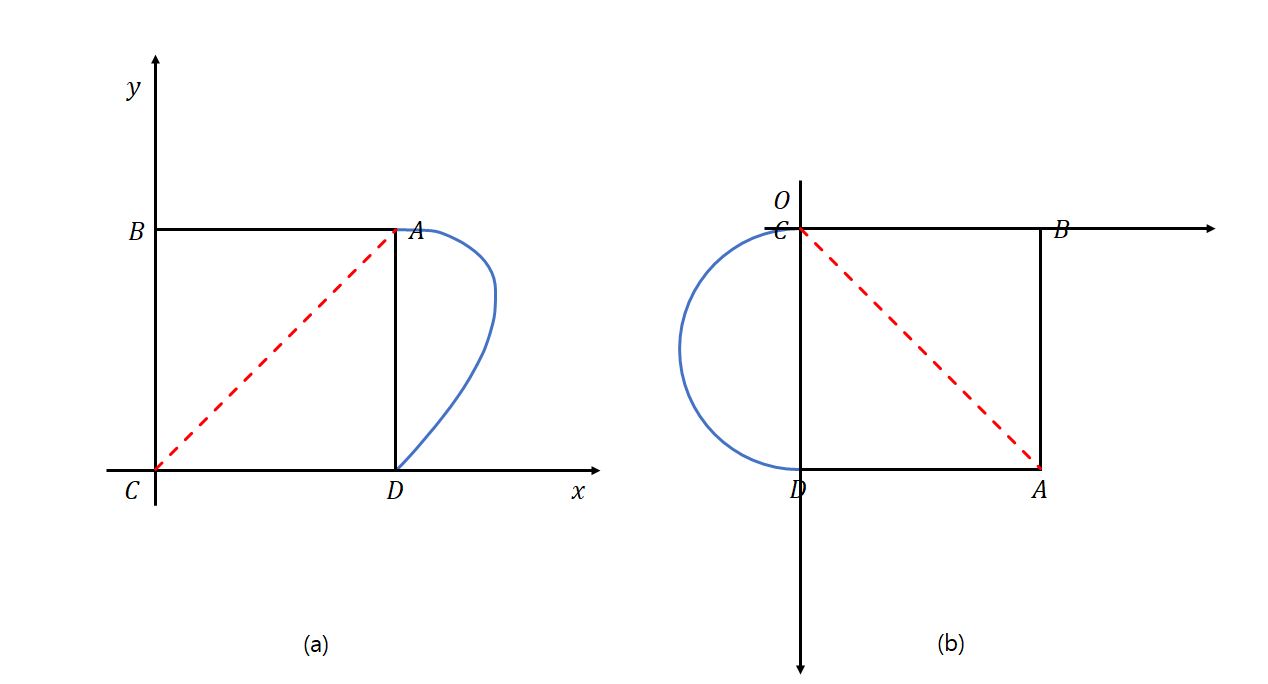
이제 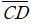 를 x축 위에 놓은 새로운 좌표계는 다음과 같습니다.
를 x축 위에 놓은 새로운 좌표계는 다음과 같습니다.

이 때, 삼각형의 한 변의 길이는 다른 두 변의 길이의 합보다 반드시 작으므로, 삼각형 △OO'A에서 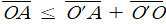 의 관계식을 얻을 수 있고,
의 관계식을 얻을 수 있고, 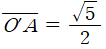 ,
, 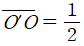 이므로
이므로 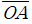 의 최댓값
의 최댓값 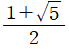 를 바로 얻을 수 있습니다!
를 바로 얻을 수 있습니다!
또 만약, 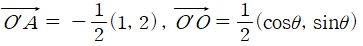 로 두고 푼다손 하여도,
로 두고 푼다손 하여도,
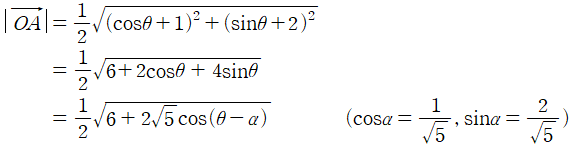
이므로, 최댓값 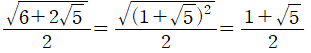 이 단 세 줄의 수식만으로 도출됩니다.
이 단 세 줄의 수식만으로 도출됩니다.
이는 이전의 풀이와 달리 좌표점도 설정할 필요도, 미분을 하지 않아도 되는, 암산이 가능할 정도로 손쉬운 풀이였습니다. 일부러 수식을 써도 이전과는 비교도 할 수 없이 빠르고 정확하게 답을 구할 수 있었습니다.
“얘들아, 선생님은 이 정도 문제는 암산으로도 풀 수 있단다.”
어깨에 잔뜩 힘이 들어간 저는 학생들에게 새로운 풀이법을 가르쳐주었습니다.
“알겠니? 풀이의 발상은 간단하단다. 첫째, 지나치게 복잡하고 난해한 풀이는 고정된 관점의 문제일 수 있다! 둘째, 자신을 기준으로 본 세상에서 벗어나 다른 기준으로 세상으로 보았을 때 또 다른 진실을 발견할 수 있다!”
마치 제가 코페르니쿠스나 아인슈타인이 된 듯한 기분이었습니다. 학생들도 신선한 발상에 수학적 감성이 한껏 고양되었을 듯하여 마음이 뿌듯했습니다.
그런데 막상 학생들의 표정은 너무 덤덤하고 오히려 마뜩지 않아 보였습니다.
“이해가 잘 안 되니? 왜 표정이 별로야?”
“선생님, 그런게 아니고요. 저희는 저런 생각을 할 수 없어요. 배운다고 쓸 수 있는게 아니예요.”
다소 충격적인 답변이었습니다. 결국 그들은 저에게 기계적인 풀이법을 바랐던 것입니다. 우수반이라는 학생들마저 자신의 한계를 규정하고 있다는 사실이 이내 제 마음을 답답하게 만들었습니다. 또 한창 자유로운 생각을 발산하길 원할 학생들이 교육 제도 아래서 정형화되고 표준화된 풀이를 원한다는 사실에 서글퍼졌습니다. 지금의 교육이 학생들을 산수하는 기계로 전락시켜버린 것은 아닐는지, 학생들에게 생각할 용기를 북돋아 줄 교육이 필요해 보였습니다.
그러나 한편으로는 비단 교육제도의 탓 뿐이 아니라, 인간의 본성상 기계적 풀이를 더 바라는 것도 같았습니다. 개인 교습을 해보면 학생들은 늘 단원 밖의 두 번째 풀이에는 관심이 없고, 암기할 공식만을 요구하곤 하는데, 오늘의 학생들도 그저 평범한 학생들이었을 따름인 것입니다. 안타깝게도, 학생들은 발상을 강조하는 선생보다 암기를 강조하는 선생을 선택함으로써 스스로 몰개성의 길을 걷고 있는지도 모릅니다. 성인이 되어서는 누구나 획일화된 교육제도를 비판하지만, 정작 학생일 때에는 획일화의 안락함을 추구하는 셈입니다.
닭이 먼저인지 달걀이 먼저인지 모를 이 문제에서, 우리는 과연 자신의 편안한 틀을 벗어나 코페르니쿠스적 전환을 이끌어낼 수 있을까요. 수학 문제를 기쁘게 풀고 나니, 풀지 못할 사회 문제로 바뀌어 버린, 착잡한 마음으로 끝난 수업이었습니다.
P.S. 과학신님들 Thank you!
(마침)
저자의 다른 글
과학 에세이
● 양자역학, 경제학, 그리고 진화론 (1)● 양자역학, 경제학, 그리고 진화론 (2)
● 교양을 위한 양자역학 (1)
● 교양을 위한 양자역학 (2)
● 여러분이 가장 먼저 배운 제2언어는 무엇입니까?
● 미래에는 음성 언어가 사라질까? (1)
● 미래에는 음성 언어가 사라질까? (2)
● 미치오 카쿠가 말하는 양자 컴퓨터
● 카쿠와 마윈이 말하는 미래
● 종 예외주의 (1) : 들어가며
● 종 예외주의 (2) : 종의 분화
● 종 예외주의 (3) : 이기적인 종
● 종 예외주의 (4-1) : 이타적인 종 ; 정의란 무엇인가
● 종 예외주의 (4-2) : 이타적인 종 ; 도덕적 동물
● 종 예외주의 (5-1) : 이기와 이타의 경계 ; 선과 악의 공존
● 종 예외주의 (5-2) : 이기와 이타의 경계 ; 이기와 이타의 진화 上
● 종 예외주의 (5-2) : 이기와 이타의 경계 ; 이기와 이타의 진화 中
● 종 예외주의 (5-2) : 이기와 이타의 경계 ; 이기와 이타의 진화 下
● 종 예외주의 (5-3) : 이기와 이타의 경계 ; 동전의 양면
● 종 예외주의 (6) : 마치며
● 사고의 코페르니쿠스적 전환 (1)
● 사고의 코페르니쿠스적 전환 (2)
● 사고의 코페르니쿠스적 전환 (3)
● 사고의 코페르니쿠스적 전환 (4)
● 교양을 위한 양자역학 (1)
● 교양을 위한 양자역학 (2)
● 여러분이 가장 먼저 배운 제2언어는 무엇입니까?
● 미래에는 음성 언어가 사라질까? (1)
● 미래에는 음성 언어가 사라질까? (2)
● 미치오 카쿠가 말하는 양자 컴퓨터
● 카쿠와 마윈이 말하는 미래
● 종 예외주의 (1) : 들어가며
● 종 예외주의 (2) : 종의 분화
● 종 예외주의 (3) : 이기적인 종
● 종 예외주의 (4-1) : 이타적인 종 ; 정의란 무엇인가
● 종 예외주의 (4-2) : 이타적인 종 ; 도덕적 동물
● 종 예외주의 (5-1) : 이기와 이타의 경계 ; 선과 악의 공존
● 종 예외주의 (5-2) : 이기와 이타의 경계 ; 이기와 이타의 진화 上
● 종 예외주의 (5-2) : 이기와 이타의 경계 ; 이기와 이타의 진화 中
● 종 예외주의 (5-2) : 이기와 이타의 경계 ; 이기와 이타의 진화 下
● 종 예외주의 (5-3) : 이기와 이타의 경계 ; 동전의 양면
● 종 예외주의 (6) : 마치며
● 사고의 코페르니쿠스적 전환 (1)
● 사고의 코페르니쿠스적 전환 (2)
● 사고의 코페르니쿠스적 전환 (3)
● 사고의 코페르니쿠스적 전환 (4)
신경 과학
● 기억이란 실제로 무엇일까?● 마음을 드러내는 방법 : 마음 챙김 명상의 철학과 신경 과학
● 양자 역학이 의식의 본질을 밝혀낼 수 있는 이유
● 신경 가소성 : 내가 나를 보는 방식
● 양자 역학이 의식의 본질을 밝혀낼 수 있는 이유
● 신경 가소성 : 내가 나를 보는 방식
본문의 생각하는 방식이 패턴의 하나로 머릿속에 들어가겠네요..
공학수학 배울 때 일단 외우고 나서 생각하라던 교수님 말씀이 생각납니다 ㅋㅋㅋ
이 말씀을 들으니, 슈뢰딩거 방정식 푸는거 자체는 별 의미가 없다고, 그래서 나온 해가 무슨 의미냐고 묻던 교수님이 떠오릅니다. 본인은 방정식을 안풀어도 해의 꼴을 알 수 있다시며, 식은 알고 있는걸 기술하는 수단이라고... 수강신청 기피대상으로 유명하셨습니다ㅎㅎㅎㅎ
고맙습니다. 왕자님.!!! 자괴감을 멈출수 있어서요.ㅋㅋㅋ
사실 전에 댓글을 추적하다가 결론을 봐서 답은 알고 있으나, 과학신들의 사설에 4회까지 부족함을 뼈저리게 느꼈네요. ㅋㅋㅋ
수식은 배웠어도 조금만 지나면 금방 잊어버리죠ㅜㅜ 물리는 한동안 하지말아야겠어요
자신을 기준으로 본 세상에서 벗어나 다른 기준으로 세상으로 보았을 때 또 다른 진실을 발견할 수 있다는 말이 과학이 아닌 다른 분야에서도 적용되지 않을까 싶어요 글 잘 읽고 갑니다. ㅎㅎ
네 독자들에게 그러한 메시지 또한 전달하고 싶은 마음에서 뭉뚱그려 적어보았습니다ㅎㅎ 긴 글 보아주셔서 감사합니다.
이번 건 좀 쉽네요 ㅋㅋ 학교다닐 때도 도형 문제 좋아했죠~
대학교에서도 눈에 보이는 조금은 거시적인 재료역학 구조역학 요런 것들은 재밌게 했었죵 ㅋㅋ 반면 열역학 전지전자공학"기초" 처럼 눈에 잘 안 보이는 건 애먹었습니다 ㅋㅋㅋ ㅜㅜㅜ 지금도 친하지 않아요.. 회사에서 연비=에너지 효율 극대화 일을 하다보니 열에너지전기와 떼어놓을레야 뗄수가 없어요.. 그래서 결론은 얼른 회사를 졸업해야겠다......? ㅋㅋ 입니다.
진짜 그 놈의 "기초", "입문"ㅋㅋㅋㅋㅋ
도형 참 재미있는데, 정규교육과정 내에서 도형 문제는 중학교가 마지막이라 조금 아쉬운 감이 있습니다. 이 문제도 결국 중학교 수준의 도형 지식만으로 풀 수 있는 문제였습니다.
학생들은 여유가 없어서 그럴 거라고 생각합니다^^;
이거 풀고 다른거 풀어야 하는데, 다른 과목해야 하는데..
이런 생각을 하겠죠. 정작 인생을 꼭 그런 것이 아닌데 말입니다-
이게 제가 20대 중반의 일인데, 저도 불과 몇년전까지 학생이었던만큼 이해 못하는 바도 아니었지만, 저도 겪었던 시기이니만큼 안타깝기도 했습니다.
그리고 과외하면서 다양한 학년의 학생들을 가르쳐보니 꼭 학습량이 빡빡해서 그런것만은 아니더라고요. 기본적으로 편하게 암기하려드는 습성이 있었습니다. 그래서 학생들의 창의력을 증진시키는 교육이란 것이 참으로 어렵구나 생각이 들었습니다.
또 이렇게 하나의 시리즈를 마무리 하였군요. 축하합니다!
감사합니다! 글은 짧은데 제가 게을러서 기간만 늘어졌습니다ㅎㅎ
본문의 내용을 잘못 보신 것 같습니다. 저는 말씀처럼 다양한 생각방법, 다양한 풀이 방법을 모두 공부하고, 비교 검토하여, 다양한 방법이 같은 답을 내는지와, 어떤 방법이 가장 효과적인지 등을 비교 검토 해야 한다고 보는 입장으로 이 글을 쓴 것입니다.
제가 학생들에게 이렇게 문제를 다르게 보는 방식도 있다고 소개했더니, 학생들은 기존의 획일화된 풀이 방식을 원하더라, 하는 아쉬움을 표현하는 글이었습니다. 이 시리즈의 첫 글을 보시면 기존의 교과서적인 풀이가 얼마나 복잡한지 보실 수 있습니다.
재미있게 보아주셔서 감사합니다.