[Reivew #2 책+영화] 어느 수학자의 변명 + 무한대를 본 남자 ,부제 : 모든 자연수의 합은 -1/12??

안녕하세요.

오늘은 특별한 포스팅을 준비해봤습니다. 얼마전 @beoped님이 작성하신 제타함수에 관한 포스트를 보고

https://steemit.com/kr-math/@beoped/4y2cst

영감을 받아서 준비한 책과 영화 리뷰입니다. 책 제목은 "어느수학자의 변명"이며 영화는 "무한대를 본 남자"입니다.

언뜻 보기에 두 책과 영화 그리고 @beoped님이 말씀하신 제타함수가 어떤 관계가 있는지 궁금하실 텐데요? 바로 3가지 토픽 모두 인도의 천재 수학자 스리니바사 라마누잔과 연관이 있다는 공통점이 있습니다.

짤막하게 라마누잔은 누구인가? 인도 출신의 수학자로 어릴적부터 신동으로 자랐지만 제대로 된 수학교육을 받은 적이없었습니다. 하지만 스스로 수학을 독학하였고 (그 증거로 우리가 흔히 알고 있는 이차 방정식의 일반해를 독자적인 형형태로 유도해서 썻다고 하네요.) 이후 그의 천재성을 알아본 캠브릿지 대학교의 교수 하디가 제자로 거두어 둘은 정수론에 지대한 공헌을 하였습니다.

==============================================================================

책 리뷰 - 어느수학자의 변명

한글 버전

영문 버전

이책은 영국의 저명한 수학자 고드프리 해럴드 하디의 회고록입니다. 본 책에서 하디는 자신이 사랑하는 순수수학의 가치, 존재 이유, 아름다움을 적나라하게 표현하고 있는데요. 그 표현이 너무나도 직설적이라 조금 충격적이기도 합니다. 예를 들어 그는 순수수학이 아닌 우리 인류의 편리와 일반인들의 교육을 위해 개발되고 연구되어지는 모든 응용수학을 쓰레기라고 치부하는데요. 그러면서 자신에게 순수수학을 연구하는 이유와 그 가치를 물을 때는 순수수학은 그 존재자체로 고귀하고 가치가 있는 것으로 연구목적과 그 응용을 생각할 필요가 없다고 말합니다. 언뜻 보기엔 굉장히 오만하고 다른 응용학문을 낮추어 본다고 생각할 수 있겠는데 그만큼 순수수학에 대한 하디의 사랑과 열정을 엿볼수 있는 대목입니다.

그렇다면 책의 제목인 변명은 어떤 의미에서 쓰여진 걸까요? 이 책을 썼을 떄 하디는 예순을 넘긴 시점이었는데요. 그만큼 수학적인 직관과 사고능력 뿐만 아니라 문제를 대하는 집중력도 많이 떨어졌겟죠? 위에서 말한것처럼 그토록 사랑하던 수학을 대하는 자세가 예전같지 않음에 대한 슬픔과 처참하게 느끼는 자신의 현실을 고백합니다. 그러면서 앞선 시대의 존경받는 대학자 뉴튼, 오일러 등도 그들의 모든 업적이 20대에 완성되었다며 현재 자신의 상황을 위로, 변명합니다.

이런 그를 겸손하게 만들고 인정할 수 밖에 없었던 동료 3명이 소개되는데 바로 상대성이론의 천재물리학자아이슈타인, 캠브릿지의 동료 리틀우드 그리고 마지막이 바로 라마누잔입니다. 자신은 리틀우드와 라마누잔이 없었다면 지금의 업적은 없었을거라고 말하고 있습니다. 그리고 라마누잔과의 만남은 너무도 아름다운 운명이었다고 말하고 그를 진정한 친구였다고 설명하는데 당시 인도가 영국의 지배를 받고 있었고 두 사람 사이의 신분차이를 고려했을 때 그는 학문내에서 철저한 배척과 차별을 하였지만 인간 자체에는 차별주의자가 아니었던것 같네요

==============================================================================
영화 리뷰 - 무한대를 본 남자

어느 수학자의 변명이 하디의 입장에서 라마누잔의 얘기를 한다면 무한대를 본 남자는 주인공이 바로 라마누잔입니다. 인도에서 독학하여 우연한 기회에 하디를 만나 캠브릿지를 가고 생의 마지막까지 수학을 고민하는 내용입니다. 이 영화에서 묘사된 그리고 실제의 라마누잔이 그러하듯이 그는 매우 뛰어난 통찰력과 직관을 가진 천재입니다. 그래서 현대수학에 대한 지식이 거의 없음에도 불구하고 직관만으로 여러 문제등을 풀어내죠. 특히 연분수 ( 분수가 연속적으로 나타나는 형태)나 무한수열에서 그의 직관은 탁월한 능력을 발휘합니다.

하디는 이런 그의 천재적인 능력을 알아보고 캠브릿지에서 기초적인 단계부터 엄밀하게 이론을 증명하는 과정을 배우게 합니다.

기억이 나는 장면으로는 그가 다른 교수의 수업중 필기를 하지않자 교수가 라마누잔에게 질문을 하였고 막힘 없이 답을 대답합니다. 곧바로 교수가 왜 그렇냐고 물으니 라마누잔은 "그냥 저는 알아요"라고 대답하죠. 라마누잔은 정말 직관적으로 그 문제의 답을 알아낸 거였지만 교수는 심한 모욕감을 느끼고 그에게 버럭 화를 냅니다. 라마누잔 역시 자신에겐 당연한 문제들을 왜 귀찮고 복잡한 과정을 통해 증명해야하는지를 이해못하고 이런 문제로 하디와 잠시 갈등을 겪기도 합니다. (이래서 똑똑한 사람이 아닌 적당히 똑똑한 사람이 과외를 해야 더 잘 가르치는 것 같습니다. 어려운 점을 공감할 수 있으니까요 ㅎㅎ)

사실 영화자체만을 놓고보면 꽤나 지루한 영화입니다. 하지만 수학을 좋아하시는 분들에겐 충분히 시간때우기에 좋은 영화라고 생각되네요 ㅋ

==============================================================================

마지막으로 하디가 풀어낸 재미있는 문제를 소개하도록 하겠습니다. 사실 이 이야기를 하고 싶었는데 이것만 하기에는 너무 내용이 빈약해 관련된 책과 영화까지 소개했네요 ㅎㅎ

@beoped님의 포스트에도 잠시 소개되었지만 제타함수의 -1에서의 값은 -1/12입니다. 달리 말하자면

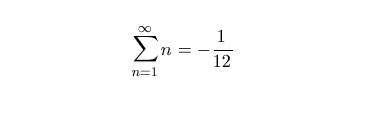
모든 자연수의 합은 -1/12이라는 것입니다!!!! 당연히 무한대로 발산해야할 자연수의 합이 수렴을 한다는 것도 신기한데 그 값이 음수라니?? 정말 알쏭달쏭합니다.ㅎㅎ

하지만 위 관계는 특정한 수학적 관점에서 분명히 valid한 수식입니다. 실제로 우주물리분야에서 @beoped님이 잠시 언급하셨지만 string theory에서 중요하게 쓰이는 수식이기도 하구요.

그럼 왜 이렇게 되는지 한번 볼까요 ?

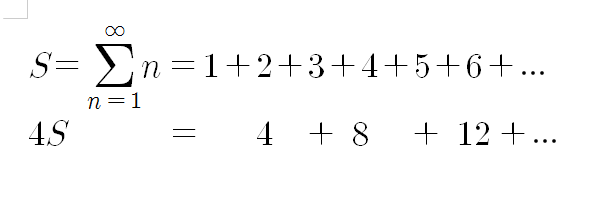
먼저 우리가 구하고자 하는 자연수의 합을 S라고 정의하고 그것의 4배를 한뒤 첫번째 식에서 2번째 식을 뺴면

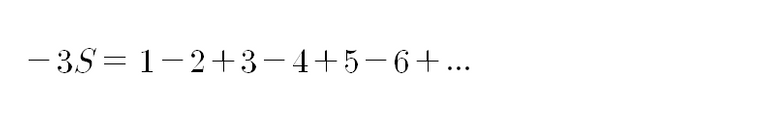
다음과 같이 됩니다. 그리고 이를 다시 아래와 같이 잘 배열해서 더해주면

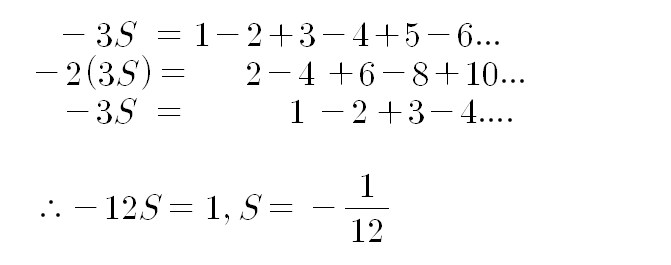
간단히 우리가 원하는 결과를 도출할수있습니다.!

하지만 사실 위의 증명은 틀렸습니다. 왜냐면 (무한대 –무한대)의 정의되지않는 연산을 하기 때문입니다.

이를 엄밀히 증명하는 스텝은 전문적인 수학지식이 필요하므로 스킵하고 대강의 outline만 적겠습니다.

1. 리만제타 함수에 Gamma function 을 곱한다.
2. 이렇게 곱한 함수는 analytic function이 되고 이를 analytic continuation을 통해 실수부가 -1인 domain까지 확장
3. -1을 대입한뒤 -1/12을 도출!

위 과정에서 anayltic continuation, Cauchy's residue theorem같은 수학적인 이론들이 필요로 합니다.

그리고 @gogumacat 님의 말씀처럼 리만제타 함수는 리만가설로 유명한 소수 정리와 깊은 연관이 있습니다. 아마 스티밋의 많은 능력자분 한분께서 언젠가는 이 주제도 다루지 않을까 싶네요 기대하겠습니다.

여기까지 포스팅을 마치겠습니다. 맛집 얘기만 하다가 지루한 토픽을 다루었는데 재밌게 봐주셨으면 좋겠네요~!