실제로 블록은 어떻게 구성돼 있을까?
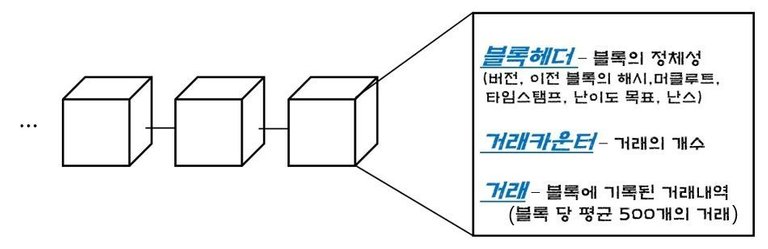
블록은 블록의 정체성을 띠는 데이터를 가진 블록헤더, 해당 블록에 거래의 개수를 알려주는 거래 카운터, 그리고 가장 많은 공간을 차지하는 거래목록들이 있다.
또 블록헤더를 3가지 구성으로 나눠보면 이렇게 된다.
현재 블록이 이전(previous) 블록과 연결 되어 있음을 나타내는 이전 블록의 해시값을 포함한다는 부분.
난이도, 타임스탬프, 난스. 이전 포스팅에 설명했듯 채굴 경쟁과 직접적 연관이 되는 부분.
3. 머클루트(Merkle Root)
1번은 블록이 이전블록과 연결되어있다는 것을 나타내는 것이며 해당 블록을 식별하는 것이고,
2번은 채굴자들이 연산을 통해 블록을 채굴하는데 연관된 것들인데
그렇다면 과연 3번. 머클루트란 무엇일까.
머클루트란 머클트리(쉽게 나무라고 생각하자)에서 뿌리 부분에 해당하는 것으로 해당 블록에 있는 모든 거래내역(수백에서 수천개 가량되는 거래량)을 요약하여 작은 사이즈의 용량으로 블록헤더에 존재하는 데이터이다.

그렇다면 블록 하나에서는 모든 거래내역을 가지고 있으면서도 왜 요약본을 더 가지고 있을까? 이것은 머클트리(Merkle Trees)를 알면 왜 머클루트(Merkle Root)가 헤더에 포함되며 왜 그것이 효율적인지 알 수가 있다.
그런데 머클트리(Merkle Trees)에 대해 찾아보면 다들 이진트리(binary trees)라는 표현을 써서 설명을 하고있고 영문으로 찾아봐도 비슷한 내용들 뿐인데 여기서 '이진트리'는 쉽게 말해서 거래를 두개씩 묶는다는 말이다.
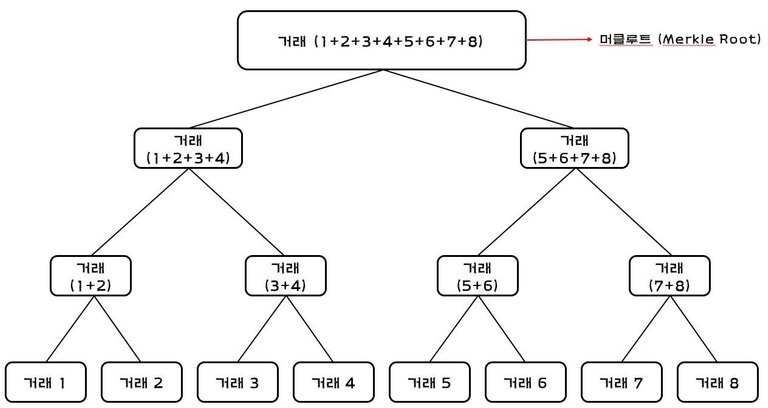
이 그림이 머클트리(Merkle Trees)이다. 나무를 뒤집어 놓은 모양이라고 생각하자.
그림은 가장 단순하게 8개의 거래로 묶어 예를 든것인데, 8개 뿐만 아니라 몇 개의 거래 데이터가 있든 하나의 뿌리(루트)로 만들어 준다.
이 과정은 그림처럼 두 개씩 거래를 묶은 다음 SHA256 알고리즘을 통해 해시값으로 나타내고 또 그렇게 묶은 값들을 다시 두 개씩 묶어서 또 해싱하여 수 백개의 거래 값들을 그림의 가장 꼭대기에 위치한 하나의 데이터로 만들어주는 것이다. (거래가 몇 십개든 몇 백개든 몇 천개든 뭉쳐서 요약된 머클 루트의 용량은 32바이트로 항상 같다.)
이렇게 두개씩 묶어서 올라가면 좋은점이 거래량이 기하급수적으로 늘어나도 특정 거래를 찾는 경로는 단순하다는 것이다.
거래의 건수인 N이 증가할 때마다 특정 거래의 경로를 찾는 경우의 수는 log2(N)으로 늘어나기 때문이다. (여기서 log 스케일이 2인것은 거래를 두 개씩 묶어서 올라가기 때문.)
갑자기 로그가 나온다고 어렵게 생각하지말고 밑의 그림을 보자.
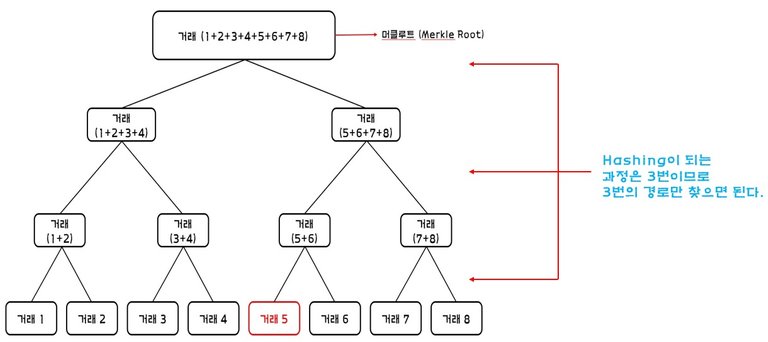
만약 빨갛게 표시된 <거래 5>를 찾으려고 할때 위 그림을 보면 해싱이 되는 과정이 세 번이 었으므로 세 번의 경로만 찾아가는 연산을 하면 <거래 5>를 빠르게 찾을 수 있다.
그림처럼 8개의 거래가 아닌 1024개의 거래라고 해도 거래량이 대폭 는 반면 경로는 열 번(log2[1024]=10)으로 찾아가는 연산으로 특정 거래 데이터를 쉽게 찾을 수 있다는 원리를 이용한 것.
그렇기에 거래 내역을 위조하려는 시도가 있어도 머클트리의 경로를 따라가면 해시값이 다른 것이 나오게 되어 금방 거래의 위변조도 알 수있게 되고 이를 방지할 수 있다.
블록체인의 용량은 시간이 지날수록 지속적으로 늘어가기 때문에 이제는 성능이 좋은 컴퓨터만 모든 블록체인을 다운받는 '풀노드(full node)'가 될 수 있는데 이 머클트리의 이진트리 방식은 우리가 가지고 다니는 모바일로도 블록데이터의 일부만 다운받는 '라이트 노드(light node)'로서 쉽고 빠르게 특정 거래를 찾도록 해준다.
이것이 머클트리가 블록에서 맡은 역할이다.
최대한 쉽게 설명하려고 하지만 모르시는 분들을 위해 언제든지 댓글로 질문을 받습니다.
질문의 내용이 길 경우는 jsralphh@gmail.com으로 보내주시면 감사하겠습니다.
너무 도움이 되는 글이라 리스팀합니다~
네 감사합니다~ 자주들려주세요!
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://steemit.com/kr/@jsralph/merkle-trees
이전 계정 https://steemit.com/@jsralph 분실하여 새로 계정을 만들게 되었습니다.
블록체인 관련 포스팅들 이곳에 계속 올라옵니다~
안녕하세요! 글 너무 잘 보고 있습니다~ 뒤늦게 관심 가지고 공부하고 있는데 문송하는중이네요 계속... 혹시 공부는 어떻게 이렇게 까지 하셨나요? 혹시 스터디 같은거 하세요?
서적을 찾거나 트위터나 백서를 읽습니다~
영어가 되신다면 백서를 추천드립니다