Training & Test data

지금까지 우리는 우리 손에 가지고 있는 x_data와 y_data를 모두 사용해서 학습을 진행했다. 하지만 실제로 학습을 진행할 때 이런 방법은 독약과 같다. Overfitting, 즉 샘플 데이터에 너무나 최적화된 학습을 진행할 위험이 발생하기 때문이다. 우리 손에 가지고 있는 데이터에는 너무나도 잘 맞아떨어지지만, 새로운 임의의 데이터를 가지고 예측을 시도할 때 엉뚱한 값이 도출될 수 있다. 완벽하게 틀리는 것보다 대략적으로 맞는 것이 낫다

Overfitting 문제를 해결하기 위해 우리는 손에 들고 있는 모든 데이터를 모두 한 번에 학습시키지 않는다. x_data 중 일부를 train_data와 test_data로 나누어 우리가 가지고 있는 데이터로 우리가 가지고 있는 결과값을 예측해 그 정확도를 높여가는 방법을 사용한다.

x_data = [[1, 2, 1], [1, 3, 2], [1, 3, 4], [1, 5, 5], [1, 7, 5], [1, 2, 5], [1, 6, 6], [1, 7, 7]]
y_data = [[0, 0, 1], [0, 0, 1], [0, 0, 1],[0, 1, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [1, 0, 0]]

# Evaluation our model using this test dataset
x_test = [[2, 1, 1], [3, 1, 2], [3, 3, 4]]
y_test = [[0, 0, 1], [0, 0, 1], [0, 0, 1]]

이렇게 X와 Y 모두 train_data와 test_data로 나눠볼 수 있다. x_data와 y_data를 학습시킨 후, x_test로 y_test를 예측할 것이다.

import tensorflow as tf

X = tf.placeholder('float', [None, 3])
Y = tf.placeholder('float', [None, 3])
W = tf.Variable(tf.random_normal([3, 3]))
b = tf.Variable(tf.random_normal([3]))

hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis = 1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)

# Correct prediction Test model
prediction = tf.argmax(hypothesis, 1)
is_correct = tf.equal(prediction, tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))

그동안 우리가 배워온 내용을 그대로 옮겼다. 한정된 숫자의 결과물을 예측하는 학습이기 때문에 softmax classifier를 사용하고 예측값과 실제 결과값이 얼마나 일치하는지 accuracy도 계산한다.

# Launch graph
with tf.Session() as sess:
    # Initialize TensorFlow variables
    sess.run(tf.global_variables_initializer())
    for step in range(201):
        cost_val, W_val, _ = sess.run([cost, W, optimizer], feed_dict={X: x_data, Y: y_data})
        if step % 50 == 0:
            print(step, cost_val, W_val)
        
    # predict
    print('Prediction: ', sess.run(prediction, feed_dict={X: x_test}))
    #Calculate the accuracy
    print('Accuracy: ', sess.run(accuracy, feed_dict={X: x_test, Y: y_test}))

마찬가지로 그동안 우리가 새로운 데이터를 받아 예측값을 도출해냈던 과정과 같다. 다만 이제는 새로운 데이터가 아니라 우리 손에 가지고 있었던 x_test를 feed_dict에 넣어 결과값과 비교할 것이다.

0 8.988228 [[ 0.11208847  0.47554475  0.1975143 ]
 [-1.1675632   1.5306576   0.5912204 ]
 [ 0.09794842  0.1834646  -1.4173911 ]]
50 0.67657614 [[-0.14361657  0.31683704  0.6119269 ]
 [ 0.18957865  0.28083315  0.4839031 ]
 [ 0.20006129 -0.22995412 -1.106085  ]]
100 0.6029661 [[-0.38646892  0.28959692  0.8820194 ]
 [ 0.38143796  0.252741    0.32013616]
 [ 0.1023661  -0.18497579 -1.0533681 ]]
150 0.56602275 [[-0.584517    0.27159134  1.098073  ]
 [ 0.43722993  0.27073687  0.24634846]
 [ 0.12417976 -0.18668653 -1.0734707 ]]
200 0.5386059 [[-0.76213515  0.2664096   1.2808731 ]
 [ 0.45737296  0.2853071   0.21163537]
 [ 0.1737314  -0.19095026 -1.1187582 ]]
Prediction:  [2 2 2]
Accuracy:  1.0

결과적으로 accuracy가 1.0으로 완벽하게 맞아떨어졌다. 우리 데이터 중 일부만 가지고서도 효과적인 학습이 이루어졌다는 의미다.

Learning Rate

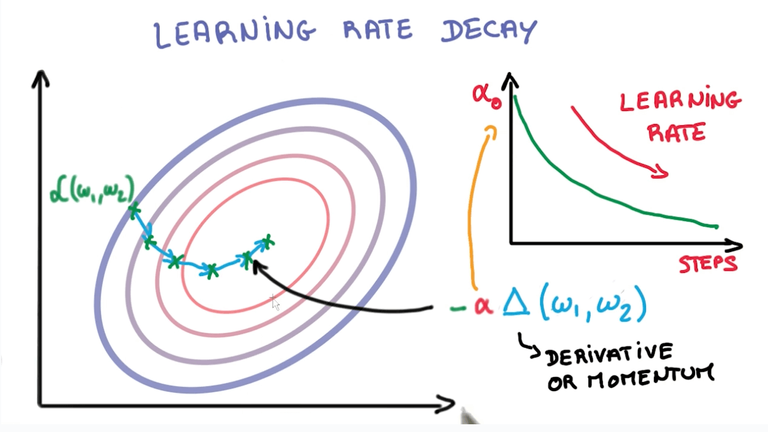
앞서 배웠던 수식 중 위 그림에서 표현되는 α가 learning_rate을 의미함을 배웠다. 거의 대부분의 상황에서 양 극단은 좋지 않은 결과를 가져온다. learning_rate 역시 마찬가지다.

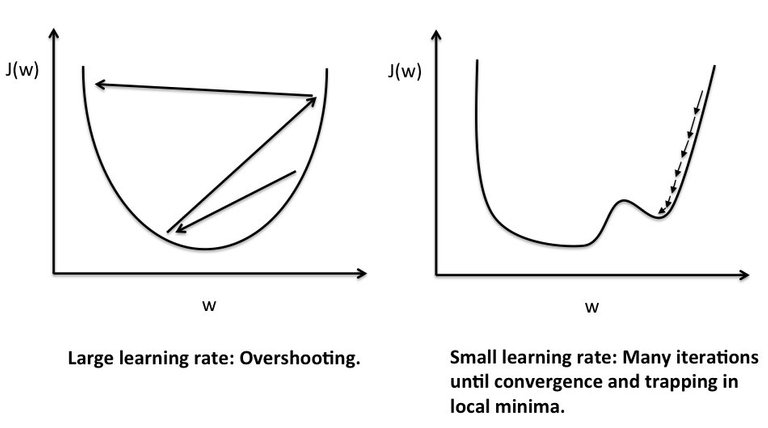
왼쪽 그림은 learning_rate가 너무 큰 값을 경우 발생하는 overshooting을 표현한 그림이다. cost의 최저 지점을 찾아기기 위해 학습을 진행하려하지만 learning_rate가 너무 큰 바람에 그래프를 이리저리 튕겨다니다가 결국 그래프 밖으로 나가버린다.

반대로 오른쪽 그림은 learning_rate가 너무 낮은 경우다. local minumum이라고 부르는 계곡에 갇혀버렸다. 이곳이 정말 모든 cost의 최저점인줄 알고 학습을 멈출 수 있는 위험이 발생한 상황이다. 이렇듯 learning_rate는 너무 높거나 낮은 경우 모두 학습에 문제를 발생시킨다.

X = tf.placeholder('float', [None, 3])
Y = tf.placeholder('float', [None, 3])
W = tf.Variable(tf.random_normal([3, 3]))
b = tf.Variable(tf.random_normal([3]))

hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis = 1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1.5).minimize(cost)

# Correct prediction Test model
prediction = tf.argmax(hypothesis, 1)
is_correct = tf.equal(prediction, tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))

# Launch graph
with tf.Session() as sess:
    # Initialize TensorFlow variables
    sess.run(tf.global_variables_initializer())
    for step in range(201):
        cost_val, W_val, _ = sess.run([cost, W, optimizer], feed_dict={X: x_data, Y: y_data})
        if step % 50 == 0:
            print(step, cost_val, W_val)
        
    # predict
    print('Prediction: ', sess.run(prediction, feed_dict={X: x_test}))
    #Calculate the accuracy
    print('Accuracy: ', sess.run(accuracy, feed_dict={X: x_test, Y: y_test}))

위 코드는 learning_rate = 1.5인 경우다. 너무 높은 수치가 도입될 경우 어떤 문제가 발생하는지 알아보자.

0 8.564701 [[ 0.00467372 -1.7712536   0.44246456]
 [ 0.5064486  -2.9807346   1.3701193 ]
 [ 0.64034474 -1.9685894   0.32826614]]
50 nan [[nan nan nan]
 [nan nan nan]
 [nan nan nan]]
100 nan [[nan nan nan]
 [nan nan nan]
 [nan nan nan]]
150 nan [[nan nan nan]
 [nan nan nan]
 [nan nan nan]]
200 nan [[nan nan nan]
 [nan nan nan]
 [nan nan nan]]
Prediction:  [0 0 0]
Accuracy:  0.0

아예 NaN 값으로 표시되며 학습을 전혀 진행하지 못한다. 학습을 하다가 그래프 밖으로 튕겨져 나갔기 때문이다. 반대로 learning_rate가 낮은 경우도 살펴보자.

X = tf.placeholder('float', [None, 3])
Y = tf.placeholder('float', [None, 3])
W = tf.Variable(tf.random_normal([3, 3]))
b = tf.Variable(tf.random_normal([3]))

hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis = 1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-10).minimize(cost)

# Correct prediction Test model
prediction = tf.argmax(hypothesis, 1)
is_correct = tf.equal(prediction, tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))

# Launch graph
with tf.Session() as sess:
    # Initialize TensorFlow variables
    sess.run(tf.global_variables_initializer())
    for step in range(201):
        cost_val, W_val, _ = sess.run([cost, W, optimizer], feed_dict={X: x_data, Y: y_data})
        if step % 50 == 0:
            print(step, cost_val, W_val)
        
    # predict
    print('Prediction: ', sess.run(prediction, feed_dict={X: x_test}))
    #Calculate the accuracy
    print('Accuracy: ', sess.run(accuracy, feed_dict={X: x_test, Y: y_test}))

learning_rate=1e-10이라는 작은 수를 넣은 것 빼고는 모두다 같은 코드다. 결과는 아래와 같다.

0 14.259041 [[-0.2004612  -0.09101935 -1.281261  ]
 [ 1.9522957  -2.5888934   1.4537743 ]
 [ 0.5717957  -1.5132546   1.8434129 ]]
50 14.259041 [[-0.2004612  -0.09101935 -1.281261  ]
 [ 1.9522957  -2.5888934   1.4537743 ]
 [ 0.5717957  -1.5132546   1.8434129 ]]
100 14.259041 [[-0.2004612  -0.09101935 -1.281261  ]
 [ 1.9522957  -2.5888934   1.4537743 ]
 [ 0.5717957  -1.5132546   1.8434129 ]]
150 14.259041 [[-0.2004612  -0.09101935 -1.281261  ]
 [ 1.9522957  -2.5888934   1.4537743 ]
 [ 0.5717957  -1.5132546   1.8434129 ]]
200 14.259041 [[-0.2004612  -0.09101935 -1.281261  ]
 [ 1.9522957  -2.5888934   1.4537743 ]
 [ 0.5717957  -1.5132546   1.8434129 ]]
Prediction:  [0 0 2]
Accuracy:  0.33333334

accuracy가 0.3333으로 낮은 것을 확인할 수 있다. 너무 학습 진도가 느려서 200 번의 회차 안에 cost의 최저점에 도달하지 못했거나 local minimum에 도달해 학습을 멈춰버린 결과일 수 있다. cost 수치가 14.259041이라는 특정 수치에 머물러 있는 것을 보면 후자의 경우라고 추측해볼 수 있다.

Non-normalized Input

import numpy as np

xy = np.array([[828.659973, 833.450012, 908100, 828.349976, 831.659973],
               [823.02002, 828.070007, 1828100, 821.655029, 828.070007],
               [819.929993, 824.400024, 1438100, 818.97998, 824.159973],
               [816, 820.958984, 1008100, 815.48999, 819.23999],
               [819.359985, 823, 1188100, 818.469971, 818.97998],
               [819, 823, 1198100, 816, 820.450012],
               [811.700012, 815.25, 1098100, 809.780029, 813.669983],
               [809.51001, 816.659973, 1398100, 804.539978, 809.559998]])

위와 같이 복잡한 숫자를 다뤄야 할 경우가 있다. 하지만 TensorFlow로 학습을 시키면 학습이 잘 이뤄지지 않는다. 그림으로 살펴보자.

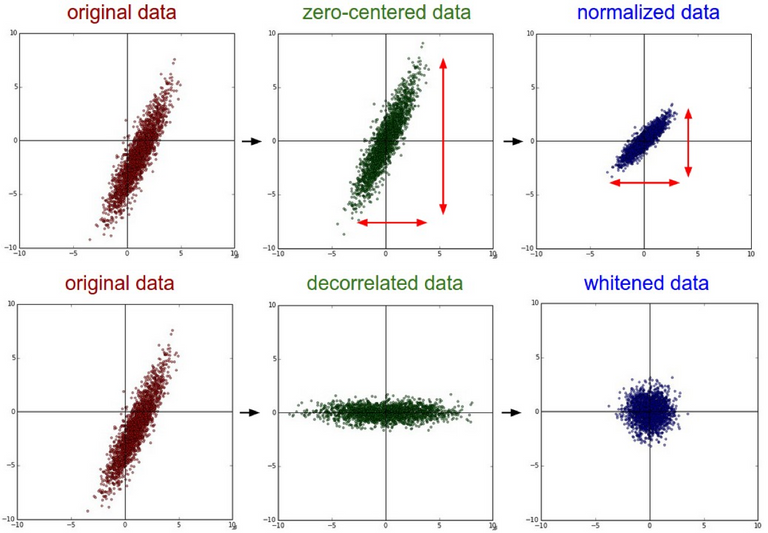
현재 가장 왼쪽에 있는 그림이 위 데이터를 나타난 그래프다. 이런 상태 그래도 학습을 진행하면 학습을 하다가 learning_rate이 클 경우와 비슷하게 그래프 밖으로 튕겨져 나가버린다. 데이터의 형태가 일정하지 않기 때문이다. 이를 위해 우리는 가장 오른쪽의 그림으로 데이터를 변형시켜줘야 한다. 이를 nomalization 즉, 정규화라고 한다.

x_data = xy[:, 0:-1]
y_data = xy[: ,[-1]]

# Placeholders for a tensor that will be always fed
X = tf.placeholder(tf.float32, shape=[None, 4])
Y = tf.placeholder(tf.float32, shape=[None, 1])
W = tf.Variable(tf.random_normal([4, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

hypothesis = tf.matmul(X, W) + b
cost = tf.reduce_mean(tf.square(hypothesis - Y))

# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)
train = optimizer.minimize(cost)

sess = tf.Session()
sess.run(tf.global_variables_initializer())
for step in range(2001):
    cost_val, hy_val, _ = sess.run([cost, hypothesis, train], feed_dict={X: x_data, Y: y_data})
    if step%500 == 0:
        print(step, 'Cost: ', cost_val, '\nPrediction:\n', hy_val)

먼저 정규화 과정 이전의 데이터 그대로 학습을 진행해보자. 지금껏 우리가 배운 내용 그대로의 linear regression 코드다.

0 Cost:  5284707300.0 
Prediction:
 [[ -50129.914]
 [-102780.71 ]
 [ -80473.99 ]
 [ -55879.113]
 [ -66172.24 ]
 [ -66744.15 ]
 [ -61039.453]
 [ -78203.71 ]]
...
2000 Cost:  nan 
Prediction:
 [[nan]
 [nan]
 [nan]
 [nan]
 [nan]
 [nan]
 [nan]
 [nan]]

역시나 우리의 예상대로 NaN 값이 나오면서 학습이 이루어지지 않았다. 그래프 밖으로 학습 곡선이 튕겨져 나갔기 때문이다. 이제 Normalization을 해보자.

def MinMaxScaler(data):
    numerator = data - np.min(data, 0)
    denominator = np.max(data, 0) - np.min(data, 0)
    # noise term prevents the zero division
    return numerator / (denominator + 1e-7)
    
xy = MinMaxScaler(xy)
print(xy)

Normalization을 해주는 MinMaxScaler 함수를 만들어 xy에 적용한다.

[[0.99999999 0.99999999 0.         1.         1.        ]
 [0.70548491 0.70439552 1.         0.71881782 0.83755791]
 [0.54412549 0.50274824 0.57608696 0.606468   0.6606331 ]
 [0.33890353 0.31368023 0.10869565 0.45989134 0.43800918]
 [0.51436    0.42582389 0.30434783 0.58504805 0.42624401]
 [0.49556179 0.42582389 0.31521739 0.48131134 0.49276137]
 [0.11436064 0.         0.20652174 0.22007776 0.18597238]
 [0.         0.07747099 0.5326087  0.         0.        ]]

앞서 여러 복잡한 숫자로 이뤄진 데이터 값들이 0 ~ 1까지의 값으로 정리되었다. 이제 학습을 진행할 수 있는 상태가 된 것이다.

x_data = xy[:, 0:-1]
y_data = xy[: ,[-1]]

# Placeholders for a tensor that will be always fed
X = tf.placeholder(tf.float32, shape=[None, 4])
Y = tf.placeholder(tf.float32, shape=[None, 1])
W = tf.Variable(tf.random_normal([4, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

hypothesis = tf.matmul(X, W) + b
cost = tf.reduce_mean(tf.square(hypothesis - Y))

# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)
train = optimizer.minimize(cost)

sess = tf.Session()
sess.run(tf.global_variables_initializer())
for step in range(2001):
    cost_val, hy_val, _ = sess.run([cost, hypothesis, train], feed_dict={X: x_data, Y: y_data})
    if step%500 == 0:
        print(step, 'Cost: ', cost_val, '\nPrediction:\n', hy_val)

다시 linear regression 코드를 돌려보면,

0 Cost:  0.231175 
Prediction:
 [[0.20675151]
 [0.07358359]
 [0.0928963 ]
 [0.08791228]
 [0.13289304]
 [0.18657236]
 [0.11113021]
 [0.07873628]]
500 Cost:  0.0050764065 
Prediction:
 [[1.0107089 ]
 [0.80649084]
 [0.59782326]
 [0.3328081 ]
 [0.5462328 ]
 [0.55248463]
 [0.1339626 ]
 [0.06204735]]
1000 Cost:  0.0046706144 
Prediction:
 [[1.0036284 ]
 [0.8089594 ]
 [0.6028423 ]
 [0.33763686]
 [0.5518892 ]
 [0.54710376]
 [0.14128152]
 [0.04881008]]
1500 Cost:  0.0044109067 
Prediction:
 [[0.9986937 ]
 [0.810721  ]
 [0.6065419 ]
 [0.34182253]
 [0.5557763 ]
 [0.5424629 ]
 [0.14631456]
 [0.03957276]]
2000 Cost:  0.004228479 
Prediction:
 [[0.9952446 ]
 [0.8120657 ]
 [0.60932547]
 [0.34547907]
 [0.55840313]
 [0.5383644 ]
 [0.14969271]
 [0.03315411]]

cost가 줄어들며 학습이 잘 진행되고 있는 것을 확인할 수 있다. 큰 범위의 데이터 학습을 진행할 경우 정규화 과정을 거쳐야 학습이 진행될 수 있다.

Sort:

Trending

[-]

steemitboard (66) 7 years ago

Congratulations @beseeyong! You have completed some achievement on Steemit and have been rewarded with new badge(s) :

Award for the number of upvotes

Click on any badge to view your own Board of Honor on SteemitBoard.

To support your work, I also upvoted your post!
For more information about SteemitBoard, click here

If you no longer want to receive notifications, reply to this comment with the word STOP

Upvote this notification to help all Steemit users. Learn why here!

$0.00

virus707 (76) 7 years ago

5월 다시 파이팅해요!
호출에 감사드립니다!

pairplay (67) 7 years ago

pairplay 가 kr-dev 컨텐츠를 응원합니다! :)

[머신러닝] Traing/Test, Learning Rate와 Normalization으로 학습 효과 높이기

Training & Test data

Learning Rate

Non-normalized Input