살아가면서 황금비의 이야기를 많이 들었지만, 백금(은)비 이야기는 별로 들은 적이 없었다.
사쿠라이 스스무가 쓴 "일상생활 속에 숨어있는 수학" 을 읽는 도중 백은비 이야기가 나왔다.
저자 자신이 일본인이라 그런지 일본 문화에서 등장하는 백은비에 대해 많이 강조한다.
일례로 황금비[숫자로 이야기 하면 8:5의 비율, 흔히 말하는 8등신 비율이 이 황금비율과 관련이 있다.] 는 자연에서 발견된 서양의 아름다움을 상징한다고 말하고, 백은비[숫자로 이야기하면 7:5, 굳이 말하자면 이 비율은 7등신 비율이라고 할 수 있겠다. ]는 인위적인 아름다움을 이야기 하며 일본의 아름다움을 상징한다고 서술했다.
그리고 대표적 예시로 일본의 다다미라던지, 일본의 꽃꽃이[7:5:3] 등을 예시로 들었다. [일본에서 정사각형을 기준으로 한 건물들에 이런 비율이 자주 등장한다고 한다.] 사실 일본을 넘어서서 A4 용지가 이 비율을 가지고 있다.
굳이 일본에 국한하지 않고, 이 백은비를 동양 전반적으로 확장 할 수 있다. [참고로 이 백은비는 다른 말로는 백금비, 혹은 금강비율이라고도 한다.]
일단 이 황금비와 금강비율을 비교해 보자. 저자가 말한대로 금강비율의 경우는 정사각형으로부터, 황금비율의 경우 정오각형으로 부터 구할 수 있다.
이 수의 비율이 앞에 말한 그 비율이다. 간단히 비율을 풀어 쓰면 이를 보일 수 있다.
황금비는 영어표현이 Golden ratio 고 한문도 황금비이지만, 금강비는 영어 표현이 닮음비이다. ㅋㅋㅋ[ ratio of similarity ] 참고로 위키피디아에 적혀있는 백은비는 1 : 1 + \sqrt{2} 라고 한다. [이 때의 영어 표현은 silver ratio 이다.] 뭐 용어에 대해서는 아직 통일이 되어 있지 않은 듯 싶다. 황금비는 동서양 모두 유명하지만 금강비니, 백은비는 비교적 서구권에 유명하지 않아서 그런가?
책에서 일본의 금강비에 대해 예를 들었는데, 우리나라에도 이 금강비의 예제들이 있다.
첨성대의 밑단의 지름과 곡면의 상한 기둥까지의 높이의 비가 이 백금비이며, 포석정의 가로 세로의 비율, 무량수전, 석굴암 등 우리나라의 건축물에서도 이 비율이 등장한다.
사실 개인적으로 이런 비율은 충분히 짜맞출수 있다고도 본다.
첨성대의 경우, 황금 비율로도 볼 수 있고, 또 금강비율로도 볼 수 있다. 해당 비율로 잡을 것을 무엇으로 하느냐에 따라 이 비율을 "조정"가능하다.
ㅋㅋㅋㅋㅋ 동양의 대표 미인이라고 불리는 양귀비와 서양의 대표 미인이라고 불리는 클레오파트라 [근데 사실 클레오파트라는 이집트니까 서양보다는 아프리카나 서아시아 쪽이 아닌가? 이스라엘, 팔레스타인, 이 쪽이 다 중동, 서아시아 아닌가....]
양귀비 초상화의 이마에서 미간까지와 미간에서 턱까지의 비율, 콧등에서 턱까지의 비율이 모두 1:1.4 라고 클레오파트라는 코와 눈썹을 기준으로 1:1.68 비율 이라고 한다.
ㅋㅋㅋㅋㅋㅋ
진짜 이런거 비율 찾아내는 것도 쉽지 않아 보인다.
여담 1 유클리드의 황금비 정의
유클리드는 황금비를 다음과 같이 정의했다.
어떤 직선에서 그 전체 직선과 그 일부 큰 선분의 길이의 비가 큰 선분의 길이와 그 작은 선분의 길이의 비와 같을 때, 그 길이가 황금비로 잘려진다고 말한다.
이 중 양수인 (1+\sqrt{5})/2 가 우리가 말하는 황금비율로 자른 길이가 된다.
일단 이 수는 무리수이다. [유리수+무리수=무리수이다.] 이 수는 신성한 수라고도 불리는데 그 이유는 이 식의 연분비 표현식에 있다.
저 연분비가 진짜 황금비랑 같은 수가 된다는 것은 수식 표현의 닮음 구조에서 쉽게 읽어낼 수 있다.
여담 2 cos 36도 구하기
여담으로 cos(36도) 가 어떻게 저 값을 가지는지 한번 증명해 보자. [사실 이는 예전 고등학교 삼각함수 교과과정으로도 구할 수 있는 내용이다. 삼각함수의 덧셈 공식들과 2차 방정식을 풀어야 한다. ]
먼저 삼각함수 공식을 살펴보자
자 이를 풀면





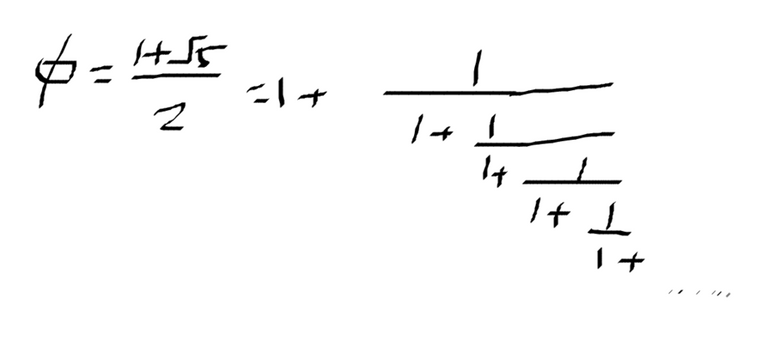

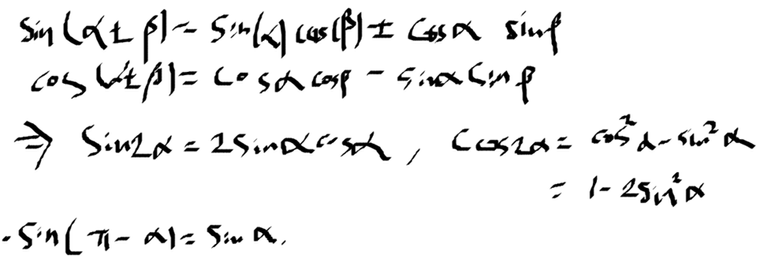


온갖 비율이 다 있네요~ beoped님도 beoped 비를 한번 만들어봐요~!! ㅋㅋ
Posted using Partiko Android
ㅋㅋㅋㅋㅋㅋ