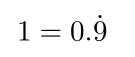
오늘 다루려고 하는 주제는 1=0.9땡 의 의미를 살펴 보는 것이다.
중학교 수학 내용인데 사실 고등학교 때 배운 무한등비급수의 개념을 잘 알고 있다면 크게 혼란이 오지 않는 내용이다.
하지만 중학교 친구들은 무한급수의 합을 배우지 않은 상태.. 일단 무한등비급수의 합을 알고 있다고 생각하고 0.9 땡을 전개해보자
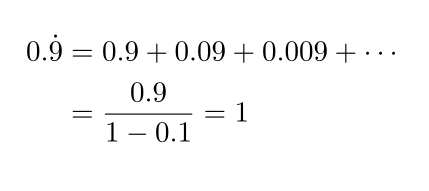
이 식의 가장 강력한 점은 0.9 땡이 정확히 1이라는 것이다.
왜 정확히냐, 몇몇 사람들은 0.9 땡은 1보다 작지 않냐고 주장하기도 하는데, 이는 0.9땡의 정의를 제대로 이해하지 못해서이다. 0.9 땡은 9가 유한하게 있는게 아니라 무한하게 있는 것이다.
0.9 땡이 1보자 작다고 하면 0.9 땡에 어떤 수를 더해야 1이 될까? 0.9땡의 9가 유한하다면 우리는 1과 상보적인 수, 즉 더해서 1을 만들 수 있는 수를 생각할 수 있다. 대표적으로 0.9 경우 0.1 이 있을 것이고 0.99 의 경우 0.01 이 있을 것이다. 자 이제 0.9 땡으로 가보자 0.9 땡의 9는 무한하게 유지된다. 이 값이 1보다 작다면, 0.0... 1 이 있다는 것인데 0의 무한대 갯수와 9의 무한대 갯수가 한개이상 차이가 나야 된다. 정수의 무한대 갯수를 구별하는것은 의미가 없는 일이기에 결국 그 상보적인 수는 0.000이 무한개 있는 수 0이 되어버린다.
순환소수는 이런 의미에서 매우 재미있는 수이다.
사실 중학교 교육과정에서
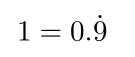
를 보이기 위해선 일단 0.1땡의 정의를 알아야 하는데 여기선 아예 시작부터 0.1 땡을 1/9로 정의한다. [사실 1을 9로 나누면서 이 순환소수 챕터를 시작한다...]
이렇게 시작하면, 쿤 문제 없이 다른 순환소수들을 쉽게 계산할 수 있다.
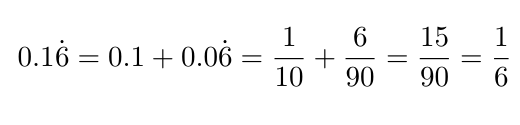
[ 하지만 순환마디가 생기면 어떨까? 이것도 사실 규칙성이 있다. 1/7 만 해도 142857 이 반복된다. ]
이 순환소수 부분이 중학교 수학에 중요한 이유는 (얼핏 보면 굳이 순환소수는 어떤 분수형태니 굳이 중학교 때 배울 필요가 있냐라고 생각하기 쉽다. 순환소수의 계산은 결국엔 순환소수에 해당하는 분수형태를 찾아 계산하는 것이니까 말이다) 바로 이 순환소수는 무한한 숫자의 합이 유한하다는 것을 알려주는 가장 직관적인 예이기 때문이다.
순환소수는 소수로 표현하면 무한히 많이 적히지만 사실은 유한한 값이다. 여담으로 순환소수의 순환마디에 따른 형태에 대해 OEIS 의 수열에서 검색할 수 있다. ( 관련 글-[수학] OEIS
우리는 무한에 대해 종종 환상을 가지고 있다. 직관적으로 어떤 것을 무한히 더하면 무한대가 될 것이라는 생각이 쉽게 든다. 무한대의 진정한 재미는 이러한 직관이 깨진다는 것이다. 순환소수는 아마 교육과정에서 처음 등장하는 무한등비급수 예제가 아닌가 싶다.
지나가던 문과 출신이라 납득이 어렵습니다. /// 0.9땡에 더해서 1이되는 수가 0.00000 무한히 이어진다.... 까지는 이해했는데 // 0.000000 무한히 이어지는게 왜 0이 되는지는 납득이 어렵습니다. /// 전자는 무한히 줄어들 뿐 무언가다 있는 것이고.. 후자는 전적으로 없는 것이고 단위로 딱 끊어지는 것 아닌지요. // 0.9땡도 무한히 1에 가까워지는 것이지, 완전히 1이라는 단위로 끊어지는 그 경계선에 닿지는 못하는 것 처럼 보입니다.
혹시 보다 쉽게 친절히 쉽게 설명해주실 수 있으십니까?
이 문제의 핵심은 무한에 있습니다.
무한히 이어진다는 것, 무한이 더한다는 것 때문에 흔히 무한이 더한 값은 무한한 값을 가질 것이라는 생각을 쉽게 하곤 합니다.
무한한 항을 더했을 때 유한한 값을 가질 수 있다는 것, 이것이 무한급수의 묘미이자 매력입니다. 이 글에서 순환소수는 무한급수의 한 예로써 십진법으로 소수로 표현했을 때 무한하게 적히지만 그 값이 유한합니다. (분수꼴로 쓸 수 있다는 것을 말하죠)
[즉 10진법으로 표현할 때 어떤 값들의 무한한 합으로 표현된다는 것입니다.
0.1234 = 1*10^{-1} + 2 * 10^{-2} + ... 처럼, 소수 이하 자리들을 이런 식으로 합으로 표현할 수 있으니까요 ]
0.9땡은 생김새 때문에 무한히 1에 가까워 진다고 여겨지나 무한히 1에 가까워 지는게 아니라 정확히 1이라는 것이 이 포스팅에서 말하고 싶은 것이었습니다.
0.9 땡의 소숫점이 유한하게 표현된다면 0.9 땡에 1이 되는 숫자를 유한하게 표현할 수 있지만, 0.9 땡의 소숫점이 무한하다면 0.9 땡에 1이 되는 숫자를 무한+1 번째에 1이 있는 숫자로 쓸 수 없다는 것을 이야기 하고 싶은 거였습니다. (무한+1)= 무한이 되어버리니까요
사실 이 말을 쓴 것은 직관적으로 0.9 땡이 1이 된다는 것을 보이고 싶어서 넣은 구절인데, 지금 보니까 오해의 소지가 있어 보이는군요 ㅎㅎ;
아.... 댓글쓰다가 깨닳아버렷다.
0.1111 무한히 이어짐은 1/9
0.2222 무한히 이어짐은 2/9
0.3333 무한히 이어짐은 3/9
.
.
0.8888 무한히 이어짐은 8/9
0.9999 무한히 이어짐은 9/9
그런데
9로 9를 나누는데 바로 1 도출 안하고
9로 9.0를 나누면서
일부러 위에 0.9 올리고
아래에 8.1 내려줬더니
나머지로 0.9가 냐오네요.
그럼 이걸 무한히 반복할 수 있다.
그래서 9/9다......
그럼 애초에 0.999999 무한히 이어짐은, 일부러 수학의 원리를 파들어가기 위해 저렇게 계산해서 내려가지 않는
한 볼 일 없는 수 인 건가요?
ㅋㅋㅋ 그렇죠
사실 10진법에 기반을 두고 있어서 이런 순환소수들이 무서워(?) 보이는 건데, 분수 형태를 쓰거나 다른 진법으로 가면 유한하게 끊어 표현할 수 있습니다 ㅎㅎ
제가 수학교육학과를 나온게 아니어서 왜 순환소수 내용이 중학교 주제로 선정되었는지 정확히는 알 수 없지만, 제 나름으로 고등학교 때 배울 무한급수를 위해 무한에 대해서 노출하기 위해서 낸게 아닌가 생각해 봤습니다 ㅎㅎ
적콩무에서 무한대의 크기가 비교가 가능하단걸 들었(?) 배워씁니다. 공대 테크에 수학을 좋아하는 축에 속한다고 했던 저로서도 쇼킹하더군요. 이공수학과 순수(?)수학은 또 차이가 나는 듯 하네요. 이 순환소수도 개념은 알았지만 이렇게 설명해주시니 완전 새롭네요. 잘 베웠습니다.
무한대의 크기 비교는 일대일 대응 함수를 만들어서 표현할 수 있지요! ㅎㅎ
인터넷에서 심심하면 나오는 떡밥 0.9가 왜 1인가요? ㅎㅎㅎㅎ
무한한 것이 어디론가 '수렴'한다는데에서 마음의 평화가 찾아옵니다.