🔸 English version

How can the math of ‘I don’t know if…’ help improve the Democratic Deliberative Process?

By Dr. Ranulfo Paiva Sobrinho & M.A. Karla Córdoba-Brenes

(Created using DeepAI)

A Democratic Deliberative Process entails the exchange of ideas and arguments among individuals, aiming to reach practices and decisions that are not influenced by personal interests or biases, but rather reflect the greater good and common interests of the public. This process has the potential to generate legitimate and consensus-based decisions made by citizens. Furthermore, it promotes civic engagement and education by providing opportunities for citizens to learn from one another and from experts, fostering the development of civic skills and attitudes. Ultimately, it plays a significant role in the establishment and reinforcement of Open Democracy [1].
.

Fortunately, there are initiatives aimed at implementing the Democratic Deliberative Process on a global scale, making it accessible to a wider range of citizens.

.

One notable example is Pol.is [2], an innovative platform that facilitates the real-time collection, analysis, and comprehension of the thoughts and opinions of large groups of people. This system utilizes advanced statistics and machine learning techniques to enable individuals to express their views in their own words.

However, it is important to acknowledge that the Democratic Deliberative Process is not without its challenges. One aspect that often goes unnoticed is the mathematical limitations inherent in traditional deliberative processes. Our decision-making processes in politics, business, and even on a personal level are heavily influenced by Boolean mathematics, which revolves around binary choices of “Yes” and “No” or opposing poles. While this simplification can be helpful, it also leads to a loss of valuable information and the inability to express opinions as a nuanced spectrum.
.

Boolean mathematics forces us to choose a single option, even when our stance on complex issues may not align entirely with either extreme of “Yes” or “No.”

.

Another challenge lies in ensuring the diversity and representativeness of deliberators, particularly when marginalized groups are excluded from public discourse, and when information and data availability is insufficient or inadequately communicated. These factors pose difficulties for citizens in forming clear opinions about the object under analysis.

Usually, in this context, people could say “I don’t know if I understand, or, if I don’t understand”, or* “I don’t know if I agree, or if I don’t agree”, or “I don’t know if I vote, or if I don’t vote”, or “it is not clear enough, I need more information”.* These expressions represent indeterminacy, or neutrality.

This could mean the pieces of information given to them were not enough to help them form a judgment to vote or not to vote, or accept or not accept, or take other actions (agree, understand, choose). These people need more information that can help them reduce indeterminacy, or neutrality regarding the object in analysis.
.

A Collective Response System

In the context of a collective response system, it is desirable the system prioritizes supporting/understanding a group and its decision-making over supporting/understanding an individual and their decision-making [3]. How to get inputs from citizens in situations marked by high levels of indeterminacy, and how to process this type of information?

For didactic purposes, let’s suppose that a collective response system is structured in two simple steps. The purpose of this system is to get a set of statements representing the group’s opinion regarding a specific topic.

In step 1, given a specific context, people express their ideas by writing them down in a short statement. Other members can give feedback related to each statement expressing how much they understood it. If necessary, people can ask the proponents to offer more details about the statement. Only those statements that reach an acceptable level of understanding by the group can be eligible to advance to the next step.

In step 2, people vote on which statement represents the opinion of the group.

As an example, given the context where people should deliberate about the evolution of artificial intelligence and its risks regarding human lives, one person could write the following hypothetical statement:
.

“Our society needs to restrict the evolution of artificial intelligence especially when dealing with moral, ethical issues”.

.

Other members of the group are invited to express their opinions regarding the statement. They could respond, I understand, or, I don’t understand, or Skip the statement, choosing not to express their opinion.

This is similar to what Pol.is applied to the following example, a process for people to express their opinion on the topics to be discussed in an alignment assembly. Members are given three options: agree, disagree or skip/undecided.

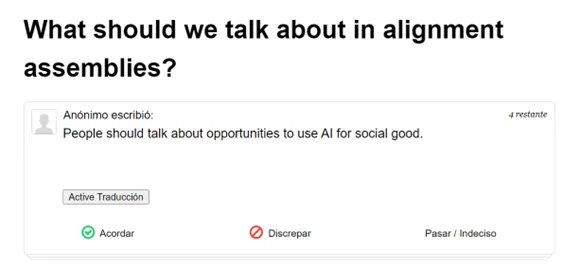
(Source: screenshot taken from https://cip.org/blog/alignment)

These are certainly valuable inputs, but what if each person could express , and, at the same time, <how much it doesn’t know if it understands or not understands>, and ? Wouldn’t that offer a more nuanced picture of their opinions?

Could the math of “I don’t know if …” help in this case? What possible new insights could it bring to light?
.

Neutrosophy

Created in the nineties by Professor Florentin Smarandache, Neutrosophy, here affectionately called “the math of I don’t know if …”, is a branch of Philosophy that studies the origin, nature, and scope of neutralities, as well as their interactions with different ideational spectra, considering a proposition, theory, concept, event, or entity A in relation to its opposite AntiA, and that which is neither A nor antiA, denoted by neutA [4].

.

A Neutrosophic entity embraces three components relating to the degree of truth (T), the degree of indeterminacy (I), and the degree of falseness (F) of a statement.

.

The degree of indeterminacy is independent of the other two. Each Neutrosophic component {T, I, F} can have a numerical value ranging from 0 up to 1, which means that the sum of them lies in a range between 0 and 3. This is a specific type of Neutrosophic set, called, a Single-Valued Neutrosophic Set (SVNS) proposed by [5].

Given the previously mentioned hypothetical statement: “Our society needs to restrict the evolution of artificial intelligence especially when dealing with moral, ethical issues”; other members could give feedback regarding the statement, expressing their degree of understanding (T), the degree to which they don’t know if they understand or do not understand (indeterminacy) (I), and the degree of not understanding (F).

One person could give their feedback as follows:

My degree of understanding regarding the statement is 20%, but there are parts of the sentence that I don’t know if I understand or don’t understand (90%), and there is a part that I don’t understand (34%).

Alternatively, the feedback could be written as:

“My degrees of understanding, indeterminacy, not understanding are respectively, {20%, 90%, 34%}.”

This sentence could be represented as follows:

Person_1: {0.2, 0.9, 0.34}, equivalent to {T, I, F}

If there is one person, 3, or, 500, or, 1 million, or more, we would have something like this:

Person_2: {0.3, 0.7, 0.1}

Person_3: {0.9, 0.1, 0.2}

Person_n: {Tn, In, Fn}

.

Neutrosophy and the Deliberative Democratic Process

In a deliberative democratic process, members participating could previously agree that eligible statements require a degree of indeterminacy lesser than a threshold. For example, for a statement to be eligible in a specific context, its Indeterminacy must be less than 0.4.

The group could determine if there is a percentage (51%, or another number) of members in the group who expressed a degree of indeterminacy greater than 0.4, in this case, the member who proposed the statement should explain it better to help other members to improve their understanding and reduce indeterminacy.

After the new feedback, one potential result could be that the level of indeterminacy is reduced below the threshold and the statement is now eligible. Another potential result is that the level of indeterminacy remains unchanged, or it is reduced but not below the threshold. In this last case, members could proceed to a new round, or simply record the result and continue with the deliberative process.

The members in the group could agree that the statements that could advance to the next stage are those that reach a lower level of indeterminacy. In this example, the next stage could involve voting on which statements better represent the group. Neutrosophic mathematics would also be used.

Considering the same statement 1 “Our society needs to restrict the evolution of artificial intelligence especially when dealing with moral, ethical issues”, people could express their opinion as follows:

.

Statement 1 opinion example — Degree of Agreement (30%), Degree of Indeterminacy (80%), Degree of Disagreement (20%)

.

Let’s suppose that the data in Table 1 represents the opinions of 6 members regarding statement 1. According to Table 1, the degree of agreement is higher than that of disagreement, however, the degree of indeterminacy is high. Four members agree and two do not. But the level of agreement is low, less than 0.3 for members 2, 3 and 5.

This type of information made explicit by Neutrosophy can help people reflect on whether Statement 1 really represents the group.

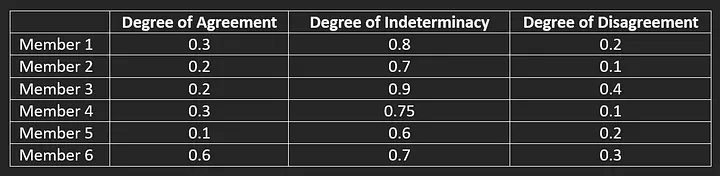
(Table 1 — Opinions of 6 members regarding statement 1 using Neutrosophy)

In this case, the group could have previously agreed that only statements with a lower degree of indeterminacy would represent the group’s opinion. This threshold could be less than 0.45.

They could also agree that more than half plus one of the group members should have a degree of agreement greater than 0.6. So, after a new deliberation, the results are in Table 2.

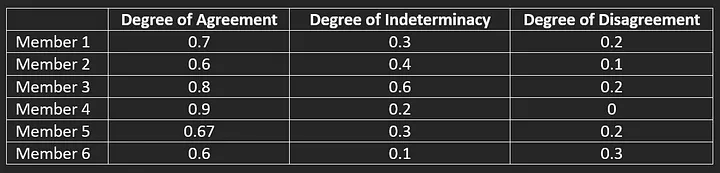
(Table 2 — Opinions of 6 members regarding statement 1 using Neutrosophy. After ‘feedback’)

In this hypothetical case, Table 2 shows that the degree of agreement of most people is now higher than the critical value (0.6), which would imply that sentence 1 could represent the group’s opinion.

These hypothetical situations and data are applicable in real-life scenarios. While we will not delve into specific analytical outcomes in this short non-technical introductory text, it is important to acknowledge their potential significance and relevance in practical contexts.

Neutrosophy includes analysis methods such as Neutrosophic statistics and aggregation methods, among others. In this example, the Neutrosophic set called SNVS was used, which allows applications of Neutrosophy for practical cases. We can explore the application of these metrics in future publications.

.

Reducing Polarized Opinions

Neutrosophy could reduce polarization of ideas by allowing people to express their level of agreement, indeterminacy, and opposition to a specific topic and contribute to a constructive democratic process.

For example, if AI Regulation is being proposed by two political parties, one person could express their opinion as follows:

Person A opinion regarding political party 1 proposal for AI Regulation
I agree with 70%, I have 50% of indeterminacy, I disagree 40%.

Person A opinion regarding political party 2 proposal for AI Regulation
I agree with 60%, I have 40% of indeterminacy, I disagree 30%.

Imagine if instead of one person, we have a group of 1000 people deliberating about the above-mentioned proposals. As person A, each person should express their opinion considering both proposals.

A possible result could be as shown in Table 3.

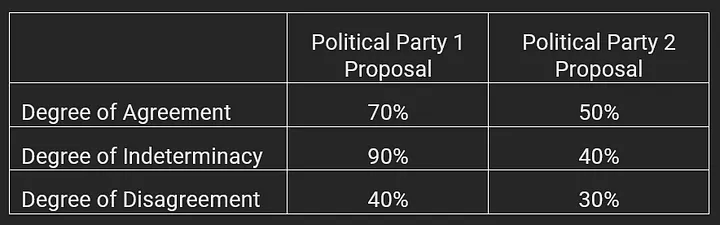
(Table 3 — Opinions of 1000 people about AI Regulation Proposals by Party 1 and Party 2)

In this case, people could request more detailed information from Political Party 1, due to its high level of indeterminacy. If during the deliberative democratic process, people decide that will consider only proposals with a level of indeterminacy lesser than a threshold, for example, 40%, then, according to Table 3 data, they could also request better and clearer information from political party 2.

By adopting this approach, the application of Neutrosophy could play a significant role in mitigating opinion polarization. Neutrosophy encourages individuals to consider both proposals and express their nuanced opinions on the degree of agreement, disagreement, and indeterminacy.

This methodology has the potential to generate improved proposals or statements, particularly in situations characterized by high levels of indeterminacy, where members require more comprehensive information to formulate a final opinion.

.

Conclusions

Democratic deliberative processes are undergoing an evolutionary transformation. Within this evolving landscape, it is crucial to develop methodologies, such as collective intelligence response systems, that embrace more contemporary mathematical frameworks like Neutrosophy.

.

Neutrosophy enables citizens to express their ideas in a manner that transcends binary choices (yes or no), allowing for a more natural and inclusive representation of their inherent ambiguity and indeterminacy. By incorporating such approaches, we can foster a more nuanced and comprehensive democratic discourse.

.

By providing simple examples, individuals can express their opinions while considering varying degrees of agreement, indeterminacy, and disagreement. This approach allows people to transcend opinion polarity and can significantly enhance the democratic deliberation process.

We hope this introductory text can contribute to this process.

.

References

[1] Landemore, H. 2020. Open democracy. Princenton University Press.

[2] https://pol.is/home

[3] Ovadya, A. 2023. ‘Generative CI’ through collective response systems. https://arxiv.org/abs/2302.00672

[4] Smarandache, F. 1999. A unifying field in Logics: Neutrosophic Logic. In Philosophy. American Research Press, 1–141.

[5] Wang, H.; Smarandache, F.; Zhang, Y.; and Sunderraman, R. 2010. Single valued SVNS sets, Multisp Multistruct 4: 410–413.

---

---

🔸 Versão em Português

Como a matemática do 'Eu não sei se...' pode auxiliar a melhorar o Processo Deliberativo Democrático?"

Por Dr. Ranulfo Paiva Sobrinho e M.A. Karla Córdoba-Brenes

(Imagem criada usando DeepAI)

Um Processo Deliberativo Democrático envolve a troca de ideias e argumentos entre indivíduos, com o objetivo de chegar a práticas e decisões que não sejam influenciadas por interesses pessoais ou preconceitos, mas sim reflitam o bem maior e os interesses comuns do público. Esse processo tem o potencial de gerar decisões legítimas e baseadas em consenso feitas pelos cidadãos. Além disso, promove o engajamento cívico e a educação, oferecendo oportunidades para os cidadãos aprenderem uns com os outros e com especialistas, fomentando o desenvolvimento de habilidades e atitudes cívicas. Em última análise, desempenha um papel significativo no estabelecimento e fortalecimento da Democracia Aberta [1].

.

Felizmente, existem iniciativas com o objetivo de implementar o Processo Deliberativo Democrático em escala global, tornando-o acessível a uma ampla gama de cidadãos.

.

Um exemplo notável é o Pol.is [2], uma plataforma inovadora que facilita a coleta, análise e compreensão em tempo real dos pensamentos e opiniões de grandes grupos de pessoas. Esse sistema utiliza técnicas avançadas de estatística e aprendizado de máquina para permitir que os indivíduos expressem suas opiniões com suas próprias palavras.

No entanto, é importante reconhecer que o Processo Deliberativo Democrático não está isento de desafios. Um aspecto que muitas vezes passa despercebido são as limitações matemáticas inerentes aos processos deliberativos tradicionais. Nossos processos de tomada de decisão na política, nos negócios e até mesmo em nível pessoal são fortemente influenciados pela matemática booleana, que gira em torno de escolhas binárias de "Sim" e "Não" ou polos opostos. Embora essa simplificação possa ser útil, ela também leva à perda de informações valiosas e à incapacidade de expressar opiniões como um espectro sutil.

.

A matemática booleana nos força a escolher uma única opção, mesmo quando nossa posição em questões complexas pode não se alinhar completamente com nenhum dos extremos de "Sim" ou "Não".

.

Outro desafio reside em garantir a diversidade e representatividade dos deliberadores, especialmente quando grupos marginalizados são excluídos do discurso público e quando a disponibilidade de informações e dados é insuficiente ou inadequadamente comunicada. Esses fatores representam dificuldades para os cidadãos em formar opiniões claras sobre o objeto em análise.

Geralmente, nesse contexto, as pessoas poderiam dizer "Eu não sei se entendo, ou, se não entendo", ou "Eu não sei se concordo, ou se não concordo", ou "Eu não sei se voto, ou se não voto", ou "não está claro o suficiente, preciso de mais informações". Essas expressões representam indeterminação, ou neutralidade.

Isso poderia significar que as informações fornecidas a eles não foram suficientes para ajudá-los a formar um julgamento para votar ou não votar, ou aceitar ou não aceitar, ou tomar outras ações (concordar, entender, escolher). Essas pessoas precisam de mais informações que possam ajudá-las a reduzir a indeterminação ou a neutralidade em relação ao objeto em análise.

.

Um Sistema de Resposta Coletiva

No contexto de um sistema de resposta coletiva, é desejável que o sistema priorize o apoio/compreensão a um grupo e suas decisões em relação ao apoio/compreensão a um indivíduo e suas decisões [3]. Como obter contribuições dos cidadãos em situações marcadas por altos níveis de indeterminação e como processar esse tipo de informação?

Para fins didáticos, suponhamos que um sistema de resposta coletiva seja estruturado em duas etapas simples. O objetivo desse sistema é obter um conjunto de declarações que representem a opinião do grupo sobre um tópico específico.

Na etapa 1, dado um contexto específico, as pessoas expressam suas ideias escrevendo-as em uma declaração breve. Outros membros podem fornecer feedback relacionado a cada declaração, expressando o quanto eles a entenderam. Se necessário, as pessoas podem pedir aos proponentes que ofereçam mais detalhes sobre a declaração. Somente as declarações que alcançam um nível aceitável de compreensão pelo grupo podem ser elegíveis para avançar para a próxima etapa.

Na etapa 2, as pessoas votam em qual declaração representa a opinião do grupo.

Como exemplo, dado o contexto em que as pessoas devem deliberar sobre a evolução da inteligência artificial e seus riscos para a vida humana, uma pessoa poderia escrever a seguinte declaração hipotética:

.

"Nossa sociedade precisa restringir a evolução da inteligência artificial, especialmente quando se trata de questões morais e éticas."

.

Outros membros do grupo são convidados a expressar suas opiniões sobre a declaração. Eles poderiam responder, "Entendo", ou "Não entendo", ou "Ignorar a declaração", optando por não expressar sua opinião.

Isso é semelhante ao que o Pol.is aplicou no exemplo a seguir, um processo para as pessoas expressarem sua opinião sobre os tópicos a serem discutidos em uma assembleia de alinhamento. Os membros têm três opções: concordar, discordar ou ignorar/indeciso.

(Fonte: captura de tela retirada de https://cip.org/blog/alignment)

Essas são certamente contribuições valiosas, mas e se cada pessoa pudesse expressar < seu grau de entendimento >, e, ao mesmo tempo, <o quanto ela não sabe se entende ou não entende>, e <seu grau de não entendimento>? Isso não forneceria uma imagem mais sutil de suas opiniões?

Será que a matemática do "Eu não sei se..." pode auxiliar nesse caso? Que novos insights possíveis poderiam surgir?

.

Neutrosofia

Criada nos anos noventa pelo Professor Florentin Smarandache, a Neutrosofia, aqui chamada carinhosamente de "a matemática do 'Eu não sei se...'", é um ramo da Filosofia que estuda a origem, natureza e escopo das neutralidades, bem como suas interações com diferentes espectros ideacionais, considerando uma proposição, teoria, conceito, evento ou entidade A em relação ao seu oposto AntiA e àquilo que não é nem A nem AntiA, denotado por neutA [4].

.

Uma entidade Neutrosófica abraça três componentes relacionados ao grau de verdade (T), ao grau de indeterminação (I) e ao grau de falsidade (F) de uma declaração.

.

O grau de indeterminação é independente dos outros dois. Cada componente Neutrosofico {T, I, F} pode ter um valor numérico variando de 0 a 1, o que significa que a soma deles está em uma faixa entre 0 e 3. Esse é um tipo específico de conjunto Neutrosofico, chamado Conjunto Neutrosofico de Valor Único (SNVS) proposto por [5].

Dada a declaração hipotética mencionada anteriormente: "Nossa sociedade precisa restringir a evolução da inteligência artificial, especialmente quando se trata de questões morais e éticas"; outros membros poderiam fornecer feedback sobre a declaração, expressando seu grau de entendimento (T), o grau em que não sabem se entendem ou não entendem (indeterminação) (I) e o grau de não entendimento (F).

Uma pessoa poderia dar seu feedback da seguinte maneira:

Meu grau de entendimento em relação à declaração é de 20%, mas há partes da frase que eu não sei se entendo ou não entendo (90%), e há uma parte que eu não entendo (34%).

Alternativamente, o feedback poderia ser escrito como:

"Meus graus de entendimento, indeterminação, não entendimento são, respectivamente, {20%, 90%, 34%}."

Essa frase poderia ser representada da seguinte forma:

Pessoa_1: {0,2; 0,9; 0,34}, equivalente a {T, I, F}

Se houver uma pessoa, 3, ou 500, ou 1 milhão, ou mais, teríamos algo como isto:

Pessoa_2: {0,3; 0,7; 0,1}

Pessoa_3: {0,9; 0,1; 0,2}

Pessoa_n: {Tn, In, Fn}

.

Neutrosofia e o Processo Deliberativo Democrático

Em um processo deliberativo democrático, os membros participantes poderiam concordar previamente que declarações elegíveis requerem um grau de indeterminação menor que um limite. Por exemplo, para que uma declaração seja elegível em um contexto específico, sua Indeterminação deve ser menor que 0,4.

O grupo poderia determinar se há uma porcentagem (51%, ou outro número) de membros no grupo que expressaram um grau de indeterminação maior que 0,4; nesse caso, o membro que propôs a declaração deveria explicá-la melhor para auxiliar outros membros a melhorar seu entendimento e reduzir a indeterminação.

Após o novo feedback, um resultado potencial poderia ser que o nível de indeterminação seja reduzido abaixo do limite e a declaração agora seja elegível. Outro resultado potencial é que o nível de indeterminação permaneça inalterado ou seja reduzido, mas não abaixo do limite. Nesse último caso, os membros poderiam prosseguir para uma nova rodada ou simplesmente registrar o resultado e continuar com o processo deliberativo.

Os membros do grupo poderiam concordar que as declarações que podem avançar para a próxima etapa são aquelas que atingem um nível menor de indeterminação. Neste exemplo, a próxima etapa poderia envolver a votação sobre quais declarações melhor representam o grupo. A matemática neutrosofica também seria usada.

Considerando a mesma declaração 1: "Nossa sociedade precisa restringir a evolução da inteligência artificial, especialmente quando se trata de questões morais e éticas", as pessoas poderiam expressar sua opinião da seguinte maneira:

.

Exemplo de opinião sobre a declaração 1 - Grau de Concordância (30%), Grau de Indeterminação (80%), Grau de Discordância (20%)

.

Vamos supor que os dados na Tabela 1 representam as opiniões de 6 membros sobre a declaração 1. De acordo com a Tabela 1, o grau de concordância é maior do que o de discordância, no entanto, o grau de indeterminação é alto. Quatro membros concordam e dois não concordam. Mas o nível de concordância é baixo, menor que 0,3 para os membros 2, 3 e 5.

Esse tipo de informação torna explícita como a Neutrosofia pode auxiliar as pessoas a refletirem se a Declaração 1 realmente representa a opinião do grupo.

(Tabela 1 - Opiniões de 6 membros sobre a declaração 1 usando a Neutrosofia)

Neste caso, o grupo poderia ter concordado previamente que apenas declarações com um grau de indeterminação menor representariam a opinião do grupo. Esse limite poderia ser inferior a 0,45.

Eles também poderiam concordar que mais da metade mais um dos membros do grupo deveria ter um grau de concordância maior que 0,6. Portanto, após uma nova deliberação, os resultados estão na Tabela 2.

(Tabela 2 - Opiniões de 6 membros sobre a declaração 1 usando a Neutrosophy. Após o 'feedback')

Nesse caso hipotético, a Tabela 2 mostra que o grau de concordância da maioria das pessoas é agora maior que o valor crítico (0,6), o que implicaria que a frase 1 poderia representar a opinião do grupo.

Essas situações e dados hipotéticos são aplicáveis em cenários da vida real. Embora não nos aprofundemos em resultados analíticos específicos neste breve texto introdutório e não técnico, é importante reconhecer sua relevância e significado potencial em contextos práticos.

A Neutrosophy inclui métodos de análise, como estatísticas neutrosoficas e métodos de agregação, entre outros. Neste exemplo, foi utilizada a série Neutrosophic chamada SNVS, que permite a aplicação da Neutrosophy em casos práticos. Podemos explorar a aplicação dessas métricas em publicações futuras.

.

Reduzindo Opiniões Polarizadas

A Neutrosofia poderia reduzir a polarização de ideias, permitindo que as pessoas expressem seu nível de concordância, indeterminação e oposição a um tópico específico, contribuindo para um processo democrático construtivo.

Por exemplo, se a regulamentação da inteligência artificial estiver sendo proposta por dois partidos políticos, uma pessoa poderia expressar sua opinião da seguinte maneira:

Opinião da Pessoa A sobre a proposta do partido político 1 para a regulamentação da IA Concordo com 70%, tenho 50% de indeterminação, discordo em 40%.

Opinião da Pessoa A sobre a proposta do partido político 2 para a regulamentação da IA Concordo com 60%, tenho 40% de indeterminação, discordo em 30%.

Imagine se, em vez de uma pessoa, tivéssemos um grupo de 1000 pessoas deliberando sobre as propostas mencionadas acima. Como a pessoa A, cada indivíduo deve expressar sua opinião considerando ambas as propostas.

Um resultado possível poderia ser o mostrado na Tabela 3.

(Tabela 3 - Opiniões de 1000 pessoas sobre as Propostas de Regulamentação da IA pelos Partidos 1 e 2)

Nesse caso, as pessoas poderiam solicitar mais informações detalhadas do Partido Político 1, devido ao seu alto nível de indeterminação. Se, durante o processo deliberativo democrático, as pessoas decidirem considerar apenas propostas com um nível de indeterminação menor que um limite, por exemplo, 40%, então, de acordo com os dados da Tabela 3, elas também poderiam solicitar informações melhores e mais claras do partido político 2.

.

Ao adotar essa abordagem, a aplicação da Neutrosofia poderia desempenhar um papel significativo na mitigação da polarização de opiniões. A Neutrosofia incentiva os indivíduos a considerar ambas as propostas e expressar suas opiniões nuances sobre o grau de concordância, discordância e indeterminação.

.

Essa metodologia tem o potencial de gerar propostas ou declarações aprimoradas, especialmente em situações caracterizadas por altos níveis de indeterminação, onde os membros requerem informações mais abrangentes para formular uma opinião final.

.

Conclusões

Os processos deliberativos democráticos estão passando por uma transformação evolutiva. Nesse cenário em evolução, é crucial desenvolver metodologias, como sistemas de resposta de inteligência coletiva, que abranjam estruturas matemáticas mais contemporâneas, como a Neutrosofia.

.

A Neutrosofia permite que os cidadãos expressem suas ideias de uma maneira que transcenda escolhas binárias (sim ou não), permitindo uma representação mais natural e inclusiva de sua ambiguidade e indeterminação inerentes. Ao incorporar tais abordagens, podemos incentivar um discurso democrático mais sutil e abrangente.

.

Ao fornecer exemplos simples, os indivíduos podem expressar suas opiniões considerando diferentes graus de concordância, indeterminação e discordância. Essa abordagem permite que as pessoas transcendam a polaridade de opiniões e pode aprimorar significativamente o processo de deliberação democrática.

Esperamos que este texto introdutório possa contribuir para esse processo.

Referências

[1] Landemore, H. 2020. Open democracy. Princenton University Press.

[2] https://pol.is/home

[3] Ovadya, A. 2023. ‘Generative CI’ through collective response systems. https://arxiv.org/abs/2302.00672

[4] Smarandache, F. 1999. A unifying field in Logics: Neutrosophic Logic. In Philosophy. American Research Press, 1–141.

[5] Wang, H.; Smarandache, F.; Zhang, Y.; and Sunderraman, R. 2010. Single valued SVNS sets, Multisp Multistruct 4: 410–413.