a, b, c > 0
Demostrar
1/a³ + 1/b³ + 1/c³ + 3abc ≥ 6
Tenemos una desigualdad en la que intervienen funciones simétricas,
las terceras potencias sobre los valores recíprocos .
Podemos establecer una relación entre los valores, α , y sus recíprocos, 1/α , vía las funciones simétricas unitarias , en .
x ³ − e1 x ² + e2 x − e3 = 0
Construimos la ecuación con soluciones recíprocas,
y ³ − ( e2 / e3 ) y ² + ( e1 / e3 ) y − (1 / e3 ) = 0
Conocido el valor de las funciones simétricas podemos determinar el valor de las sumas de las terceras potencias , ∑1/p³ , mediante las identidades de Newton.
3 e3² − 3 e1 e2 e3 + e2³
∑1/p³ = ――――――――――――
e3³
Podemos expresar la desigualdad original como,
∑1/p³ + 3 e3 ≥ 6
3 e3² − 3 e1 e2 e3 + e2³
―――――――――――― + 3 e3 ≥ 6
e3³
La siguiente desigualdad entre las funciones simétricas unitarias ,
n
en ≥ ( ) emm / n
m
1 ≥ m ≥ n
nos permite resolver el problema, expresando e1 y e2 en función de e3 ,
e1 ≥ 3 e31 / 3
e2 ≥ 3 e32 / 3
Sustituyendo y simplificando,
e3 + 1 / e3 ≥ 2
Hemos transformado el problema original en una desigualdad que puede verificarse empleando las propiedades de las medias aritmética/geométrica, que es evidentemente cierta, de forma que queda demostrada la validez de la desigualdad bajo estudio.
∎
Media
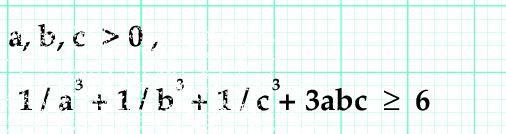
Congratulations @j2e2xae! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 400 comments.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts: