Saludos amigos de la comunidad académica y científica de hive.
En esta ocasión quiero socializar con ustedes un tema muy importante dentro de la ingeniería y los temas que se tratan en cálculo a nivel universitario, como es el caso del cálculo de volumen empleando una de las aplicaciones que tiene la integral como es el caso del método de discos, veamos de que trata todo el asunto.
Cuando hacemos girar la gráfica de una función alrededor de un eje se genera lo que se conoce como un sólido en revolución, este sólido en revolución por ende va a tener un volumen generado, el cual se puede calcular por medio de integrales mediante el método de discos.

En el caso de la imagen anterior estamos observando un sólido en revolución, ahora bien quizás muchos de ustedes se pregunten, ¿Por qué es un sólido en revolución? simplemente por el hecho de ser un cuerpo geométrico obtenido de la rotación de un círculo, es importante recalcar que estos sólidos en revolución se obtienen al hacer girar una parte de la gráfica del plano alrededor de una línea recta fija.
Ejemplo del cálculo del volumen de un sólido en revolución por medio del método de discos
El ejemplo que quiero traer a acotación en este post está relacionado al cálculo del volumen de un sólido en revolución por medio del método de discos con integrales, teniendo en cuenta que el eje de giro es el eje x. Para ello tenemos la siguiente fórmula:
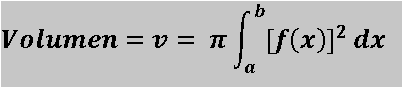
Para la ecuación planteada, si es una función la que se está haciendo girar alrededor del eje x, entonces a y b serían los cortes con el eje x de dicha gráfica, y f(x) sería la función que se está haciendo girar alrededor del eje x, el número pi que multiplica la integral funcionará como una constante multiplicativa.
Tomemos en cuenta el siguiente ejercicio para que entendamos cómo se calcula este volumen:
Encontrar el volumen del sólido formado al girar la región acotada por la siguiente función:
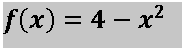
y el eje x mediante el método de discos.
Para que veamos el sólido que se forma, voy a mostrarles la gráfica de la función parabólica:
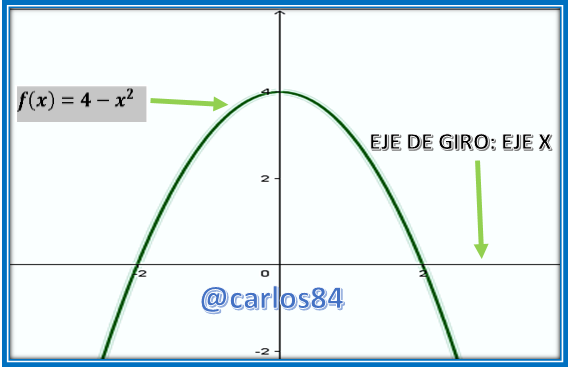
En la imagen anterior podemos ver las condiciones del gráfico del sólido en revolución que se obtiene al hacer girar la porción del gráfico del plano perteneciente a la parábola y el eje x. El sólido en revolución que se obtiene es el siguiente:

Para calcular el volumen procedemos de la siguiente forma:
Como la gráfica es simétrica respecto al eje y, simplemente tomamos como a=0 y b= 2 y multiplicamos la integral por 2, por lo tanto me queda que:
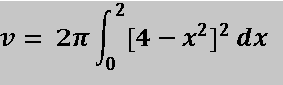
Procedemos a resolver el producto notable del integrando:
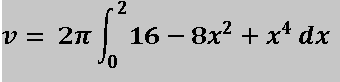
Resolvemos la integral y aplicamos el teorema fundamental del cálculo:
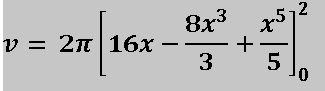
Al aplicar el teorema fundamental del cálculo debemos recordar que se sustituye el límite superior menos el límite inferior, sin embargo como el límite inferior es igual a cero, solo hacemos la sustitución del límite superior:
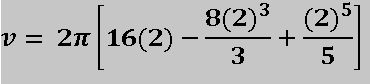
Finalmente realizamos los cálculos algebraicos y se obtiene que:
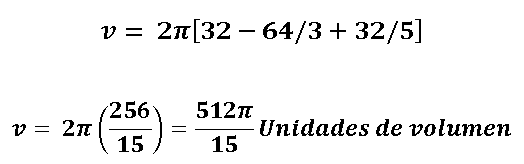
Si damos un resultado más exacto incluyendo decimales pudiéramos estar diciendo que el volumen del sólido en revolución cuando se hace girar alrededor del eje x la función parabólica en mención es de 107,23 unidades de volumen.
Conclusión
Podemos ver evidenciado como una vez más las integrales tienen una aplicación más en ese mundo diverso de aplicaciones, en donde también a parte de cálculos de áreas también podemos realizar cálculos de volumen, para este caso el cálculo de volumen del sólido en revolución generado al hacer girar sobre el eje x una función parabólica.
Espero que este contenido sea de gran utilidad, esperando que en esta cuarentena social y clases virtuales a distancias, los interesados en el aprendizaje de este tipo de contenido puedan sacarle el mejor de los aprendizajes.
Referencia recomendada
Cálculo completo Vol 1 y 2 9na Edición Ron Larson & Bruce H. Edwards
¡interesante! gracias por compartir tu post para la comunidad.
Hola @audrisbg.
Gracias a ti por leer el post y comentar. Saludos
Su post ha sido valorado por @ramonycajal
Gracias por el apoyo a @ramonycajal y @cervantes. Saludos