Greetings fellow mortals!! I hope everyone is alright!

Today we gonna explore the odds of the first few steps in the game: draw the opening hand, mulligan of unwanted cards and drawing the first card in your turn. We wish to know what are the chances to get that game-winning legendary card (=Chiron, The Teacher in our case) on these first oportunities.

This post is the part 1 of 2 which contains some theory of statistics and conclusions about the chances to get a legendary from your deck at the start of the game. Thus, you can skip ahead to conclusion if you want to jump the methodology and go straight to results.

In the part 2 we'll do a validation through an experiment to check our findings (and the game's random number generator).

Finding a map to seek Chiron: The theoretical values

We are interested in get our legendary or any other singleton (=1 copy only) card right from the get go, on the first turn of the game. To accomplish this feat, we have three oportunities: our opening hand of 3 cards, three mulligans (or four if second player) and the card draw from our first turn.

We're going to use probability theory to reach the odds. Let's get started

Probability of an event

An event is all the outcomes that we are interested. Take a coin for example, there're only 2 outcomes: Heads (H) or Tails (T). If we wish to know the chances to get Heads in a single coin flip, our event (let's call it event A) contains the outcome "the coin is H", or just A=[H]. Assuming that our coin is fair, the odds of our event A happening in a single coin flip is:

P[A] = (n. of outcomes in A)/(total outcomes) = 1/2 = 50%

We read this as "the propability of happening the event A (getting Heads in our case) is equal to the number of outcomes in our event A (=1 -> get 1 H) divided by the total number of outcomes (=2 -> the coin can be H or T)".

The same thing happens to a deck of cards. We have an event which consists in getting Chiron (our desired outcome) inside an universe of all the cards in our deck (=30 at the beginning of the game). Thus, if we want to calculate the odds of get Chiron in the first card we draw in the opening hand:

P[Chiron] = (n. of Chiron in our deck)/(total cards in our deck) = 1/30 = 3.33%

We see the odds of our first card drawn be Chiron is 3.3%, so the odds of not draw a Chiron is (29/30) = 96.7%

That's nice, but what about the chances of draw Chiron in the second card of the opening hand if we miss the first? And in the opening hand as a whole?

Sequence of outcomes

Let's back to the coins. Instead of flipping one coin, we can flip two coins, and our desired event is getting at least one H.

So, let's flip the first coin. We already know the chance of get a H is 50%. If we trully get a H, it doesn't matter the result from the second coin because we already got a H. But what if we miss the first?

Then we toss the second coin. But there's a catch. We flip the coin if we miss the first, and there's a probability for that to happen, which is the probability for the first coin gets a T, that we also know it's 50%. Then we toss the second coin expecting a Heads. We write that as a TH inside our desired outcomes, which reads to "Tails on the first toss and Heads on the second".

Our event now becomes A: [H, TH], "Heads on the first and don't care about the second OR Tails on the first and Heads on the second". Since there's a sequence of outcomes in the TH part, we need to multiply both probabilities to get our result for that:

P[TH] = P[T first toss] * P[H second toss] = (1/2) * (1/2) = 0.5 * 0.5 = 0.25 = 25%

Now we have the two values for the outcomes of our event A:[H, TH]. 50% of get H on the first coin toss or 25% of get T on the first and H on the second. Our total probability is the sum of both:

P[A] = P[at least one H] = P[H] + P[TH] = 50% + 25% = 75%

Probability to get a legendary on the opening hand

We can apply the exact same thinking to our Chiron case: If we draw it on the first card, we don't care about the other 2 cards (I'll call it a Hit and don't care as x), or we miss the first and draw on the second and don't care the third card (a Miss, a Hit and x), or we miss both draws and hit on the third (a MMH).

Our event Chiron becomes: [Hxx, MHx, MMH].
Now we need to find the probabilities of each part. The first one (Hxx) we already did it, hit the Chiron on the first draw is 3.33%.
About the second, we have to remember that after we draw our first card and it misses (we draw any of the 29 cards that aren't Chiron), our deck now has 29 cards remaining instead of 30. When we don't care about what we draw, any card is ok to us, so:

P[MHx] = P[M] * P[H] * P[x] = (29/30) * (1/29) * (28/28) = 3.33%

Finally, our third element is:

P[MMH] = P[M] * P[M] * P[H] = (29/30) * (28/29) * (1/28) = 3.33%

And the total probability to draw Chiron on the opening hand of 3 cards is the sum of each element:

P[Chiron in the opening hand] = 3.33% + 3.33% + 3.33% = 10% [ta-da 😄]

---

Probability to get a legendary in the mulligan step

If we miss Chiron in the opening hand (and the chances are big, 90%), it's possible to perform a series of mulligans cutting unwanted cards from the hand. The cut card is set aside and doesn't return to our deck, it also cuts the second copy of the card from the deck, according to @copperpitch's video about mulligan (tip n.4).

In summary, if you set aside a singleton card (=1 copy only), your deck will be 1 card smaller. But if you cut a double card (=2 copies in the deck), your deck will be 2 cards smaller (1 from hand and 1 from the deck, if any).

Worst case: mulligan away only singleton cards

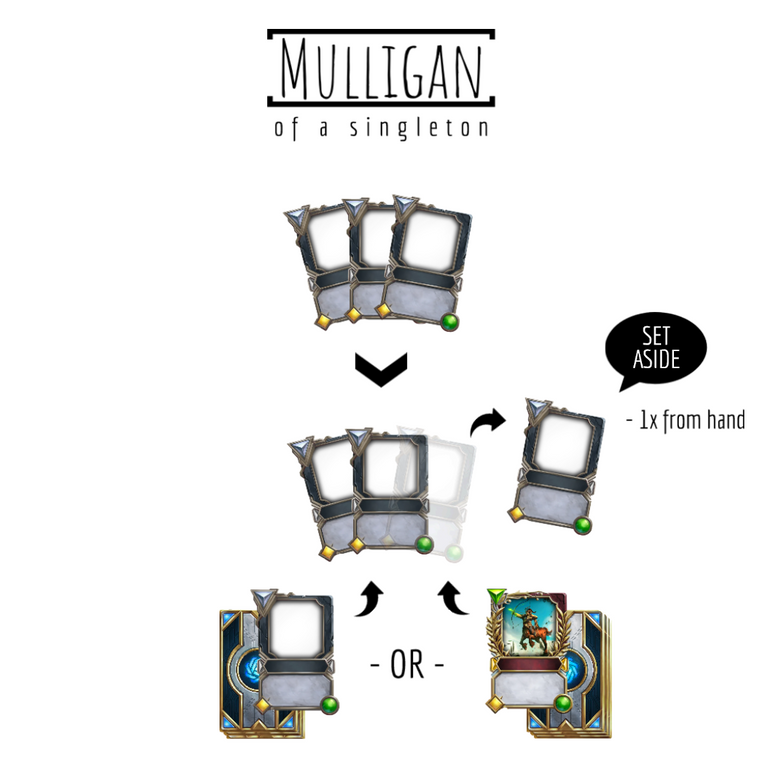
Our worst case scenario is cut only singletons on all our mulligans. Remember: we only try a mulligan if we fail to hit Chiron. Our first mulligan probability becomes the event M1: [Miss opening hand and Hit on the first mulligan]. To Miss our opening hand, we have to Miss all the three cards drawn. So our event M1: [MMMH]:

P[M1] = P[MMMH] = (29/30) * (28/29) * (27/28) * (1/27) = 3.33%

Our deck get 1 card smaller on each mulligan, because the card drawn is on our hand OR is set aside.

The same thinking happens on the following mulligans: if we don't hit Chiron, we perform another mulligan. So, hitting Chiron on M2 is [MMMMH] and so on. The probabilities of each is below:

P[M2] = 3.33%
P[M3] = 3.33%
P[M4] = 3.33%

If you are the first player, you can perform up to three mulligans, and the odds to get Chiron on the mulligan step is M1 + M2 + M3 = 10.0%.

But if you're the second player, you have one more mulligan, and the odds becomes M1+M2+M3+M4 = 13.3%

Best case: mulligan away only double cards

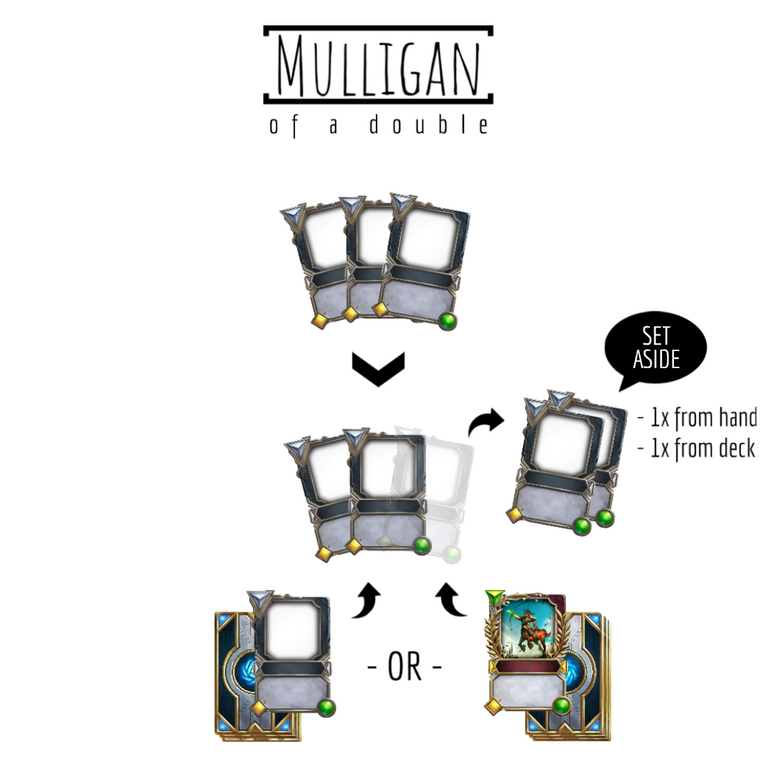
The best scenario is to set aside a double card on every mulligan we get. The thinking is the same as the case with singletons, but now our deck becomes 2 cards smaller on every attempt, which slightly rises the odds of finding Chiron.

Our event M1 (=1st mulligan) is the same as before: [Missing Chiron on the opening hand and Hit it on the first mulligan] = [MMMH] but now our deck has 26 cards remaining when we try to draw Chiron (2 are in our hand, 1 we set aside from our hand + 1 from our deck):

P[M1] = P[MMMH] = (29/30) * (28/29) * (27/28) * (1/26) = 3.46%

If we fail again to find Chiron, 2 more cards are removed from the total and so on. he probability to hit Chiron on the remaining mulligans are:

P[M2] = 3.61%
P[M3] = 3.77%
P[M4] = 3.96%

Again, if you're the first player, you have up to three mulligans and the odds of finding Chiron on your mulligans attempts is 10.8%

But if you're the second player and the rights to perform four mulligans, the chances rises to 14.8%.

---

Probability to get a legendary in the first card draw from the turn

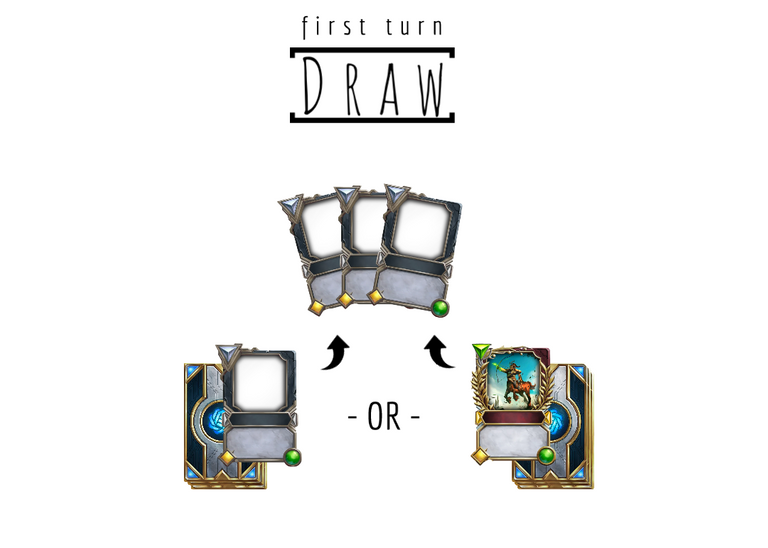
This is the last step. Before the game actually begins for almost all matches, each player draws one more card: the draw for the first turn. So we have a last chance to find that pesky Chiron if we couldn't so far.

If are're thinking that the odds is to Miss our opening hand, and Miss all the mulligans and Hit it on the first card draw, you are right! But this time, when we draw, there're no cards set aside, so our deck has 27 cards remaining again (30 at the start - 3 in our hand).

But before proceeding, let's remember one more tip. The odds of Missing Chiron and Hitting Chiron sum to 100%, always. Thus:

% Missing Chiron = 100% - % Hitting Chiron

Which will be nice to know later.

Worst case scenario again

So far we calculated all the odds to find Chiron: 10% from the opening hand and 10% from the mulligan in the scenario of singletons (or 13.3% if second player). Putting our new knowledge to work, we can calculate the chances of missing Chiron up to our first card draw from the turn, and use this value to get the probability to find the legendary card in the first turn draw (just remember that our deck has 27 cards now when we draw the first one).

If you're the first player:

P[Missing Chiron so far] = 100% - 10% (Hitting in the opening hand) - 10%(Hitting in the mulligans) = 80%

And finally, the probability of draw Chiron in the first turn draw is simply:

P[Missing Chiron so far and Hit on the first draw] = 0.8 * (1/27) = 2.96%

In the case you're the second player:

P[Missing Chiron so far] = 100% - 10% (Hitting in the opening hand) - 13.3%(Hitting in the mulligans) = 76.7%

and:

P[Missing Chiron so far and Hit on the first draw] = 0.767 * (1/27) = 2.84%

Best case scenario again

We now apply the same procedure for the best case (=set aside only doubles during the mulligans).

If you're the first player, the chances of find Chiron in the first card draw:

P[Missing Chiron so far and Hit on the first draw] = [1.00 - 0.1(Hitting in the opening hand) - 0.108(Hitting in the mulligans)] * (1/27) = 2.93%

And if you're the second player, the chances are:

P[Missing Chiron so far and Hit on the first draw] = [1.00 - 0.1(Hitting in the opening hand) - 0.148(Hitting in the mulligans)] * (1/27) = 2.79%

---

The map to find Chiron: Adding everything together

Now we have all the pieces to come up with the final probability to get any legendary or singleton card in our hand at the start of the game. The secret is adding all the probabilities, splitting the worst and best scenarios, and for first and second player.

For the worst case:

[1st Player]: P[Draw a Legendary at the start of the game] = 10.0% + 10.0% + 2.96% = 23.0%
[2nd Player]: P[Draw a Legendary at the start of the game] = 10.0% + 13.3% + 2.84% = 26.1%

In theory, we have the same probability of being first or second player. So, on average:

Draw a Legendary at the start of the game = (23.0 + 26.1)/2 = 24.5%

For the best case:

[1st Player]: P[Draw a Legendary at the start of the game] = 10.0% + 10.8% + 2.93% = 23.7%
[2nd Player]: P[Draw a Legendary at the start of the game] = 10.0% + 14.8% + 2.79% = 27.6%

On average:

Draw a Legendary at the start of the game = (23.7 + 27.6)/2 = 25.7%

Conclusion: The chances of a Legend

To sum up all we did today, let's check our main findings when you try hard to dig up that must-have-on-turn1 legendary card from your deck:

• The chances of starting the game with a legendary in hand is between 24.5% and 25.7%, depending if you set aside all singletons or all doubles in your mulligans;
• Your odds is greater if you're the second player with a deck of singletons [26.1%] than the first player with a concise deck of doubles [23.7%] (excluding the legendary card). Which means one more mulligan is a bit better than a concise deck, inside the concept of starting the game with a legendary;
• No matter your deck composition nor if you go 1st or 2nd player, if you play a lot of matches, it's expected to get the legendary card once every four matches if you mulligan hard to get it (but there're chances you can go up to 10 matches and never see it at your starting hand).

I hope you liked this post, this is the first part of a two-part journey. On the next post, we gonna try to prove one of these numbers through an experiment on the solo play.

If you enjoy this type of content, let me know and I'll try to bring new stuff related to statistics or data crunch.

See you on the part 2!