
ENTANGLEMENT AND OTHER ODD THINGS
You may have heard about entanglement already, most probably even in a romantic fashion...but what is it, for real?
When your are dealing with a system composed by more than a qubit, it may happen (how it happens, it really depends on what system you are considering) that those qubits are interacting with each other creating a strong correlation: entanglement, indeed!
From a mathematical point of view, this fascinating phenomenon is somehow related to the superposition principle.
Preliminarily, let us say that we have two qubits, each one in the state

where 1, 2 refers to first and second qubit, thus we write the total state of the two qubits combined
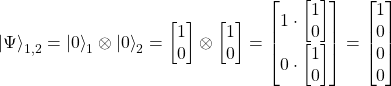
roughly, it means that when you have a new state out of two different qubits, you obtain as a state a new vector with four components.
In fact, you can build a new vector space for states composed by two qubits (and more, using the same procedure), that has as a basis four different orthogonal vectors
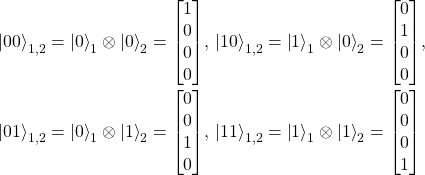
Nonetheless all the math, the qubits in the state we wrote are not entangled, because, formally, a state is entangled when you cannot write it in terms of two distinct vectors, i.e.
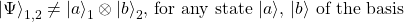
Things change when we consider, for example, a system in the following state
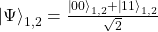
here there is entanglement! Indeed, there is no way to rewrite the total state as a product of two vectors of the basis.
After a lot of math, now we have an entangled state. What do we do with it and what's special, after all?
Stuff is turning interesting when you measure an entangled state.
More precisely, when you measure the distinct components of an entangled state: because an entangle state still retains separate its components (in space or time), since they are not physically fused together!
In other words, if you entangle two photons or two atoms, you still have two photons or two atoms, you simply don't know in which state are the two qubits.
But now you are taking your fancy lab equipment, you measure some physical property of your qubits (e.g. the spin of your two electrons) and you realise that, when you have entangled electrons, something "magical" happens.
You measure one qubit, you obtain that the electron is in state 0 (whatever it means). Then, you measure the spin of the other and you obtain 1.
You repeat this experiment thousands of time and you see that you always obtain two orthogonal results: if the first qubit is in state 0, the second one is in state 1, and vice versa.
Moreover, you decide to conduct a similar experiment with your friend living on the Moon (who does not have a friend living on the Moon, nowadays 😂).
You prepare a couple of entangled photons: one for you and one to send to your friend on the Moon.
You measure (for example) the polarisation of your photon and you get state 1 (again, whatever it means). Then you call your friend, you say what measurement you performed (not the result) and he/she tells you that he/she gets from the same measurement, but performed on his/her photon, the state 0.
Repeat the experiment and you will always get correlated results!
That is the "magic" of entangled qubits: this correlation holds at any distance and it gives an "instantaneous" result (for more details about this problem, search for "EPR" paradox)!
That's all for today!
Stay tuned and see you in the next post! We will see how to draw a QUANTUM CIRCUIT using QUANTUM GATES.
Follow @maar to stay updated and to know more about the fascinating world of Quantum Information and Computation!
