
THE QUBIT
In this episode, we introduce the concept of quantum bit, called qubit, that is necessary to build quantum computers as much as bits are needed for classical computations.
Indeed, a classical bit is the minimum information resource to let your laptop and your smartphone work: it can be 0 either 1, the basis of the binary representation.
In our "classical" computers, bits are encoded in electric signals processed by some fancy devices like transistors, memory switches, etc.
So, basically, when you are texting, scrolling your social media feed, watching a video, or anything else, there are in your device electric signals going through some logical gates and a computation is performed by the "evolution" of those signals into the device itself.
Now, think about a qubit, the minimum information resource for a quantum computer, as a bit that can be simultaneously 0 and 1 (yes, like for the famous Schrödinger cat! For example, you may say that 0 means "alive" and 1 means "dead").
There are many processes and systems in which you may encode qubits, but in general you may have any two-level system (electron spin, "special" atomic energy levels, photon polarisation, etc.) as a qubit.
A little bit more formally, a qubit is a vector in a bi-dimensional complex space, in which we define a basis (a couple of vectors) generating all the space
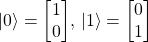
In other words, in a bi-dimensional space you only need two distinct orthogonal vectors in order to be able to write every other possible vector in that space.
Here the superposition of the cat's states "alive" and "dead" comes forth: because of the structure of this kind of vectorial spaces, an arbitrary state (i.e. a qubit) can be expressed as a superposition of the vectors of the basis, as follow
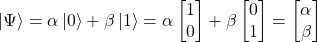
where α, β are complex numbers such that
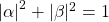
This requirement determines that all the vectors in this space are unitary, in particular it is convenient to write an arbitrary state as
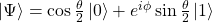
as you can see, now a quantum state have a more familiar face and it only requires two angles to fully characterise such a state.
All the infinitively many vectors that can be written in this form, they draw a special sphere, called Bloch sphere
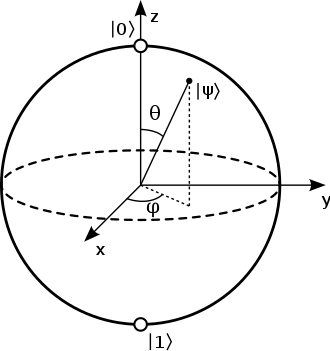
On this sphere, given the two angles, it is easy to find a quantum state and to visualise rotations applied to the state. But about the latter, we will discuss in an other episode.
That's all for today!
Stay tuned and see you in the next post! We will talk about ENTANGLEMENT!
Follow @maar to stay updated and to know more about the fascinating world of Quantum Information and Computation!
