Hi there. In this math post, I cover multiplying rational expressions. You can have easy cases all the way to more tougher algebraic cases. It is assumed that the reader is comfortable with distributive law, binomial expansion and factoring polynomials for the harder cases.
Math text rendered in LaTeX (lay-tech) with the use of QuickLatex.com.

Topics
- A Review of Multiplying Fractions
- Multiplying Rational Expressions
- Harder Cases
A Review of Multiplying Fractions
When it comes to multiplying fractions we have the general case of:

Multiply the top to get the result on the top part of the fraction. To obtain the bottom (bd), multiply the bottom quantities only.
Example One
What is one half multiplied by three fifths?
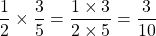
Example Two
What is two sevenths multiplied by nine tenths?
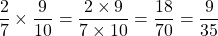
It is common practice to reduce fractions to lowest terms.
Multiplying Rational Expressions
There are cases where numbers are not known. You would have variables instead of numbers to represent unknown quantities. Common variables include x, y, k, z. Let's look at a few examples.
Example One
Simplify 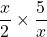 .
.
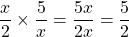
Alternatively, you can cross reduce with x variable to obtain the answer of 5 halves.
Example Two - Distributive Law
Simplify 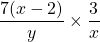 .
.
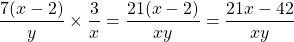
The fraction can be split into two separate fractions separated by the minus sign. The first fraction has the x variable eliminated.

Example Three - Multiplying Binomials
Complete the multiplication in 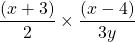 .
.
As usual, multiply the numerators to obtain a new numerator. The denominators multiplied together yields 6y.
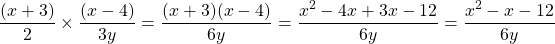
In this example I have shown multiplying binomials. It is preferable to leave it as factored form in general.

Harder Cases
These things can get really difficult in terms of the algebra. Those with good algebra skills will spend less time multiplying these correctly. It is like getting good at cutting vegetables. Better algebra skills allows for doing more in less time.
Here are a few more difficult cases.
Example One
Multiply and simplify 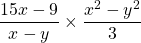 .
.
When it comes to this type of case avoid a brute force approach where you multiply the fractions together. Try to see if you can reduce or cross-reduce the fractions.
The numerator in the left fraction has a common factor of 3. This numerator can be factored into 3(5x - 3).
From the right fraction, the numerator is a difference of squares and can be factored accordingly.
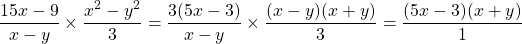
The (x - y) factors cancel each other out and the 3 factors are cancelled out too. This leaves with (5x - 3)(x + y). You could multiply these two binomials but leaving it is good enough.
Example Two
Multiply and simplify  .
.
It is a good idea to start with factoring the numerator from the right fraction.
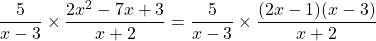
The (x - 3) can be cross cancelled and the two fractions can be multiplied together.
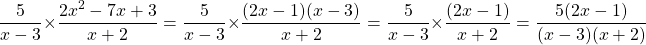
As an optional step, the 5 from the numerator can be distributed to (2x - 1) to obtain 10x - 5.