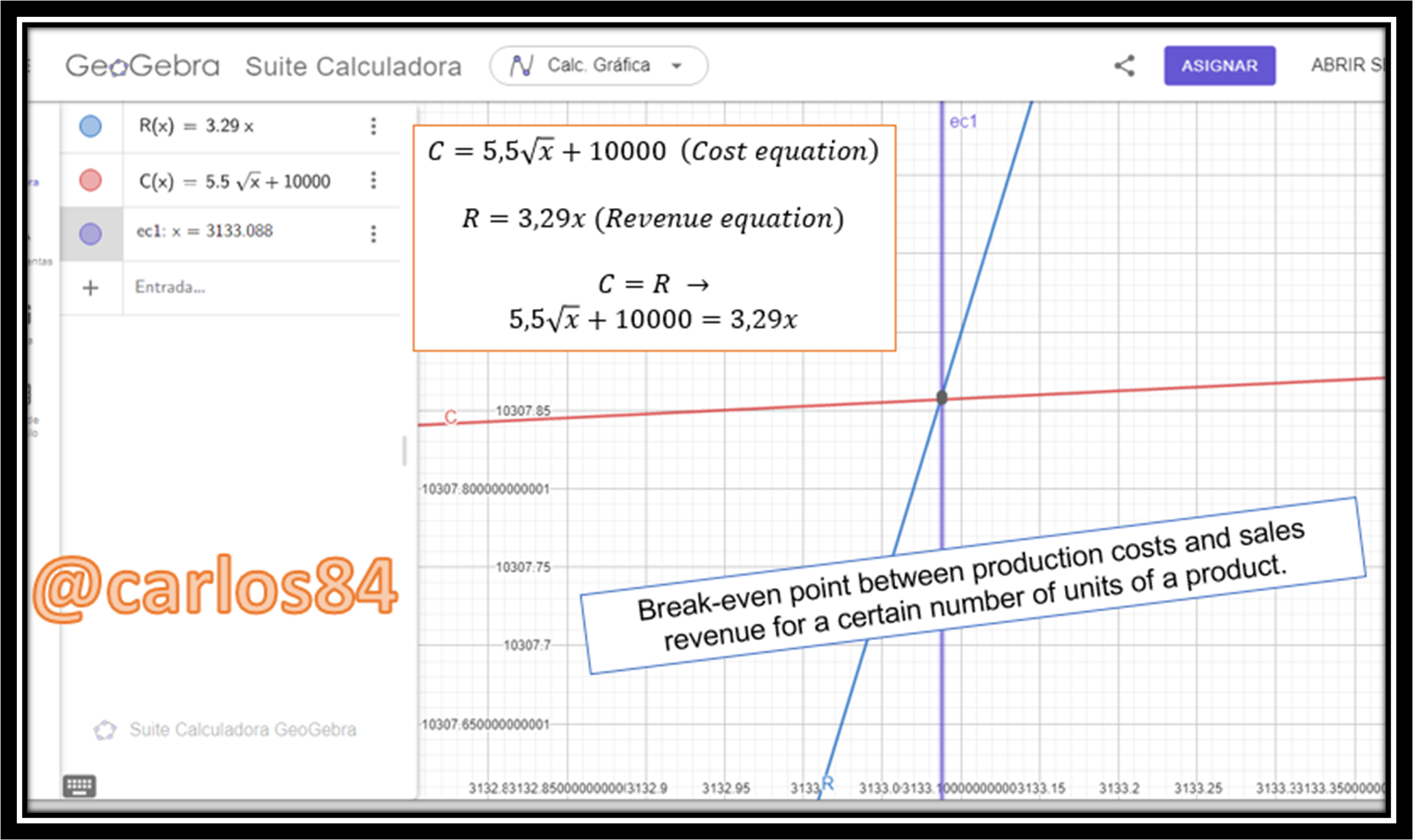
Hello friends and followers of STEM content. In this opportunity I want to explain the way in which you can solve a problem where you are asked to find the break-even point between the sales that can be made of a certain product when it finds the equilibrium, that is, when sales are equal to the cost of producing a certain amount of the product.
Problem
Calculate the sales required to reach equilibrium (R=C) if the production cost C of x units is:

Solution to the problem
Since the break-even point is when the revenues from product sales are equal to production costs (R=C), then we must start from:

For such a second degree equation, we find the value of x as follows:

Since it is giving us two values of the x units of the product, we will take the value of x2, since that value is the one that best represents the value of the sales revenue of the product.
Conclusion
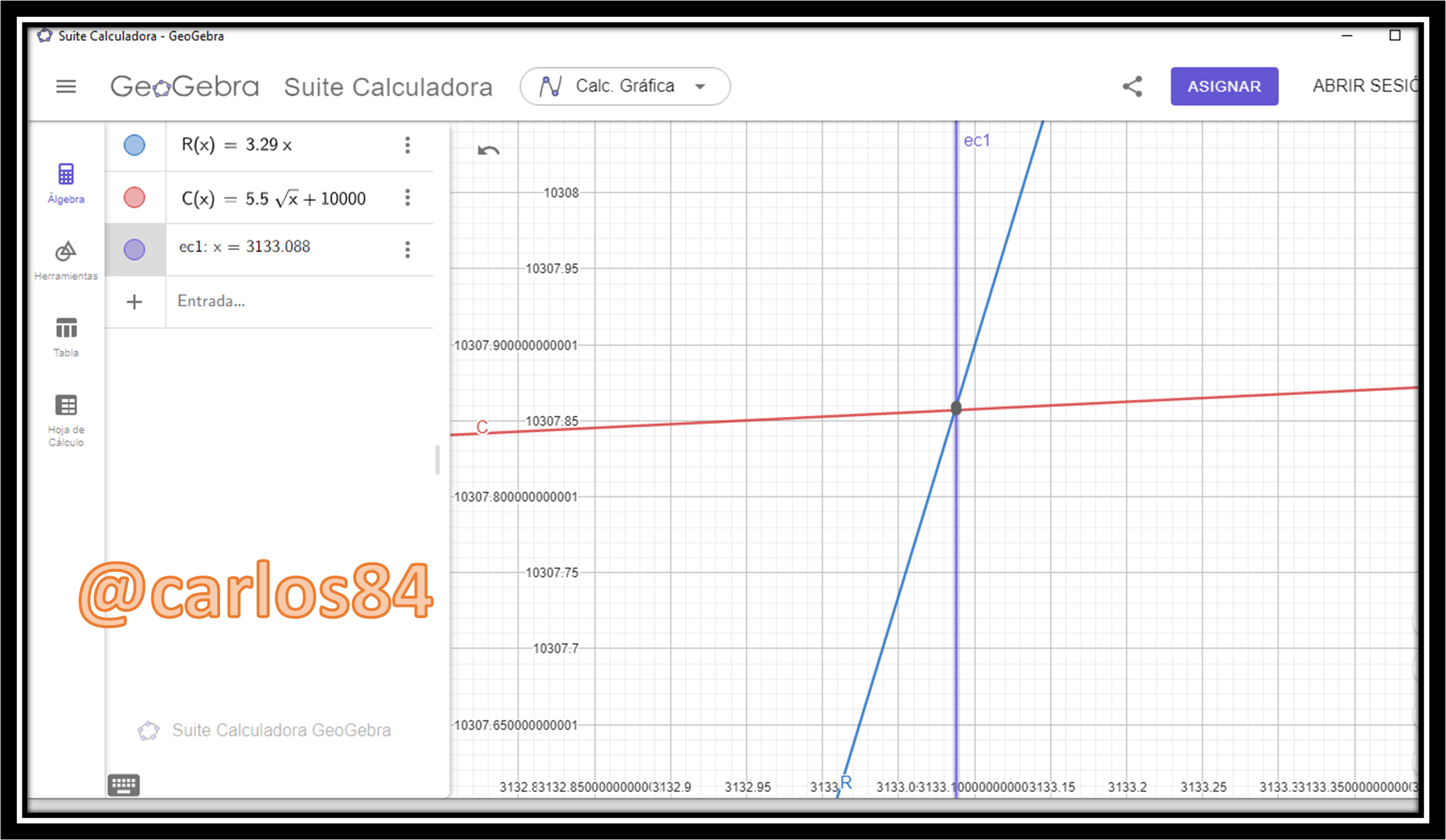
The sales revenue of x units of the product so that equilibrium can be reached, i.e. for when sales revenue equals production costs is when sales revenue of 3132.99 units of the product is obtained, which could be equivalent to 3133 units of the product.
The graphical representation of the break-even point is:
Recommended reference
Larson and Hostetler's Book of Calculus with Analytic Geometry. Volume I.
Note: The equations were elaborated using the equation insertion tools of Microsoft PowerPoint. The graph was elaborated using GeoGebra software.