En la ingeniería cualquier cantidad física puede medirse mediante Escalares y Vectores.
- Escalares: es la expresión de la magnitud de cualquier cantidad física, ya sea positiva o negativa. La longitud, la masa y el volumen son ejemplos de una cantidad escalar.
- Vectores: es cualquier cantidad física que requiere de una magnitud y de una dirección. Un vector se representa gráficamente mediante una flecha. La longitud de la flecha representa la “magnitud” del vector y el ángulo entre el vector y un eje fijo (eje cartesiano, polar, etc) define la dirección de su línea de acción. La punta del vector se indica con una flecha para dar el “sentido de dirección”.
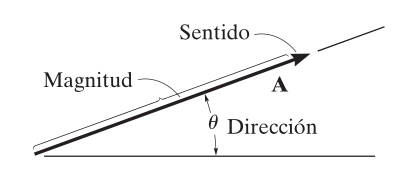
Operaciones de Escalares y Vectores
Las operaciones vectoriales van desde la suma, resta, multiplicaciones , etc.
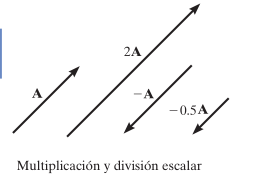
Multiplicación y división de Escalares y Vectores
Si un vector se multiplica por un escalar positivo, su magnitud se incrementa en esa cantidad. Cuando se multiplica por un escalar negativo también cambiara el sentido de la dirección del vector.
Suma de Vectores
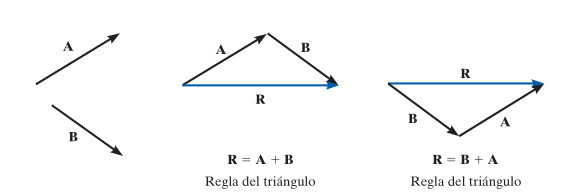
Los vectores obedecen la ley del paralelogramo para la suma. El cual se describe de la siguiente manera:
- Primero, uniremos las colas de los componentes en un punto de manera que se hagan concurrentes.
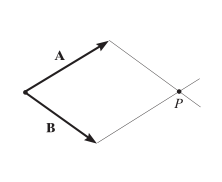
- Desde la cabeza de B, dibuje una línea paralela a A, y desde A dibujemos una línea paralela a B. Estas dos lineas se intersecan en el punto P de esta forma es que se obtiene un paralelogramo.
- La diagonal de este paralelogramo que va desde la concurrencia de los dos vectores hasta el punto P forma la Resultante “R”
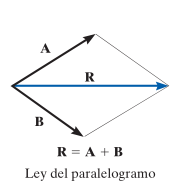
La ecuación final de este método es R=A+B, sin embargo no es el único método, también existe la regla del triángulo, que explica que la Resultante se puede obtener de trasponer el vector B en la cabeza del vector A, o bien, la cola del vector A en la cabeza del vector B. Quedando de la siguiente manera:
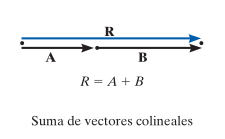
En el caso de que los dos vectores tengan el mismo sentido, es decir, son colineales entonces la suma de los vectores se reduce a una suma simple algebraica trasponiendo un vector después del otro.
¿Ahora que pasa con las restas?
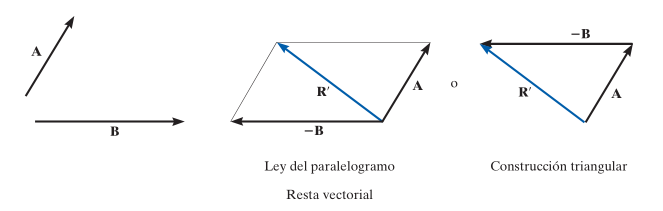
En el caso de las Restas de vectores solo cambiará el sentido de la resultante, puesto que seguirá siendo una suma pero en sentido opuesto. Veamos como actúan dependiendo el método usado.
A continuación veremos ejemplos empleados en situaciones reales mediante la aplicación de la ley del paralelogramo.
Ejemplo 1
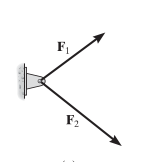
Nos encontramos con dos fuerzas interactuando en un pasador, para poder hallar la fuerza resultante “Fr” se traza una coincidencia paralela de cada vector quedando de la siguiente manera. Fr = F1 + F2.
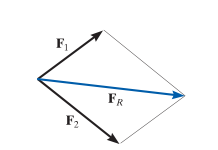
Entonces al tener esta construcción podemos simplificarla con la ley del triángulo y aplicar la ley de cosenos o ley de senos y obtener la magnitud de la fuerza resultante.
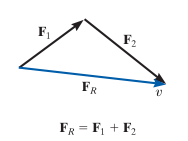
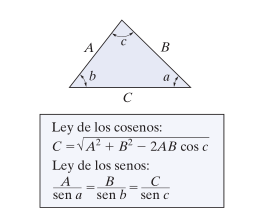
Este tipo de situaciones son muy comunes, por ejemplo al tensar dos cadenas para soportar una carga, o calcular los esfuerzos generados por una polea, etc.
Notas
- Un escalar es una cifra positiva o negativa
- Un vector es una cantidad que tiene magnitud, dirección y sentido.
- La multiplicación o la división de un vector por, o entre, un escalar cambiará la magnitud del vector. el sentido del vector cambiará si el escalar es negativo.
- Como un caso especial, si los vectores son colineales, la resultante se forma mediante una suma algebraica o escalar.
Galería y Bibliografía


Publicado en Guía de Mecatrónica, mas artículos como estos sigueme o visita mi web
Congratulations @guia-mecatronica! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
STOP
Notifications have been disabled. Sorry if I bothered you.
To reactivate notifications, drop me a comment with the word
NOTIFY