If two vectors 'A' and 'B' are represented by the two adjacent sides of a parallelogram (both in direction and magnitude) in different order, then the resultant 'R' is represented by diagonal of the parallelogram (both in direction and magnitude).
So, R=√(A^2 + B^2 + 2ABcos p)
Proof : OBCA is a parallelogram
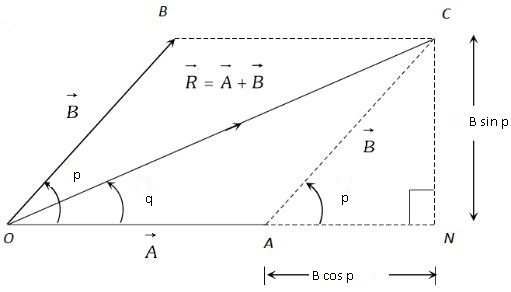
In ∆ ONC
OC^2 = ON^2 + NC^2
=> R^2 = (A + Bcos p)^2 + (Bsin p)^2
=> R^2 = A^2 + (Bcos p)^2 + 2ABcos p + (Bsin p)^2
=> R^2 = A^2 + B^2 + 2ABcos p
=> R = √(A^2 + B^2 + 2ABcos p)
Note : sin^2 p + cos^2 p = 1
Excellent. That shows you have understood the concept. It will surely be helpful to u and others.