▶️ Watch on 3Speak - YouTube - Odysee - BitChute - Rumble - PDF notes
In this video I go over a complete derivation of the cubic formula, which is a solution to the cubic equation. This proof utilizes the PQ substitution method, which I first demonstrate by solving for the quadratic formula. Using this substitution method, we can write the cubic equation in the form that we can then apply Vieta's substitution, which converts it into a quadratic equation. Now we can start going backwards and putting our solutions back into the previous substitutions. This involves a cube root, which gives 3 solutions and which we determine via the cube root of unity. Two of the solutions involve complex numbers, but fortunately the resulting 3 solutions in the cubic formula simply interchange the positive and negative signs of the complex numbers. While there is a ton of algebra, many terms repeat themselves so I just copied and pasted to save time. If you like math proofs, you'll love this one!
Note that I followed derivation by @blackpenredpen :
Time stamps
- Intro: 0:00
- Recap on Quadratic equation and formula: 0:40
- Cubic Formula: 3:58
- Derivation of Cubic Formula: 5:46
- Step 0: Solve Quadratic Formula using PQ Substitution: 6:00
- Step 1: Get rid of square power term using PQ Substitution: 12:44
- Recap on Pascal's Triangle: 18:39
- Applying the substitution: 20:22
- Step 2: Apply Vieta's Substitution to obtain a quadratic equation: 28:04
- Step 3: Find First Solution of y: 39:17
- Step 4.1: Cube Root of Unity: 48:24
- Complex factors are rotations in the complex plane: 1:00:10
- Step 4.2: Find the other solutions for y: 1:05:26
- Step 5: Put Everything Together to solve for x: 1:13:31
- Double check and summary: 1:25:37
- Outro: 1:27:27
Video sections playlist
View Video Notes Below!
Become a MES Super Fan - Donate - Subscribe via email - MES merchandise
Reuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically.
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books: "Where Did the Towers Go?" by Dr. Judy Wood
Join my forums: Hive community - Reddit - Discord
Follow along my epic video series: MES Science - MES Experiments - Anti-Gravity (MES Duality) - Free Energy - PG
NOTE 1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial- Download and read video notes.
- Read notes on the Hive blockchain $HIVE
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations: Increase video speed - Increase video audio - Text to speech (Android app) – Archive webpages
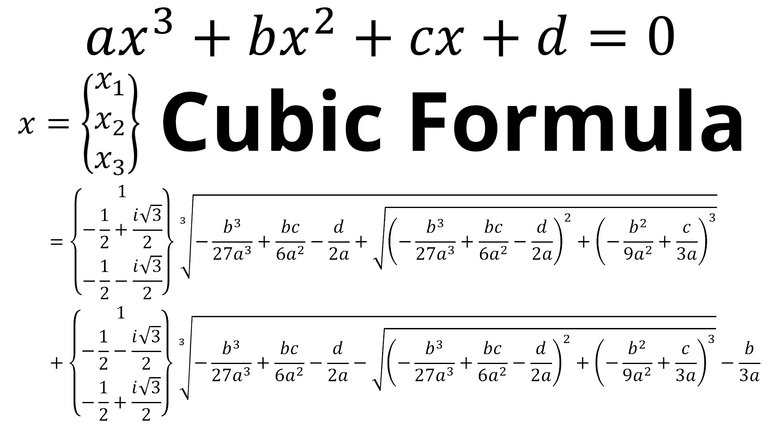
Recap on the Quadratic Formula
Recall my earlier video on the Quadratic Formula:
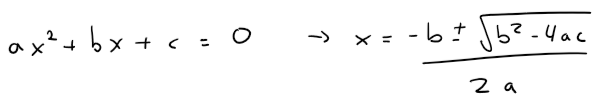
In that video I derived it by Completing the Square.
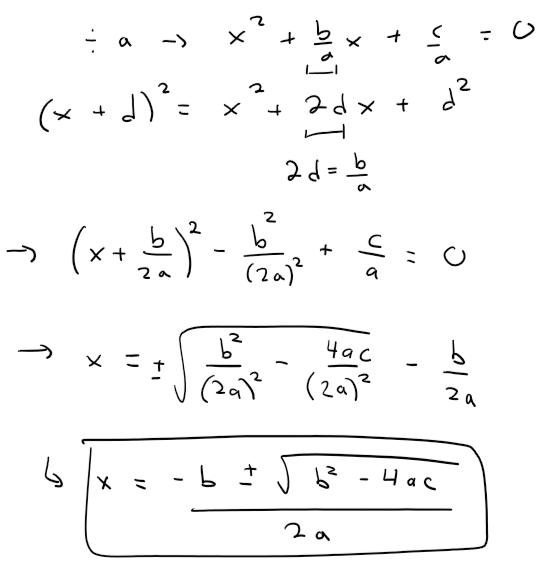
Cubic Formula
The cubic formula is the solution to the cubic equation:
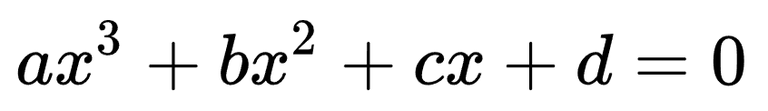
where: a ≠ 0

Derivation of Cubic Formula
I will be following the steps done by blackpenredpen's derivation.
Step 0: Solve Quadratic Formula using the PQ Substitution Method
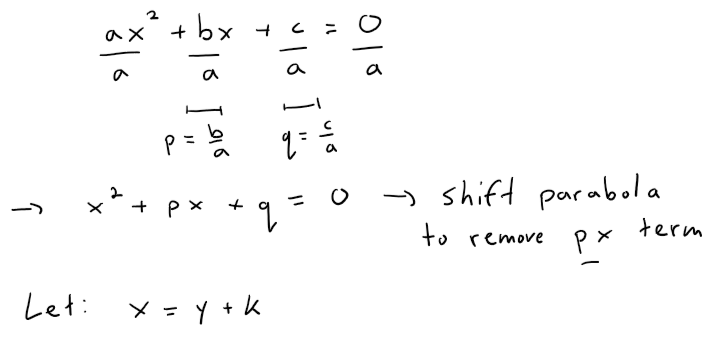
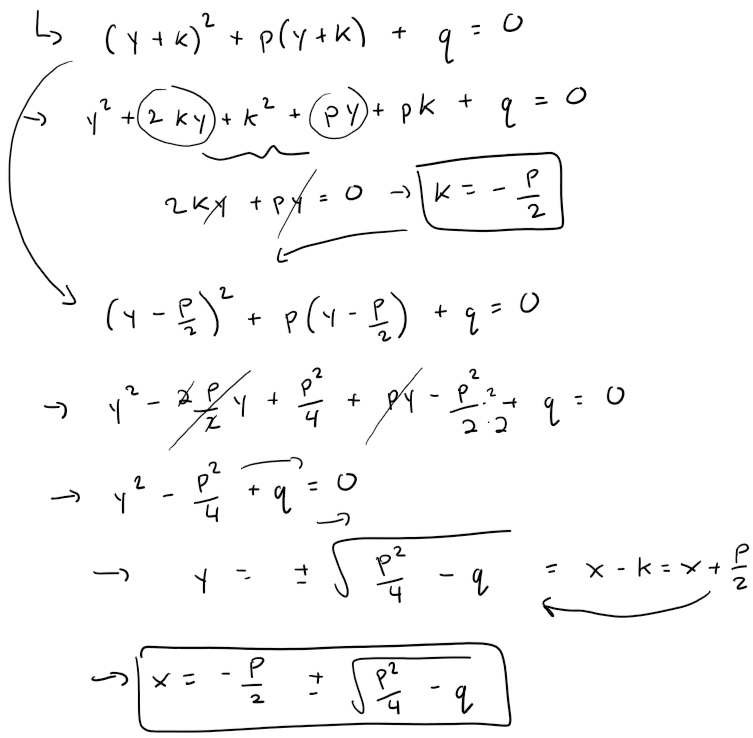
Step 1: Get rid of x2 term using PQ Substitution
Just as in the PQ substitution method for the quadratic equation, we would like to get rid of the x2 term from the cubic function:
ax3 + bx2 + cx + d = 0
It's possible to solve the equation y3 + py + q = 0 by applying Vieta's substitution to obtain a quadratic formula:
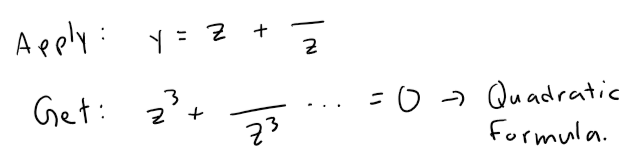
Let's now apply the PQ substitution method to the cubic function.


Step 2: Solve y3 + py + q = 0 using Vieta's Substitution
Now we can apply Vieta's substitution to transform our PQ cubic equation into a quadratic equation.
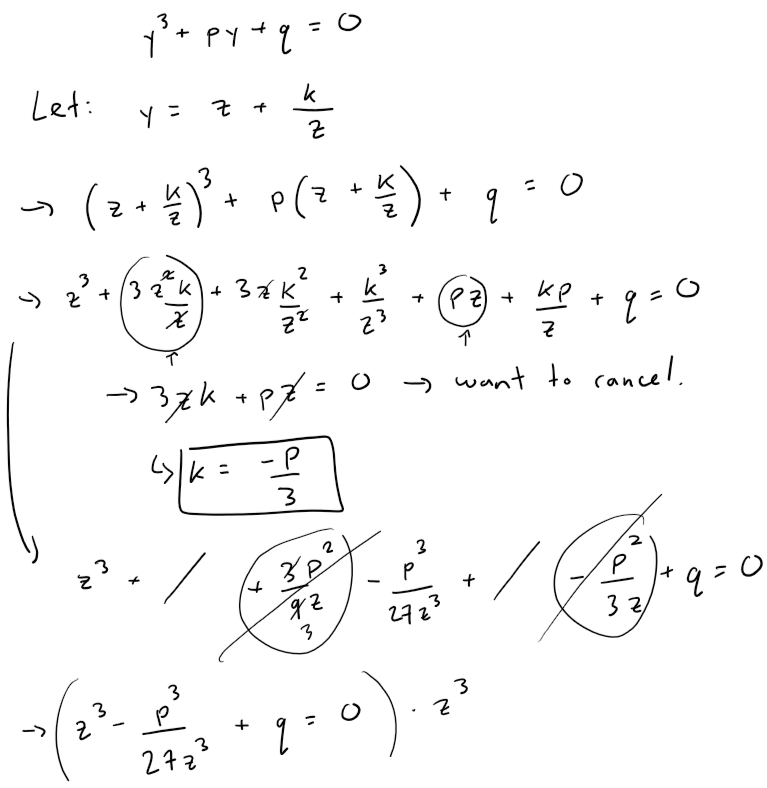
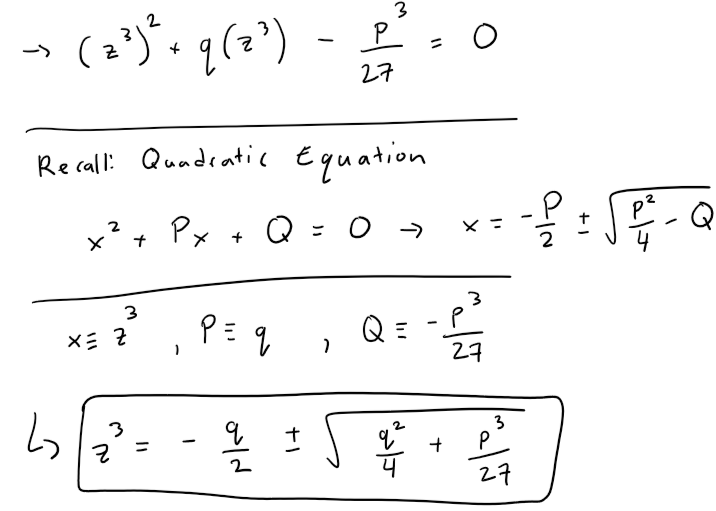
Step 3: Find First Solution
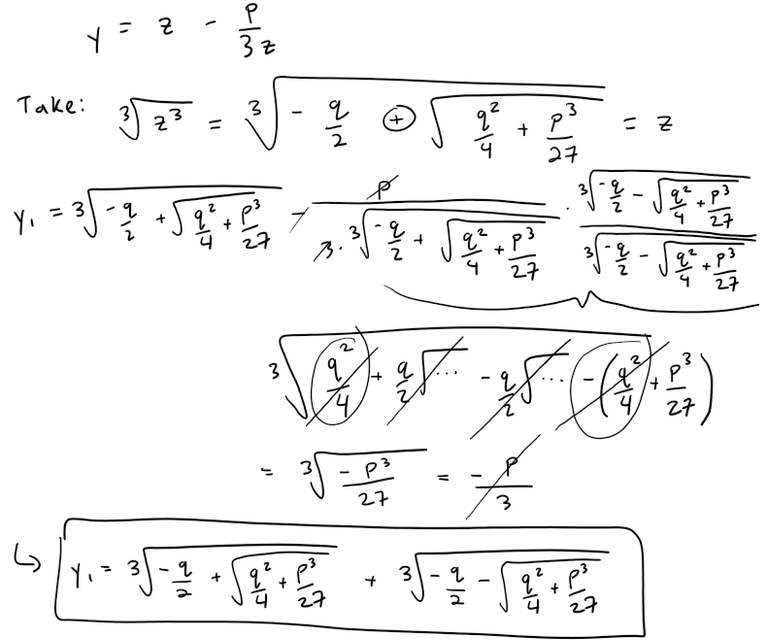
Note that if we plugged in the negative version of the Vieta quadratic formula, we would just get the positive conjugate, and hence the same solution.
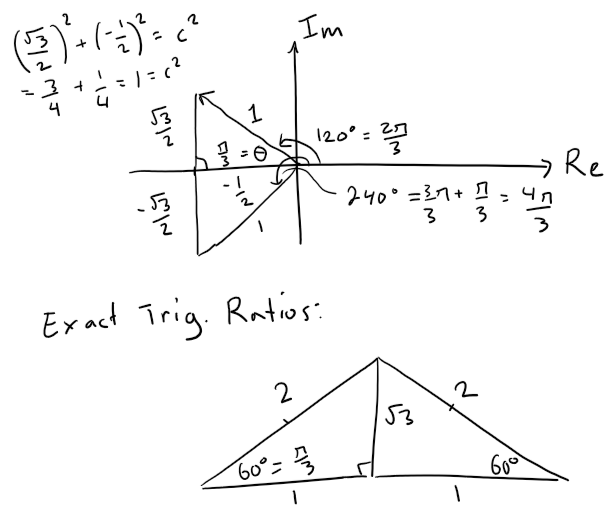
Step 4.1: Cube Root of Unity
The cube root gives 3 solutions just as the square root gives 2 solutions.
We can find these solutions by factoring the square and cube root of unity via difference of squares and difference of cubes formula, respectively.
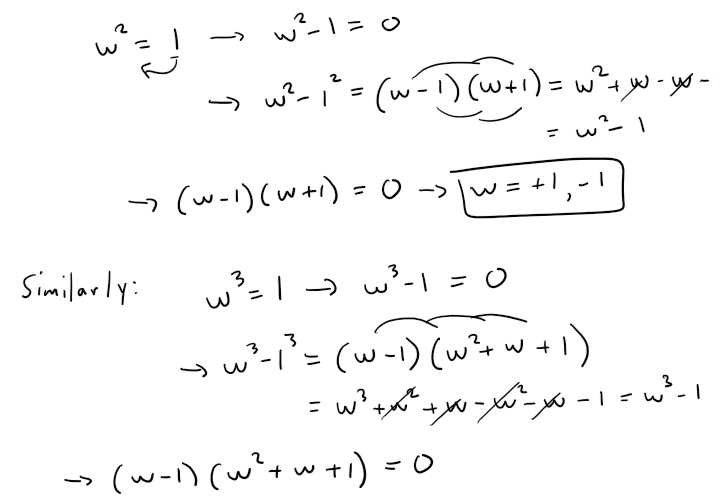
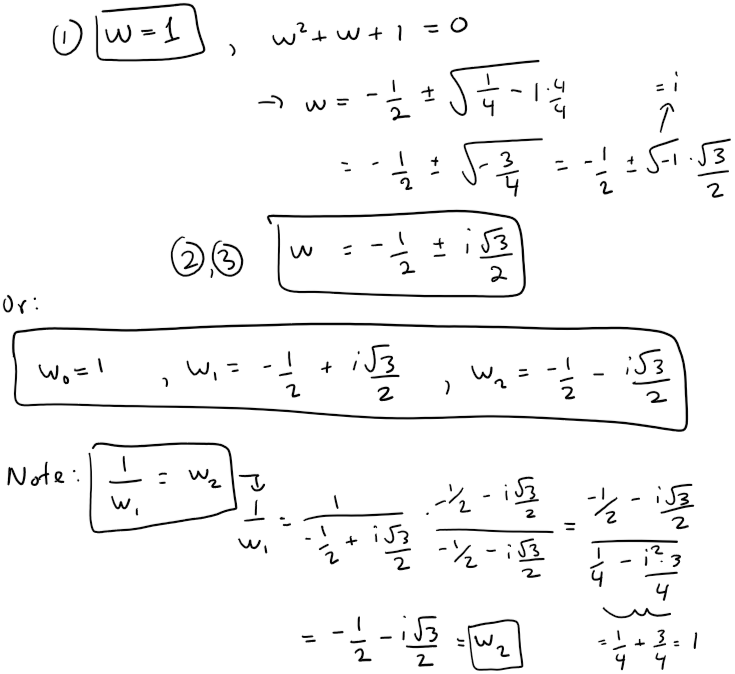
Note also that these complex factors are just rotations in the complex plane:
Step 4.2: Find the other Solutions for y
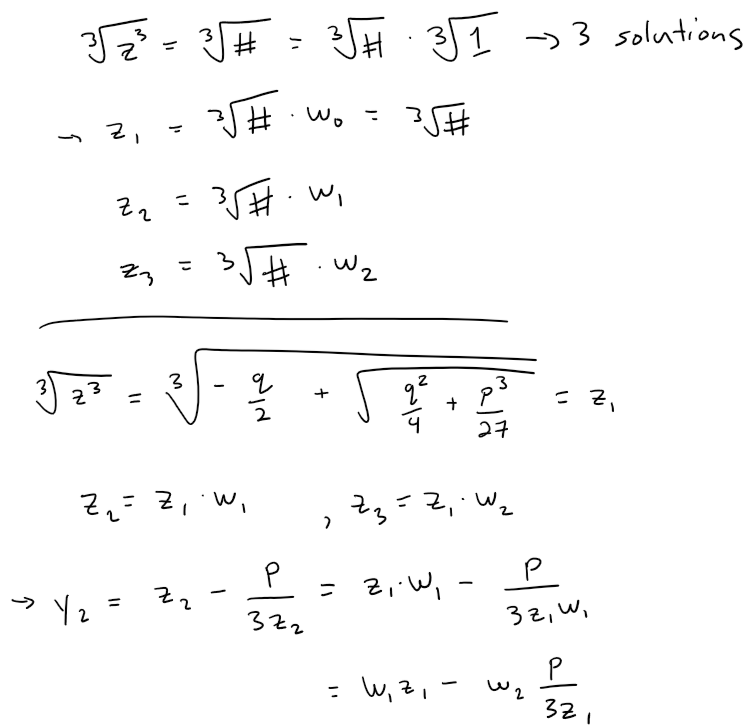

Step 5: Put Everything Together
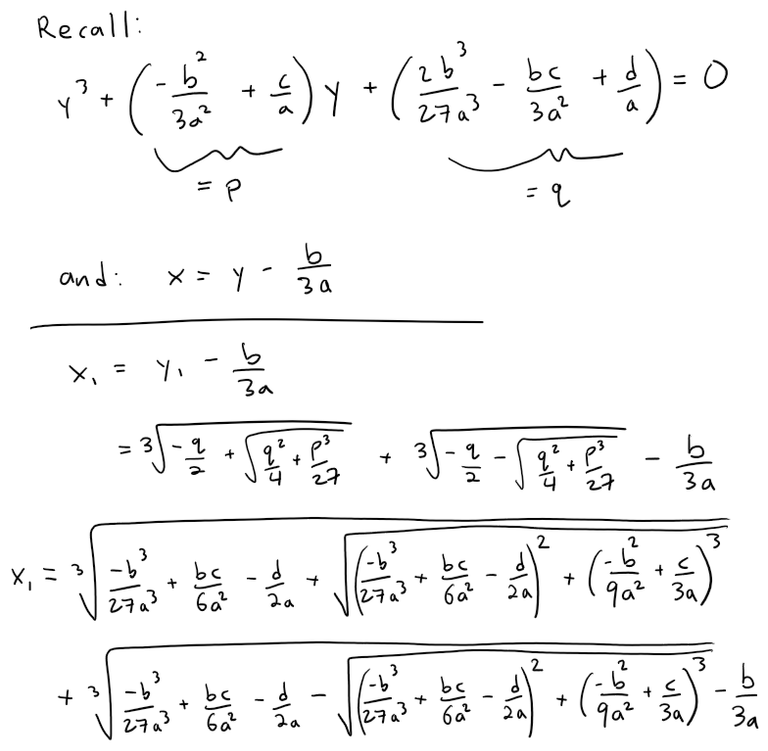
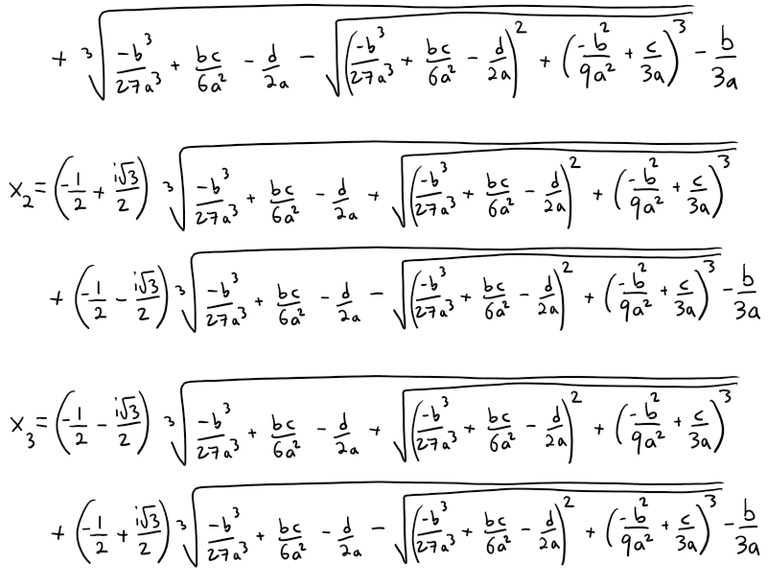
Double check:

The rewards earned on this comment will go directly to the people( @tsnaks ) sharing the post on Reddit as long as they are registered with @poshtoken. Sign up at https://hiveposh.com. Otherwise, rewards go to the author of the blog post.
!summarize
Part 1/7:
Understanding the Cubic Formula and its Proof
In this longform article, we'll delve into the cubic formula, its proof, and how it relates to the earlier quadratic formula. This exploration will elucidate the complexities of cubic equations and show how mathematical techniques can be applied to derive solutions systematically.
Overview of the Quadratic Formula
Before we address cubic equations, it’s important to recap the quadratic formula, which is a well-known equation of the form ( ax^2 + bx + c = 0 ). The solutions for ( x ) can be derived using the formula:
[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
]
Part 2/7:
The proof of this formula involves completing the square, a method where the quadratic is manipulated into a form that highlights its roots. This derivation lays the groundwork for understanding the more complex cubic formula that we will discuss.
The Cubic Equation and Its Solutions
The cubic formula deals with equations of the form:
[
ax^3 + bx^2 + cx + d = 0
]
where ( a \neq 0 ). Unlike the quadratic formula, cubic equations can have up to three real solutions. The cubic formula offers a method to find these solutions, represented as:
[
x = \sqrt[3]{-\frac{b}{3a} + \sqrt[3]{\left( \frac{b^2 - 3ac}{3a^2} \right)^2 + \frac{d}{a}}} + \sqrt[3]{-\frac{b}{3a} - \sqrt[3]{\left( \frac{b^2 - 3ac}{3a^2} \right)^2 + \frac{d}{a}}}
]
Part 3/7:
The challenge lies in the complexity of this formula, which combines both real and complex numbers, depending on the discriminant of the cubic equation.
Derivation of the Cubic Formula
To establish the cubic formula's proof, we begin with a substitution method akin to the completion of squares used in the quadratic case. The cubic equation can be simplified by removing the ( x^2 ) term through a transformation ( x = y - \frac{b}{3a} ), leading to a new function where we can apply the PQ substitution method.
Next, we transform the cubic equation into a simplified form that can be solved as a quadratic equation. This uses a form ( y^3 + py + q = 0 ), which allows us to focus solely on the cubic roots without the complexity of the quadratic term.
Part 4/7:
After manipulating the polynomial into this form, we utilize a Vieta substitution, returning to our roots using:
[
v = y + \frac{p}{3}
]
Identifying Roots Through Cubic Unity
One crucial aspect of finding solutions involves understanding the cube roots of unity, which relate to the geometric properties of complex numbers. These roots are essential for calculating the distinct solutions of cubic equations, as they signify the angles in the complex plane where the roots will lie. The three cube roots of unity are:
( 1 )
( \frac{-1 + \sqrt{3} i}{2} )
( \frac{-1 - \sqrt{3} i}{2} )
These correspond to rotations in the complex plane and play an integral role in the cubic equation's solutions.
Solutions Derived from Cube Roots
Part 5/7:
When deriving the solutions ( y_1, y_2, ) and ( y_3 ), we incorporate these cube roots of unity to illustrate how the cubic equation can manifest different roots through varying formulations. The general solutions thus become complex due to the presence of imaginary numbers.
The patterns emerge through utilizing a combination of the principal root derived earlier and the square root values influenced by the coefficients of the original equation. Each solution corresponds uniquely to the specific cube roots.
Final Consolidation of Findings
Part 6/7:
Ultimately, the key to solving cubic equations lies in the meticulous application of algebraic identities, understanding complex numbers' geometry, and employing innovative substitution methods. Each derived solution aligns with the original equations while embracing the complexities introduced through real and imaginary interactions.
In summary, both the quadratic and cubic formulas present fascinating insights into how algebra operates within differing polynomial degrees. The derivation, application, and utility of these formulas showcase the beauty of mathematical reasoning and problem-solving.
Part 7/7:
For those interested in a deeper exploration of this mathematical approach, detailed notes are available for download in PDF format, along with video resources and timestamps for structured learning. Engage with these materials to enrich your understanding of cubic equations and their solutions in the realm of advanced mathematics.
You can check out this post and your own profile on the map. Be part of the Worldmappin Community and join our Discord Channel to get in touch with other travelers, ask questions or just be updated on our latest features.