Hola, estimados amigos de Hive, espero que tengan un feliz fin de semana. Hoy quiero decirles que mi pasión por la educación es de cuna, mi mamá fue una de las mejores maestras de su grupo, hasta que se jubiló; por otra parte, mis abuelos fueron lectores insaciables. Así que desde siempre mis hermanos yo crecimos entre papeles, lápices, colores, libros y el amor por enseñar y aprender.

Material didáctio realizado para hacer correspondencia entre el número y la cantidad

Recuerdo que desde pequeños jugábamos a ¨la escuelita¨ y me gustaba participar de ambos lados; algunas veces de maestra y otras de estudiante. Nos divertíamos un montón. Así que cuando iba a iniciar el bachillerato, mi decisión por las humanidades y luego por una carrera universitaria de educación, fue una crónica de muerte anunciada, o mejor dicho, fue amor a primera vista.

Así que hoy este post es sobre un tema educativo, les voy a hablar en forma general sobre los trastornos del cálculo y del modelo teórico de triple código, uno de los de mayor acogida en la comunidad científica, que trata de explicar el por qué algunos niños tienen estas limitaciones y dónde se ubican en el proceso de construcción del número y el cálculo matemático.

Material didáctico para comparar números - los iguales -

Además les mostraré algunas actividades, incluidas las que he realizado con los niños que atiendo a nivel psicopedagógico que presentan dificultades con las matemáticas. Demás está decirles que espero que les sea de provecho y que lo disfruten tanto como yo, porque este post me dan la oportunidad de repasar y leer material nuevo, lo cual es muy bueno para el fortalecimiento de mi trabajo docente.

Contrario a lo que sucede en el área de lectura y escritura, donde contamos con modelos teóricos consolidados, aceptados por la comunidad de experto y puesto en práctica por círculos académico, en el área de las matemáticas la investigación está más dispersa, a pesar de que ha habido un denodado esfuerzo por producir teorías que traducidas en modelos explicativos de los trastornos del cálculo, nos brindan un horizonte para orientar nuestro trabajo.

Los trastornos del cálculo.

En el desarrollo, para comprender cuándo algún aspecto del mismo está desviado, hay que partir del proceso ¨normal¨ y toda vez que lo comprendamos, es cuando comenzamos a diferenciar aquellas conquistas ¨no está en su sitio¨, es decir, que difieren en cuanto a edad cronológica. Así, para saber cuándo existe un trastorno específico del cálculo, debemos aplicar instrumentos estandarizados y normalizados, los cuales nos van a indicar la desviación estándar; cuando la media se aleja dos o más desviaciones típicas, podemos hablar de una dificultad específica del cálculo.

Material didáctico realizado para hacer comparaciones entre los números y las cantidades que lo representan.

En el manual de diagnósticos y estadísticas vigente, DSM5, aparece tipificado de la siguiente forma:

…Dificultades para dominar el sentido numérico, los datos numéricos o el cálculo (p. ej., comprende mal los números, su magnitud y sus relaciones; cuenta con los dedos para sumar números de un solo dígito en lugar de recordar la operación matemática como hacen sus iguales; se pierde en el cálculo aritmético y puede intercambiar los procedimientos).
Dificultades con el razonamiento matemático (p. ej., tiene gran dificultad para aplicar los conceptos, hechos u operaciones matemáticas para resolver problemas cuantitativos).
…Con dificultad matemática:
Sentido de los números
Memorización de operaciones aritméticas
Cálculo correcto o fluido
Razonamiento matemático correcto
Trastorno específico del aprendizaje: DSM 5 Y CIE-10

El modelo del triple código.

Es la teoría propuesta por Stanislas Dehaene, un neurocientífico cognitivo, de origen francés que ha investigado la cognición numérica, entre otros aspectos y temas vinculados con las bases neurobiológicas. Dehaene afirma que afirma que la causa del trastorno de cálculo está en el sentido del número.

El sentido del número es una capacidad cognitiva para representar cantidades, que todos tenemos al nacer; pero son cálculos que se realizan con cualquier objeto, no necesariamente tiene que ser con números arábigos. Estas cantidades son continuas, luego se dividen en representaciones analógicas, primer módulo del modelo.

Pero no es sólo esto; es necesario que haya correspondencia entre el número en cuestión y la cadena de palabras que definen la cantidad del mismo. Si se logra llevar a término este proceso: relacionar los conceptos con los dígitos, es cuando podemos hablar del sentido de número.

Material didáctico realizado para hacer múltiples actividades con los números del 1 al 60: series, comparaciones, conteo, intérvalos, entre otros.

El procesamiento de los números.

Comprender el procesamiento de los números es un aspecto central, primero para conocer el proceso de construcción estándar, o ¨normal¨, que recorre el desarrollo; y luego para poder establecer la desviaciones, si las hubiera.

Cuando el niño es pequeño, antes de adquirir el lenguaje, procesa los números en forma no-simbólica. Puede distinguir un grupo de objetos menores a 4 elementos, también entre grupos muy grandes y muy pequeños; es decir, conjuntos con notables diferencias observables. A este nivel, priva el sistema perceptivo-visual.

Posteriormente, durante el desarrollo, el sistema numérico pre-verbal deriva al sistema numérico verbal; el cual el niño construye con el lenguaje en interacción con su medio ambiente, en forma paralela al código arábigo: la categoría simbólica.

Módulos de procesamiento numérico: modelo del triple código

El primer módulo que describe Dehaene es el Analógico. En el mismo deben desarrollarse competencias cognitivas que el niño construye a partir de un repertorio innato. Entre ellas:

La línea numérica.

Conocida también como recta real, es una línea donde se pueden representar lo números separados por una distancia fija.

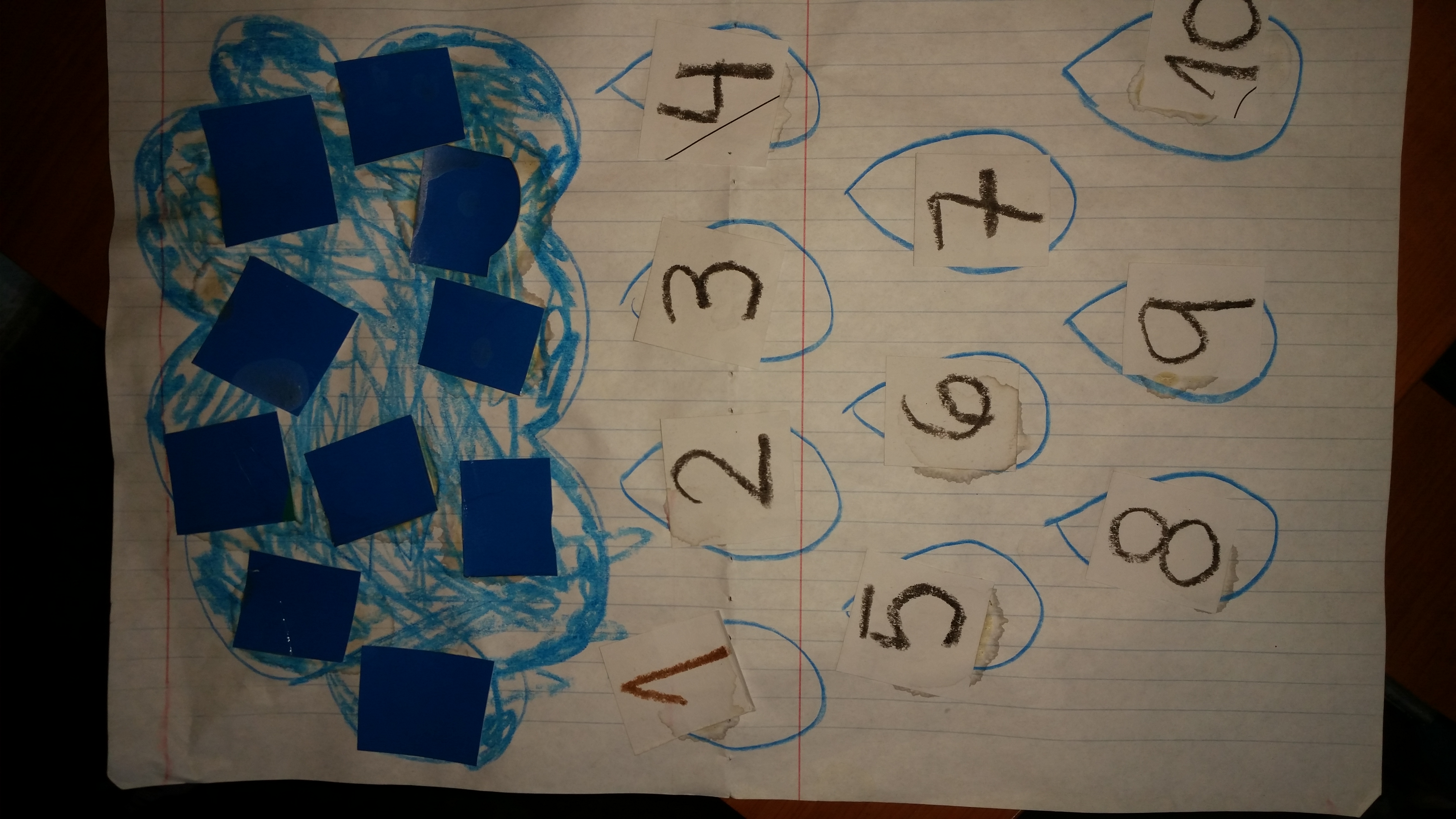
Línea numérica, de intérvalos iguales.

Efecto de distancia y tamaño.

Son conceptos fundamentales en la teoría de Dehaene. El efecto de la distancia se observa cuando la persona se toma mayor tiempo para comparar dos números, por ejemplo:

…se observa de manera sistemática que lleva más tiempo decidir que 71 es más grande que 65, que la misma decisión entre 79 y 65.
El acceso interno a la cantidad parece ser un paso obligatorio en el procesamiento de número, porque un efecto de distancia se encuentra incluso cuando los sujetos sólo tienen que decir si dos dígitos son iguales o diferentes (Dehaene y Akhavein, 1995)
Evaluación de los módulos de codificación numérica en niños con trastorno del cálculo

Selecciona en cada caso el número mayor.

Efecto de tamaño.

Se hace referencia a que para la persona es más difícil hacer la discriminación de los números, con igual distancia numérica, en tanto aumenta sus valores. Por ejemplo, en una actividad de comparación se tomará más tiempo y posiblemente habrá más respuestas erróneas para decidir entre el par 12 y 13 que entre el par 4 y 5.

Actividad de suma para la comparación de resultados.

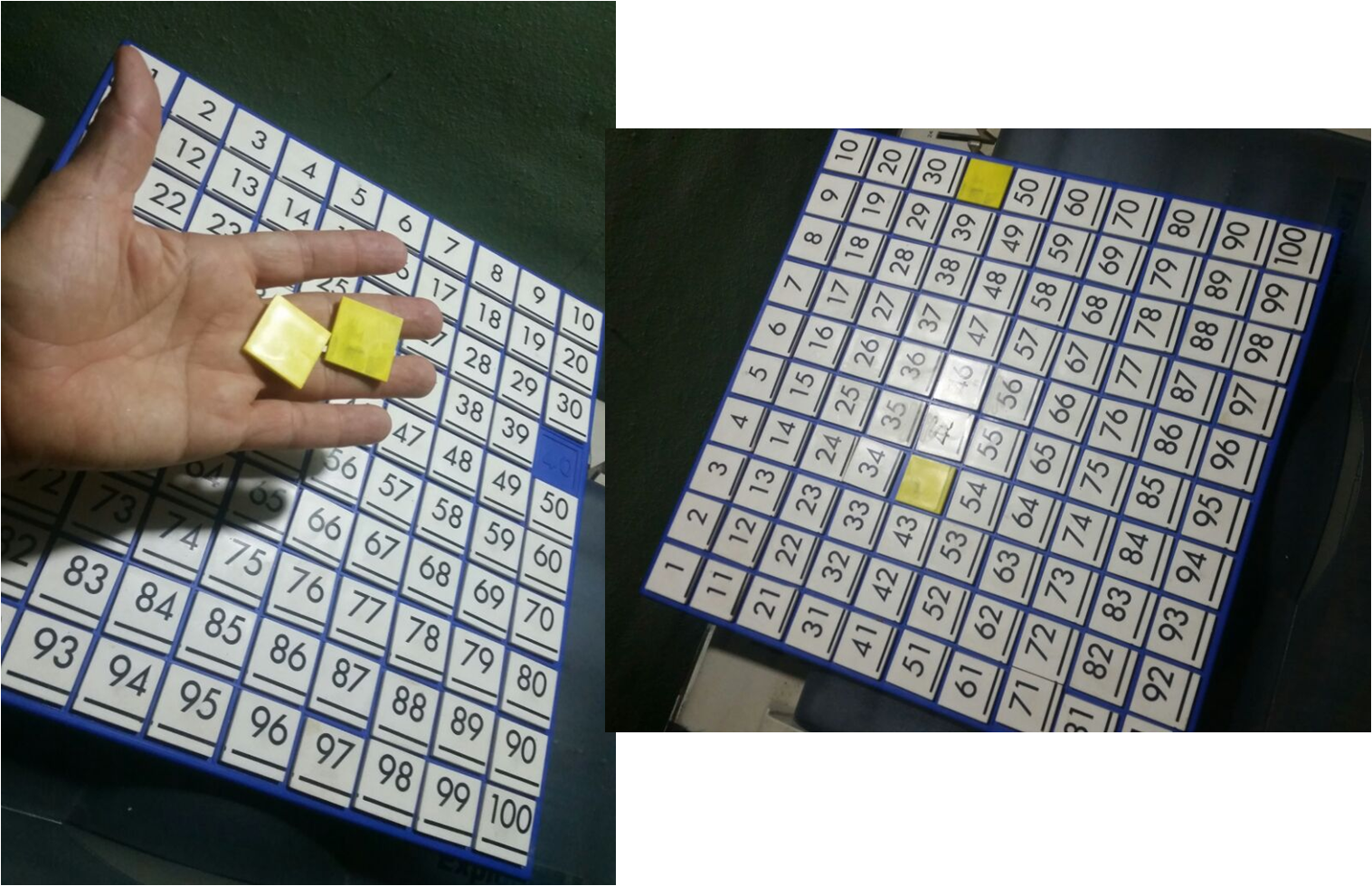
Tablero para trabajar los efectos de distancia y de tamaño entre los números (1-100).

Subitización.

Consiste en reorganizar súbitamente un número de objetos y poder saber cuántos, son sin necesidad de contarlos, es como un mecanismo global. En niños pequeños la subitización se hace hasta cuatro elementos. Es decir, es la capacidad de reconocer en forma instantánea la cantidad de elementos de un conjunto, sin necesidad de apoyare en las técnicas de conteo.

Tarjetas para identificar cantidades, sin necesidad de contar.

Cálculos aproximados por comparaciones.

Son estimaciones, que es una competencia importante del pensamiento matemático, no es adivinación porque está soportada tanto en la lógica como en la intuición.

La importancia que esta estrategia de pensamiento tiene para resolver problemas de la vida cotidiana y de las ciencias, donde si bien es necesario razonamientos correctos en la generalidad de los casos son suficiente resultados aproximados…
La estimación, una forma importante de pensar en matemática

Actividades para la estimulación las comparaciones por aproximaciones y el pensamiento intuitivo.
Imagen realiza en el programa Power Point.

La fracción de Weber.

Es un aporte muy importante en el estudio de la percepción y dice que hay un umbral en el que podemos percibir un cambio de magnitud en los estímulos.

Para entender mejor la Ley de Weber-Fechner, vamos a ilustrarlo con un ejemplo: si sostenemos en la mano una pelota de 100 gramos, tal vez no la podamos distinguir de otra de 105 gramos, pero sí de una de 110 gramos. En este caso, el umbral para discernir el cambio de masa es de 10 gramos.
La Ley de Weber-Fechner: qué es y qué explica

Material didáctico para organizar por tamaños y hacer comparaciones.

Módulo visual a rábigo.

Es la representación del número arábigo. En este módulo se maneja y contiene la representación visual del símbolo de los números naturales, que nos indica la cantidad contenida en cada marca gráfica o número, en forma progresiva viso-espacial, como una lista organizada secuencialmente.

Se codifican los numerales en notación arábiga y se utiliza principalmente para realizar operaciones de cálculo de varios dígitos escritos y que requieren una precisión. Dehaene propone que existen dos vías para la lectura de números en forma verbal y en forma arábiga

Ruta superficial: basada en la aplicación de los correspondientes algoritmos de conversión.
Ruta semántica profunda: funciona a través de la ruta léxica, … sólo con números familiares o significativos que han desarrollado una entrada léxica específica (Dehaene, 1997)
Evaluación de los módulos de codificación numérica en niños con trastorno del cálculo

Representación de números arábigos en forma progresiva viso-espacial.

Representación de números en forma no progresiva.

Módulo Verbal

Es propiamente la lectura del número y de las cantidades, la pronunciación. En este módulo se maneja el código auditivo-verbal para todas aquellas tareas relacionadas con la codificación de la estructura verbal de la palabra del Número.

Es decir, todo lo que comprende la sintaxis correcta, el orden de las palabras, para leer y explicar un problema matemático, por ejemplo, leer dos cantidades, leer signos de suma o resta, entre otros.

Actividad para colocar el nombre a los números.

Hasta aquí he completado algunos ejemplos de las actividades que ilustran los módulos del modelo del triple código. Lo que se espera es rescatar el sentido del número para estimular el pensamiento lógico-matemático en las diferentes etapas de este modelo.

Espero que te haya sido de utilidad, que puedas comentar y compartir con otras personas interesadas en el tema desde lo personal y/o profesional.

¡Gracias por la visita!

Referencias.

Stanislas Dehaene.

Evaluación de los módulos de codificación numérica en niños con trastorno del cálculo.

Evaluación de los módulos de codificación numérica en niños con trastorno del cálculo.

La estimación, una forma importante de pensar en matemática

La Ley de Weber-Fechner: qué es y qué explica.

Trastorno específico del aprendizaje: DSM 5 Y CIE-10.

Todas las fotos fueron tomadas por mí, con el teléfono Samsung S5 y editadas en el programa Power Point.