Hello friends of steemit, this is my first publication on mathematics and today I want to start with a post talking about the circumference, a geometric figure associated with analytical geometry, I will also explain with some images how is the mathematical procedure for each case of this figure, applying the algebraic properties we can observe how the geometric exercises are solved in an easy and simple way. I invite you to observe this interesting post.
The circumference is a particular limiting case of the ellipse in which the two axes coincide in size.
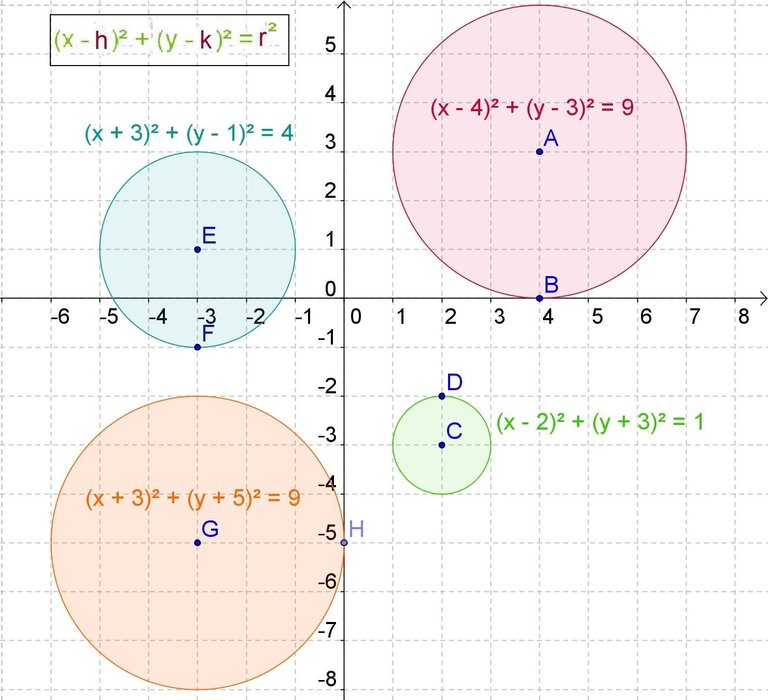
In the drawing we can see two circles with their corresponding equations, the magenta circle has the center at the origin of coordinates (0,0) while the green circle has it at the point (2,6).
Since both circles have in the second member of their ordinary equation the number 25, which is five squared, this means that this is the radius of the circumference.
The equation of the circumference will always be the binomial formed by x minus the length of the center to the y axis, all of it squared, added to another binomial to the square that consists of the variable minus the distance from the center to the x axis.
The sum of both binomials squared is always equal to radius squared.
The circumference when it is in the origin of coordinates, we have that it is a particular case of the previous one in which to each of the binomies we must subtract the length or distance from the center to the origin of coordinates in both axes, and as this is zero we have that the equation of the circumference that passes through the origin of coordinates is always the sum of the variables squared and equated to the radius squared.
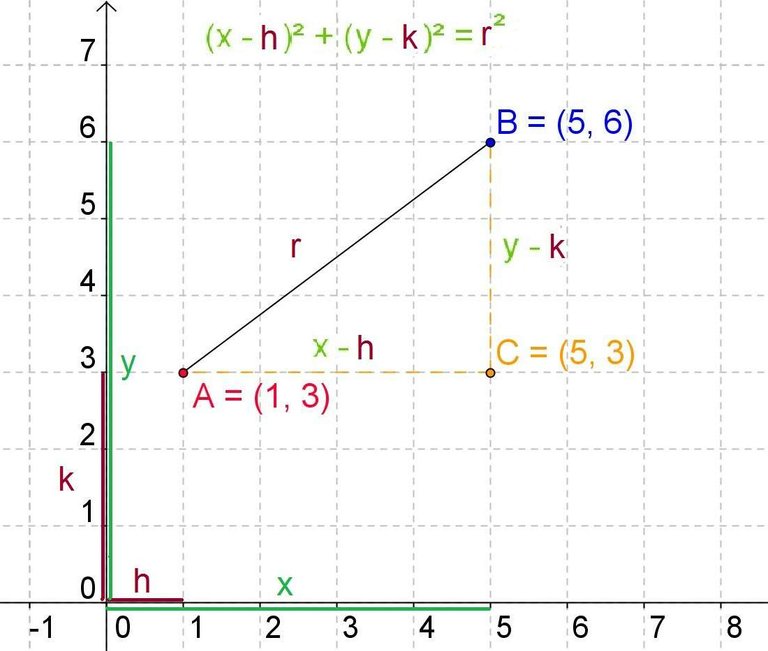
To deduce the equation of the circumference we must take into consideration the concept of distance in analytical geometry. If we want to calculate the distance between two points AB to determine the radius of a circle, we have to think about its lengths or projections on both coordinate axes. The length on the horizontal axis is determined by the coordinates in x, in this case 5 - 1 equal to four, (x-h).
The coordinates on the y-axis are also the difference of one point minus the other, in this case it is 6 - 3, whose difference is three, (y-k).
We already have the legs of a right triangle whose hypotenuse will later be the radius of the circumference. Consequently, since the hypotenuse squared equals the sum of squared squares, the radius or hypotenuse of the right triangle squared equals the sum of both squared squares, (xh) plus (yk), and this is the length of the radius in the equation of the circumference, where point A is going to be the center of the circumference and point B is going to be a moving element that is always the same length from the center.
The center of the circle will be determined by the coordinates of A.
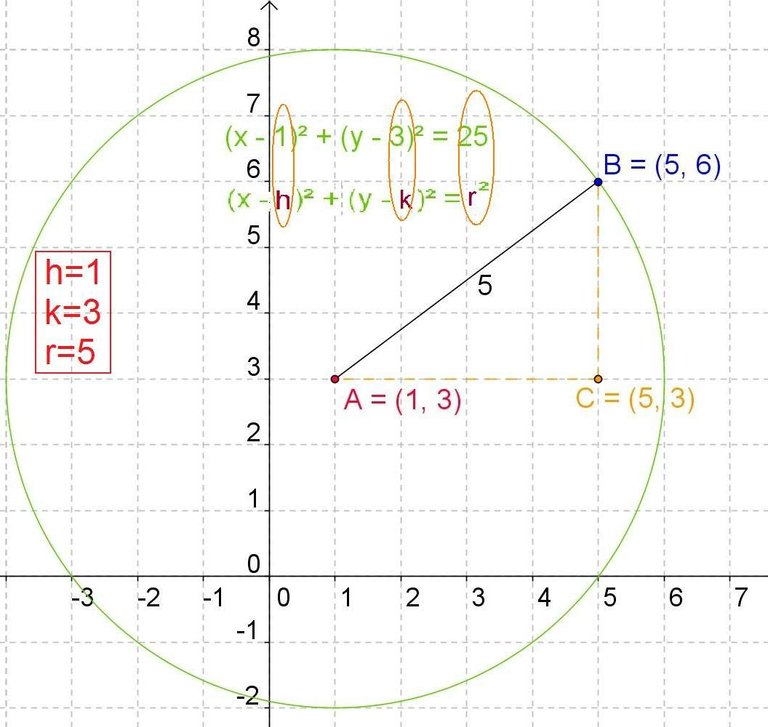
In this drawing we are given as data the equation of the circumference and we must calculate its graph. We have that the hypotenuse squared is equal to the sum of squared squares, so the radius squared will be equal to 25 and the radius equal to five.
To determine the coordinates of the center, as we know that in the equation of the circumference we have the first binomial squared from which the length in x is subtracted from the distance of the center of the circle the origin, therefore h = 1.
We also have that in the second binomial squared the length in y from the location of the center to the origin is subtracted, therefore k = 3.
Having then the coordinates of the center (1,3) and having the radius of the circumference (five) we can already draw the circumference and its position with respect to the Cartesian axes.
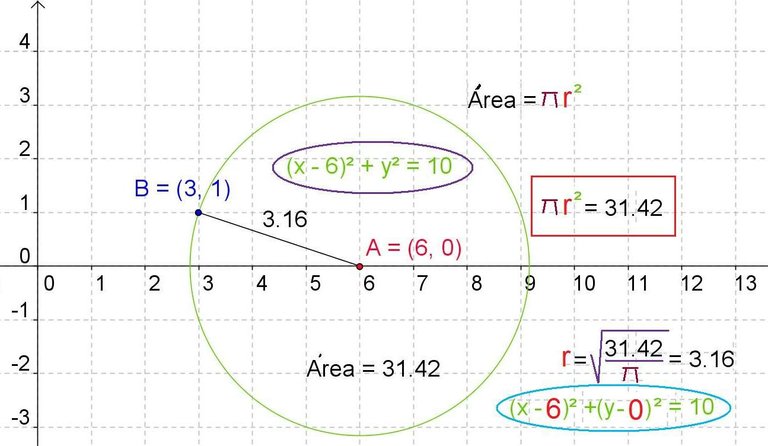
In this exercise we have as data the area of the circle (31,42) and the center that is the point of coordinates (6,0) and they ask us to calculate the equation of the circumference.
Since the area of the circumference is pi by the radius squared, 31.42 is equal to pi by the radius squared. Clearing the radius we have that is equal to 3.16.
The equation of the circumference will be the binomial (x-6) squared (x minus the coordinate in x of the center) plus (y-0), (and minus the y-coordinate of the center of the circle) squared.
The sum of both binomials squared will be equal to 3.16 squared which is 10.
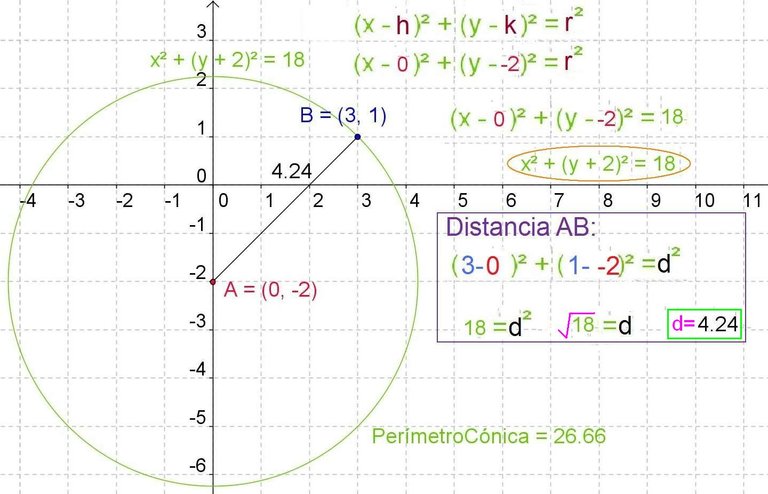
To calculate the equation of the circumference given the center (0, -2) and an outer point (3.1), we substitute the two parameters of the center in the equation, these being respectively h and k ..
To obtain the dimension of the radius -operation framed in the rectangle-, we use the Pythagorean theorem generated by the formula: coordinate in x of a minus point co-ordinated in x of the other point, all in parentheses and squared. We do the same with the coordinates of the y-axis, we apply the difference of both and we raise the square binomial. The sum of both binomials squared must be equal to radius squared. In this way we have the magnitude 18 that is equal to the distance or radius squared, hence the distance between the point and the center is the square root of 18, that is, 4.24.
We substitute this magnitude in the formula and we already have the equation of the circumference (it appears in the drawing framed in a red ellipse).
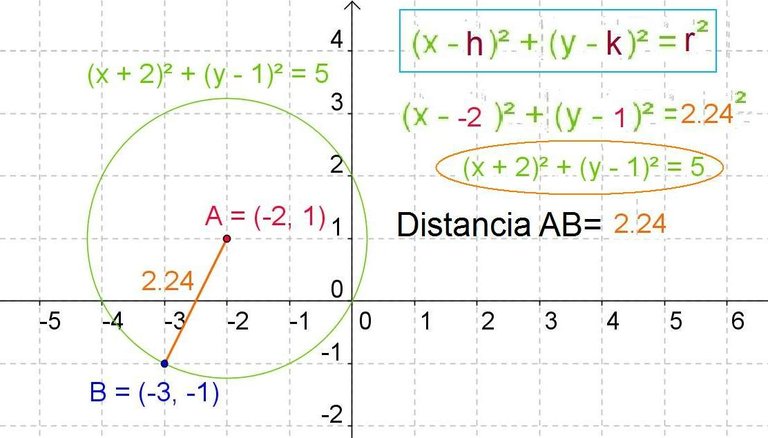
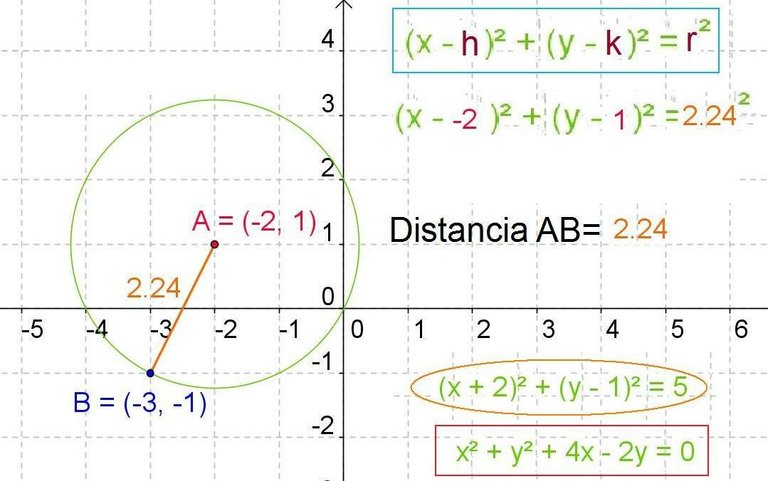
Bibliography :
- https://en.wikipedia.org/wiki/Analytic_geometry
- https://www.khanacademy.org/math/geometry-home/analytic-geometry-topic
- http://djm.cc/library/Analytic_Geometry_Siceloff_Wentworth_Smith_edited.pdf
- geometry analytic circumferences.2010. marco rubio, maria fernandez.
- Analysis of the geometrical figures, analytical geometry .2010 tereza D. LUISANNA T.
Its a very post @theprinc. I suggest you do a better image sourcing to get a favour from #steemstem.
Being A SteemStem Member