综 述
极值原理是最小二乘回归的理论基础,因为最小二乘回归是最重要的数据处理工具,也是试验设计的理论基础,研究优化论必须了解极值原理。为以后叙述和应用方便,这里引述一些有关资料,个别地方作了引伸。 受 HTML 语言的限制,符号不够规范,请查各种数学分析教程。
1. 函数的极值原理
1.1 单变量函数的极值
若函数 f(x) 在点x0 的双侧邻域中有定义,对于|x-x0|<δ 内的一切点 x, 都有
若函数 f(x) 在 x0处不可微,x0也可能是极点。因此,极值存在的必要条件应该是使 f'(x)=0 或 f'(x) 不存在的地方。
1.1.1 极值存在的充分条件
极值存在的充分条件归纳为以下三种判别法:
第一判别法
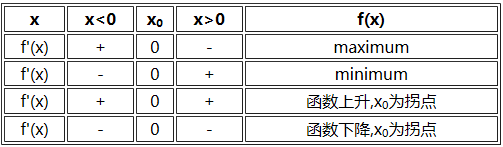
第二判别法
若函数 f(x) 在邻域 |x-x0|<δ内有二阶导数 f''(x),并且在 x0 处有
第三判别法
若函数 f(x) 在邻域 |x-x0|<δ 内有各阶导数 f(n)(x),并且在x0处有
若 n 为偶数,则函数 f(x) 在点 x0处有极值
若 n 为奇数,则函数 f(x) 在点x0处无极值。
1.1.2 函数的最大值和最小值
函数的最大值和最小值是指 f(x) 在 [a,b] 上的最大值和最小值,函数在 [a,b] 上的最大值和最小值一定存在。其求得步骤为:
求出 (a,b) 内 f'(x) 的全部零点和不存在点xi,并分别计算出f(xi);
计算出 f(x) 在 [a,b] 的两个端点上的值 f(a),f(b);
比较之,得到最大值和最小值。相应于取最大值和最小值的点(位置)为函数 f(x) 在 [a,b] 上取最大值和最小值的点,有时简称峰点。
2. 多元函数的极值
设函数
2.1 多元函数极值存在的必要条件
与一元函数类似,若函数 f(X) 在X0(∈D) 处有极值,则必须
2.2 多元函数极值存在的充分条件
设 X0为函数 f(X) 的一个稳定点,且 f(X) 在 X0的邻域内有定义,连续,有直到二阶的连续偏导数。记 i 阶矩阵为
3. 二元函数的极值
设函数 f(x,y) 在点 (a,b) 的邻域中有定义,连续,且有一阶及二阶连续偏导数。 把多元函数的结果移过来,二元函数在某处 (a,b) 存在极值的必要条件是,在该处函数对 x,y 的一阶偏导数为 0,或不存在。 如果 f(x,y) 对 x 和 y 的二阶偏导数
∂2f/∂x2>0 时,点(a,b)是一个极小点;
∂2f/∂x2<0 时,点(a,b)是一个极大点。
如果Δ<0,点 (a,b) 不是一个极值点。
如果 Δ=0,稳定点 (a,b) 为可疑情形,需另作研究。
4. 研究二元函数的一个特例
注意,析因模型没有表达因子的平方的项,所有二阶析因模型都不含平方项,它们的极值如果存在必不是所研究区域的内点。 换句话说,析因模型的极值点不在区域内部。
参 考
(苏)斯米尔诺夫 著 《高等数学教程》
Congratulations @shenzehe! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!