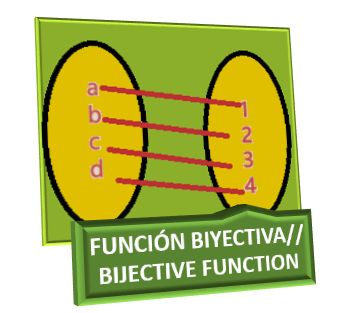
Funciones Biyectivas
Es bueno aclarar antes de comenzar, que debemos tener en cuenta cuáles son: el conjunto de partida y el conjunto de llegada de la función que vamos a considerar, en nuestro caso, vamos a tratar con funciones cuyo conjunto de partida y de llegada es R.
Bijective Functions
 |
|---|
¿Entonces, que es inyectividad?
Una función se dice que es inyectiva si a cada par de elementos diferentes x1 y x2 del dominio de dicha función se le hace corresponder dos imágenes diferentes y1 y y2 en su recorrido.
So, what is injectivity?
A function is said to be injective if each pair of different elements x1 and x2 in the domain of that function is matched by two different images y1 y y2 in its path.
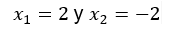 |
|---|
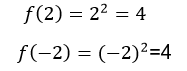 |
|---|
Pero, vamos a demostrarlo:
But, let's prove it:
Let us take any two values in the domain of f:x1 and x2 such that x1 ≠ x2 , and prove that f is not injective.
Comencemos:
Let's get started:
We will proceed by reductio ad absurdum, we will assume a hypothesis that we consider true and then we arrive at the contradiction of the hypothesis.
Sabemos por la hipótesis inicial que x1 ≠ x2 entonces x1 - x2≠0, apliquemos la función a ambos miembros de la igualdad: f(x1 - x2) ≠ f(0), esto significa que:
We know from the initial hypothesis that x1 ≠ x2 so x1 - x2≠0, let's apply the function to both members of the equality: f(x1 - x2) ≠ f(0), this means that:
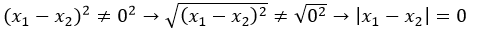 |
|---|
For this equality to be fulfilled it is necessary that:x1 - x2 =0 , from which: x1 = x2
Which contradicts the initial hypothesis where we assumed that: x1 ≠ x2
With this result we can affirm that this function f(x)=x2 is not injective.
Let's see now with this other example:
Probar que la función f(x)=2x-1 es inyectiva.
Prove that the function f(x)=2x-1 is injective.
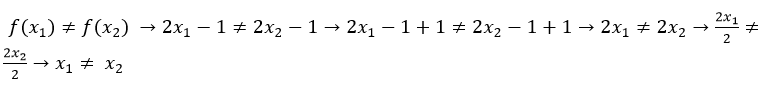 |
|---|
Veamos ahora Función Sobreyectiva
Una función f es sobreyectiva si ∀y ϵ Rec(f) ∃ x ϵ Dom(f) tal que f(x)=y
Let's now see Surjective Function
A function f is surjective if ∀y ϵ Rec(f) ∃ x ϵ Dom(f) such that f(x)=y
Veamos si la función f(x)=x2 es sobreyectiva:
Let's see if the function f(x)=x2 is surjective:
Primero tomaremos y en el Rec(f), eso significa que y=x2≥0, lo cual evidencia que los números reales negativos no pertenecen al recorrido de esta función, en tal sentido existen números reales en el conjunto de llegada que no pertenecen al recorrido de esta función, es por ello que afirmamos que f no es sobreyectiva.
First we will take y in the Rec(f), that means that y=x2≥0, which shows that negative real numbers do not belong to the route of this function, in this sense there are real numbers in the arrival set that do not belong to the route of this function, which is why we affirm that f is not surjective.
But if we redefine it like this:
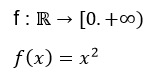 |
|---|
Ejercicio para el lector
Verificar que f(x)=2x-1 es sobreyectiva.
Exercise for the reader
Verify that f(x)=2x-1 is surjective.
Finalmente, cuando una función cumple las dos condiciones anteriores, se dice que es biyectiva. Es decir, una función es biyectiva si y solamente si es inyectiva y sobreyectiva a la vez. En los dos ejemplos anteriores, f(x)=2x-1 es biyectiva y f(x)=x2 no es biyectiva.
Finally, when a function meets the two previous conditions, it is said to be bijective. That is, a function is bijective if and only if it is injective and surjective at the same time. In the two examples above, f(x)=2x-1 is bijective and f(x)=x2 is not bijective.

Créditos
El texto es original de la autora, una de las imágenes es de Pixabay y la otra con la ayuda de Paint.
Credits
The text is original by the author, one of the images is from Pixabay and the other with the help of Paint..
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Congratulations @analealsuarez! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 20000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts: