In the article referring to the study of calculus: the derivative and the tangent line problem, I had the opportunity to make reference to the fact that the derivative is used to calculate slopes, taking into account what I am going to explain in this publication I can argue that the derivative not only provides us with the necessary tools to calculate the slope of the tangent line to a function, but also we can determine the rate of change of one variable with respect to another, which gives the goodness to the derivative of owning a utility in a wide variety of situations, in which speed changes are also found.
The rhythms of changes that our noble nature expresses are infinite in their variety, everything depends on the area of study that these occur, however I can mention some rhythms of changes that tend to occur in different areas of scientific and experimental knowledge, these are:
- Population growth.
- Rhythms of reproduction.
- Fluid flow.
- Speed and acceleration of an object.
Crecimiento poblacional.
Ritmos de reproducción.
Caudal de fluido.
Velocidad y aceleración de un objeto.
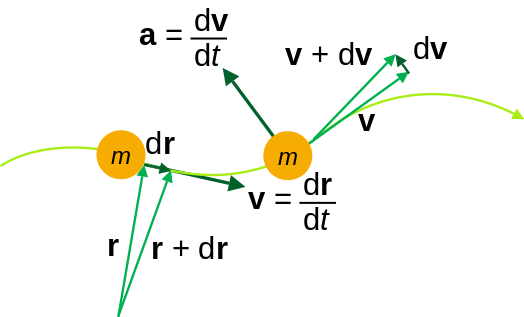
Image source Wikimedia Commons. Public domain
A frequent use of the rhythms of change is to have to describe the type of movement, for example if the movement of the variation is graphed in the Cartesian system and it describes a straight line, then this line is usually represented in a horizontal or vertical position, with a marked origin in it. On such lines, the movement to the right or up is considered positive direction, and the movement to the left or down in the negative direction.
Another characteristic of this phenomenon of change rates is that the function S that represents the position (with respect to the origin) of an object as a function of time t is called position (of) function, in which a certain period of time Δt the object changes its position in a quantity Δs = s (t + Δt) -s (t), so we can use the following formulas:
- Reason = distance / time
- (Change in distance / Change in time) = Δs / Δt, this formula is commonly known as average speed.
Example of average speed of an object in its fall
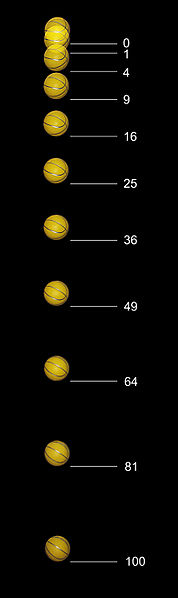
If a baseball is dropped from a height of 100 meters, its height S at time t is represented by the position function
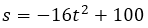
Where s is measured in meters and t in seconds.
The solution of the exercise is to analyze the equation for the calculation of the average speed, if the average velocity is the quotient between the variation of the change of position and the change of time, then we have the average velocity (Δs/Δt) , can be interpreted as follows:
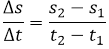
- For the time interval [1,2] it can be said that
= 2 y 
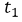= 1.
- To obtain
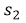y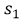 
the value of the time interval in the function is replaced 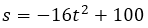, so that:
→ 
→ 
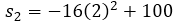
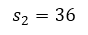
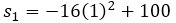
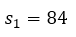
- Having already the variation of time and the variation of the position, we can only substitute in the formula of average speed:
→
→
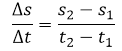
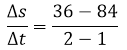
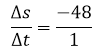
If s is measured in meters and t in seconds then the average speed of the baseball that was dropped from the height of 100 meters in the time interval of [1, 2] seconds carried a speed of 48 meters per second. The fact that the result of the exercise has been negative means that the ball comes down.
For this particular case of the average speed, ie in the specific case that a time interval is known, it is not necessary to use the derivative since the slope can be easily calculated with the formula 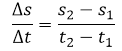, later we will analyze the case of the instantaneous speed, where only one point is known, that is to say at a moment of time, for that particular case if it is necessary to use the use of the derivative.
Application of the derivative for the calculation of the instantaneous velocity
In general if s = s(t) is the position function of an object in rectilinear motion, its velocity at time t is given by the following expression:
= 
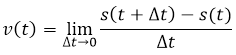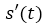
With which we can conclude that the calculation of the instantaneous velocity meets the derivative of the function s(t).
Let's see the following exercise of an application of the derivative for the calculation of the instantaneous velocity:
At the instant t = 0, a projectile is launched from a height of 15 meters. The position of the projectile is given by:
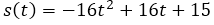
Image source. Wikimedia Commons. Creative Commons License Attribution-Share Alike 3.0 Unported
Find:
to. How long does it take the projectile to reach the ground?
b. What is your speed at the moment of impact?
The solution to this problem is easily solved, we just have to find the derivative of the function .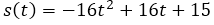
To find the time it takes for the projectile to reach the ground, we equalize the function 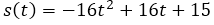to zero, and since the function is of the second degree it will throw us two solutions, a 
. To achieve the speed with which the projectile reached the ground, it is necessary to replace the moment of time of greatest value in the derivative of the function .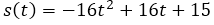
To simplify the derivative of the position function, we perform the derivative by applying the basic derivation rules. So that:
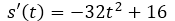
Once the derivative has been obtained, we only need to get the instants of time, for that we take the function 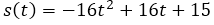and we equal it to zero and find the values of t.
→ 
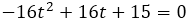
To solve this second degree equation, we apply the equation of the second degree resolvent.
= 
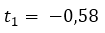
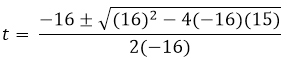
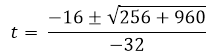
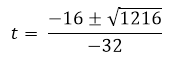
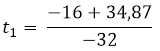
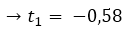
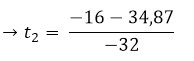
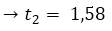
The time it takes the projectile to reach the ground is 1.58 seconds. To find the speed with which I reach the ground it is enough to replace the time of 1.58 seconds in the derivative of the position.
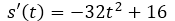
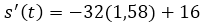
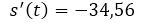
The impact velocity of the projectile with the ground is 34.56 m / s. The negative of the speed means that the object comes down.
Conclusions
In every phenomenon that our nature presents, in which we can appreciate how one variable changes with respect to another, we are in the presence of rhythms or speeds of change, in which the application of the derivative is usually very useful.
More than being able to apply the derivative is very important the interpretation of the functions that govern the behavior of change, since its interpretation will depend on the ease with which we can propose the derivative with which we will find the variation of that rate of change .
In the particular case of this publication we deal with two specific cases, which are the average speed and the instantaneous velocity, although the application of rates of change can be extended even for calculations of flow rate, variation in the viscosity of a fluid , in short for any variable that usually changes with respect to time.
In the case of students at the university level, it is very motivating for them to be able to visualize many of the applications that the derivative has with respect to the phenomenon of the variant of the rhythms or speeds of change.
References consulted
Calculation with analytical geometry. Author: Ron Larson and Robert P. Hostetler. 8th edition. Editorial Mc Graw Hill. Volume I. Mexico 2006.
The calculation. Author: Louis Leithold. 7th edition. Editorial Oxford. Mexico 1998.
"For all that person who is passionate about mathematics, physics, chemistry, biology, education and engineering, I recommend you to take a short step through my publications, I am a person who values intellectual and academic content, always keeping originality in my work. publications, so I recommend all friends of steemit who wish to publish, always respect the rules of steemit, so I invite you not to commit plagiarism in the articles that upload to the steemit platform."
It is very important that it stands out from the way that has been done in this article, other applications that the study of the derivative has different from what is traditionally explained, for example in my case that I study food engineering, I have only seen the part of exercise in what refers to calculation, so I think this point of analysis that you do in this publication seems very important. Congratulations, continue publishing as well, and follow the success @carlos84. Regards