Hi Everyone,

I have decided to revisit game theory. I have made several videos regarding game theory but I have not written that much about it so far. I thought it would be a good idea to explore game theory in a series of posts. I will be looking at some of the fundamental concepts as well as some quite sophisticated concepts, ideas, tactics, and strategies.
What is game theory?
Before I jump into explaining too much. Let’s start by defining game theory. Game theory is the mathematical study of decision-making involving two or more people. Decisions can relate to competition or cooperation. In game theory, decision-makers are referred to as players and the event is referred to as the game. The reward, output, or outcome of the game is referred to as the payout.

How does game theory work?
Games can be described as sequential or simultaneous. Sequential games refer to games that can be observed as if the players are taking turns. Simultaneous games refer to games where players make decisions at the same time. Sequential games allow the second mover (the player that goes second) to observe the actions of the first mover. For simultaneous games, neither player is able to observe the other player until both players have made a decision.

Game theory can be used to study one-off games or repeated games. A one-off game is just played once, while a repeated game can be played a finite or an infinite number of times. The optimal strategies applied for these types of game can vary significantly.
The strategies applied to games with perfect information is different from strategies applied to games with imperfect information. For games with perfect information, optimal strategies can be determined for each player. For games with imperfect information, optimal strategies for each player generally cannot be determined.

Sequential games
In a sequential two player game, there is a first mover and a second mover. The second mover can observe the first mover’s move and therefore can select their optimal outcome. If the first mover knows all the payouts, the first mover can predict what the second mover will do. The first mover will select the action that will provide the highest payout out of the possible selections made by the second mover. The sequential game can be presented in the form of a game tree as shown below.
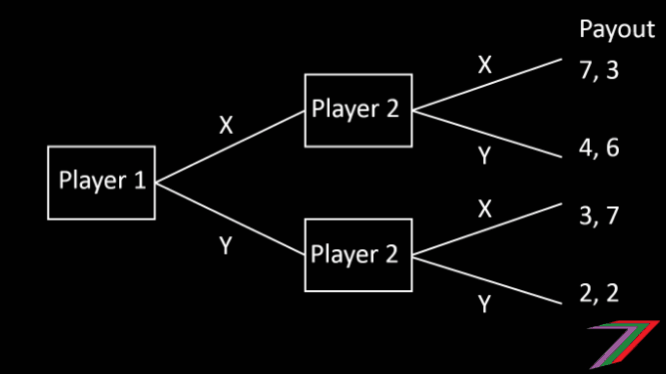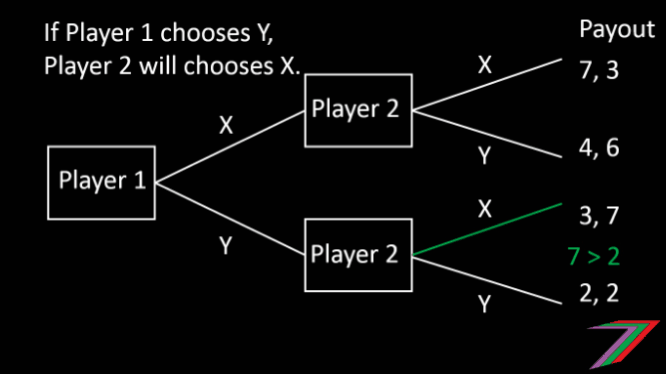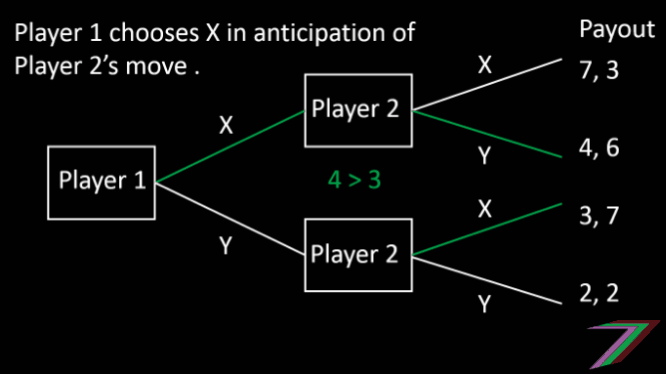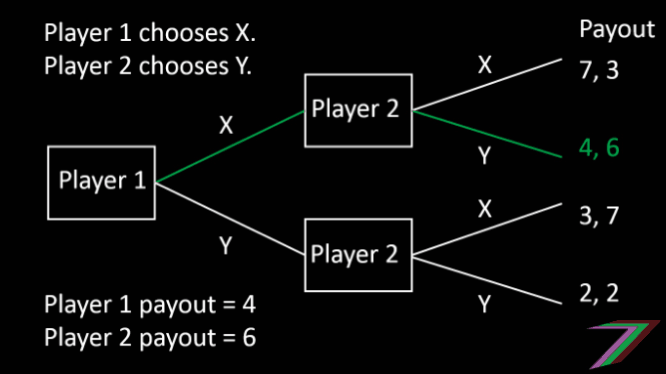
In the sequential game played above, Player 1 (first mover) can predict Player 2’s (second mover) selection and therefore, can achieve a higher payout.
Simultaneous games
In a simultaneous two player game, both players move at the same time. Neither player can observe the other player. If there is perfect information, it might be possible to predict what the other player will do. Simultaneous games can be most easily expressed in what is called the ‘normal form’. The normal form for a game is expressed like a matrix, see the table below.

In the above example, Player 1 is called the row player and Player 2 is called the column player. The first number in each box represents the payout to the row player (Player 1) and the second number presents the payout to the column player (Player 2).
The approach to determining the payouts for each player is different from the sequential game as Player 2 cannot observe Player 1 and Player 1 cannot directly predict Player 2’s selection. Instead, players will need to identify if they have a dominant strategy. A dominant strategy occurs when one selection always produces a better payout than any other selection regardless of what the other players do. Using the example, we can see that Player 1 has a dominant strategy. The payout from selecting X is always greater than the payout from selecting Y.
Player 2 does not have a dominant strategy. Therefore, the decision to select either X or Y is not initially clear. Player 2 should check if Player 1 has a dominant strategy. This is possible, if there is perfect information regarding Player 1’s payouts. Player 1, as mentioned earlier, has a dominate strategy, therefore will always select X. Player 2 now only needs to consider payouts that involve Player 1 selecting X. If Player 1 is only going to select X, Player 2 gets a higher payout by selecting Y.
Therefore, Player 1 will select X and Player 2 will select Y. The payout to Player 1 will be 4 and the payout to Player 2 will be 6. See the normal game presented below.

Repeated games
So far I have presented one-off games. In reality, most games repeat themselves to a certain extent. Repeated games can be a little more difficult to analyse than one-off games. This is especially so if there are an unknown number of rounds or the game has an infinite number of rounds. The repeated games are often referred to as rounds. There are many theories regarding the optimal approach to repeated games. Such theories include tit-for-tat, cooperation strategies, Nash mixed equilibrium, and other mixed equilibrium strategies. I will investigate these theories and approaches in later posts.

Real life application of game theory
So far this post has been very theoretical. Is game theory applied in the real world? Is game theory applied in any relevant way to the average person? The answer is ‘yes’ to all of the above.
Game theory can be applied to many different areas. These areas can range from business to social events. In regards to business, game theory can be used to help determine the optimal price for a product, the optimal amount to produce, the optimal amount of money to spend on advertising, the best audience to target. Insurance companies use game theory on a regular basis to influence their strategies. In regards to social events, game theory can be used to help us determine what gifts to buy people, what topics to focus on in conversations, what clothes to wear to occasions and basically anything that involves human interaction that could lead to different outcomes.
In a post I wrote in 2017, I discuss the application of game theory to dating. This post can be accessed using the link below.
Game theory can also be applied to bidding on Steemit bots. What is the optimal amount to bid? When is the optimal time to bid? Which bot should you bid on? The answers to these questions will depend on your objectives and your budget. Are you trying to make a profit? Are you trying to get your post high up on the hot or trending lists? Are you trying to get your post high up on a particular hot or trending list? Game theory can be used to help make those decisions. I will discuss how this can be done in a future post. So keep your eyes open for that.

Conclusion
This brings me to the end of my ‘Game Theory – Introduction’ post. I have many more posts to come in this series. I will explain the three most cited games of prisoner’s dilemma, chicken game and battle of the sexes. I will explain mixed equilibrium, Nash equilibrium, tit-for-tat, as well as first mover and second mover advantages. I will dedicate a post to explain how game theory can be applied to using Steemit bots.
Thank you for taking the time to read my post.











Really informative post about Game Theory, thanks for sharing :)
I am glad you enjoyed the post.
AGREED!!
game theory was definitely my favorite class/topic of economics in college. looking forward to the game theory post about upvote bots
Game theory is a very interesting topic. It allows us to be creative using mathematics. It can also be applied to so many areas. It is definitely worth learning about.
Awesome thanks for sharing! Would be wonderful to have a comprehensive understanding of bot logistics on STeemit.
The post will be more about applying strategies to bot voting.
So true...where are you from?
looking forward to your post on how to apply game theory to bot bidding
That post seems to be in high demand at the moment. It will be a fun one to write.
23.87% @pushup from @spectrumecons
It looks like a fun game, I think we should try it.
Go for it.
Thank you for sharing. Can't wait to follow the series. Well researched and beautifully presented.
Thank you @koheleth. There is a lot to come.
Sneaky Ninja Attack! You have been defended with a 25.87% vote... I was summoned by @spectrumecons! I have done their bidding and now I will vanish...Whoosh
This series is going to be amazing too waiting for more post's in this thanks a lot for sharing :)
No problem @blazing. I will be looking at game theory from many different angles.
Interesting theory. Real life is more complicated when it comes to apply a theory to it. You seem to look from every aspect though. Looking forward for bots.
Real life is certainly more complicated. Different parts of the theory apply at different times and sometimes other theories need to come in as well. Practice and experience are critical, theory is a good starting point.
I wish u had written dis piece late last year,it would have helped me alot in my operation research exams. I still appreciate ur write up today cos no knowledge is a waste.
Hopefully you can still make use of this information at some point.
good effort
Thank you @mrs.imran.
i am waiting for this type of post amazing
Thanks @mnaeemkhokhar. It is great that you enjoyed the content.
it seems that i've to be patient for your next post...
That's great that you are excited about it.
@originalworks
The @OriginalWorks bot has determined this post by @spectrumecons to be original material and upvoted it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
Thank you for sharing this @spectrumecons! I didn't have too much understanding of what Game Theory was and it's funny that I have stumbled upon this today as I was discussing it with a friend earlier.
Very informative and interesting so thank you again for sharing!
No problem @jeremyc. I am glad you found my post useful. Maybe the content can add to future discussions you have with your friend.
This is great, thanks!